ve a. - Educacional

1) Dois carros, A e B, em movimento retilíneo acelerado, cruzam um mesmo ponto em t = 0 s.
Nesse instante, a velocidade v 0 de A é igual à metade da de B, e sua aceleração a
corresponde ao dobro da de B.
Determine o instante em que os dois carros se reencontrarão, em função de v 0 e a.
2) Um menino, de massa igual a 40 kg, tenta, sem sucesso, empurrar uma caixa, de massa 80
kg, exercendo uma força horizontal de intensidade igual a 60 N.
a) Represente as demais forças que atuam na caixa e escreva quem exerce cada uma dessas
forças.
b) Calcule o módulo dessas forças.
3) Duas mesas de 0,80 m de altura estão apoiadas sobre um piso horizontal, como mostra a
figura a seguir. Duas pequenas esferas iniciam o seu movimento simultaneamente do topo da
mesa: 1) a primeira, da mesa esquerda, é lançada com velocidade V 0 na direção horizontal,
apontando para a outra esfera, com módulo igual a 4m/s; 2) a segunda, da mesa da direita, cai
em queda livre.
Sabendo que elas se chocam no momento em que tocam o chão, determine:
a) o tempo de queda das esferas;
b) a distância x horizontal entre os pontos iniciais do movimento.
4) O pêndulo balístico é um sistema utilizado para medir a velocidade de um projétil que se
move rapidamente. O projétil de massa m 1 é disparado em direção a um bloco de madeira de
massa m2, inicialmente em repouso, suspenso por dois fios, como ilustrado na figura. Após o
impacto, o projétil se acopla ao bloco e ambos sobem a uma altura h.
a) Considerando que haja conservação da energia mecânica, determine o módulo da
Página 1 de 11
velocidade do conjunto bloco-projétil após o impacto.
b) A partir do princípio da conservação da quantidade de movimento, determine a velocidade
inicial do projétil.
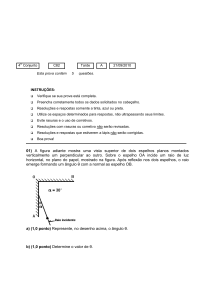
5) Um semáforo pesando 100 N está pendurado por três cabos conforme ilustra a figura. Os
cabos 1 e 2 fazem um ângulo α e β com a horizontal, respectivamente.
a) Em qual situação as tensões nos fios 1 e 2 serão iguais?
°
°
b) Considerando o caso em que α = 30 e β = 60 , determine as tensões nos cabos 1, 2 e 3.
°
Dados: sen 30 =
1
3
°
e sen 60 =
2
2
6) Um equilibrista se apresenta sobre uma bola, calibrada para ter uma pressão de 2,0 atm a
uma temperatura de 300K. Após a apresentação, essa temperatura elevou-se para 306K.
Considere desprezível a variação no volume da bola.
Calcule a pressão interna final da bola.
7) Um espelho côncavo de 50cm de raio e um pequeno espelho plano estão frente a frente. O
espelho plano está disposto perpendicularmente ao eixo principal do côncavo. Raios luminosos
paralelos ao eixo principal são refletidos pelo espelho côncavo; em seguida, refletem-se
também no espelho plano e tornam-se convergentes num ponto do eixo principal distante 8cm
do espelho plano, como mostra a figura.
Calcule a distância do espelho plano ao vértice V do espelho côncavo.
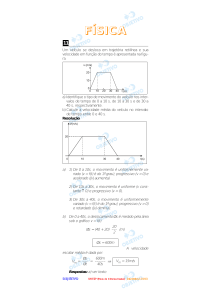
8) A figura representa o gráfico velocidade × tempo do movimento retilíneo de um móvel.
Página 2 de 11
a) Qual o deslocamento total desse móvel?
b) Esboce o gráfico posição × tempo correspondente, supondo que o móvel partiu da origem.
9) A figura ilustra um jovem arrastando um caixote com uma corda, ao longo de uma superfície
horizontal, com velocidade constante. A tração (T vetorial) que ele exerce no fio é de 20 N.
a) Desenhe todas as forças que atuam sobre o caixote, nomeando-as.
b) Calcule a força de atrito entre o caixote e o solo. São dados:
°
°
°
°
sen 37 = cos 53 = 0,6; sen 53 = cos 37 = 0,8.
10) Uma criança de 15 kg está sentada em um balanço sustentado por duas cordas de 3,0 m
de comprimento cada, conforme mostram as figuras (a) e (b) a seguir.
a) Qual a tensão em cada uma das duas cordas quando o balanço está parado [figura (a)]?
b) A criança passa a balançar de modo que o balanço atinge 0,5 m de altura em relação ao seu
nível mais baixo, [figura (b)]. Qual a tensão máxima em cada uma das duas cordas nesta
situação?
Página 3 de 11
11) Um para-quedista de 80 kg (pessoa + para-quedas) salta de um avião. A força da
resistência do ar no para-quedas é dada pela expressão:
2
F = - bV
onde b = 32 kg/m é uma constante e V a velocidade do para-quedista. Depois de saltar, a
velocidade de queda vai aumentando até ficar constante. O para-quedista salta de 2 000 m de
altura e atinge a velocidade constante antes de chegar ao solo.
a) Qual a velocidade com que o para-quedista atinge o solo?
b) Qual foi a energia dissipada pelo atrito contra o ar na queda desse para-quedista?
12) Uma partícula carregada eletricamente é lançada no interior de um campo magnético
uniforme de intensidade B, com velocidade de módulo V. A direção da velocidade é
perpendicular às linhas do campo magnético. Nestas condições, a partícula fica submetida a
uma força de intensidade F, expressa por F  q  V  B , onde q é o módulo em Coulombs (C)
da carga da partícula. A unidade B do Sistema Internacional é o Tesla.
Assim, o Tesla corresponde a:
13) A imagem de um objeto forma-se a 40 cm de um espelho côncavo com distância focal de
30 cm. A imagem formada situa-se sobre o eixo principal do espelho, é real, invertida e tem 3
cm de altura.
a) Determine a posição do objeto.
b) Construa o esquema referente à questão representando objeto, imagem, espelho e raios
utilizados e indicando as distâncias envolvidas.
14) Um objeto com 8,0 cm de altura está a 15 cm de uma lente convergente de 5,0 cm de
distância focal. Uma lente divergente de distância focal - 4,0 cm é colocada do outro lado da
convergente e a 5,0 cm dela.
Determine a posição e a altura da imagem final.
15) A figura abaixo ilustra um bloco de massa igual a 8 kg , em repouso, apoiado sobre um
plano horizontal. Um prato de balança, com massa desprezível, está ligado ao bloco por um fio
ideal. O fio passa pela polia sem atrito.
O coeficiente de atrito estático entre o bloco e a superfície é   0,2 . Dispõe-se de 4 pequenos
blocos cujas massas são:
m1  300 g
m2  600 g
m3  900 g
m4  1.200 g
Cada bloco pode ou não ser colocado no prato, de modo que o prato pode conter um, dois, três
ou até todos os quatro blocos. Considerando-se a aceleração da gravidade com valor igual a
Página 4 de 11
10 m / s2 , de quantas maneiras distintas é possível colocar pesos no prato, a fim de que o
bloco entre em movimento?
Página 5 de 11
Gabarito:
Resposta da questão 1:
No movimento uniformemente variado (MUV), a velocidade média é igual a média das
velocidades. Como podemos perceber nesta questão, as velocidades médias dos móveis A e B
são iguais (executam o mesmo deslocamento escalar no mesmo intervalo de tempo), portanto,
a média das velocidades dos dois veículos também será igual. Logo:
V0A  VFA V0B  VFB

2
2
V0A  (V0A  aA .t)  V0B  (V0B  aB .t)
2.V0A  aA .t  2.V0B  aB .t
Conforme o enunciado, temos:
V0A  V0 

V0B  2V0 

aA  a

aB  a / 2 
Assim:
2.V0  a.t  2.(2V0 )  (a / 2).t
a
2.V0  a.t  4.V0  .t
2
at
 2V0
2
4V0
t 
a
Resposta da questão 2:
a) Além da força Fm exercida pelo menino, atuam sobre a caixa o peso P, exercido pela
gravidade e a força Fs, exercida pelo solo. Esta última pode ser decomposta em uma
componente normal, N e uma tangencial, Fat.
b) | P | = mg = 80.10 = 800 N;
a
Se a caixa não se move, pela 1 Lei de Newton
Fx  0  Fat  Fm  60N
Página 6 de 11
F
y
 0  N  P  mg  400N
Assim, temos:
FS2  (Fat)2  N2  FS2  (60)2  (400)2  FS  404N
Resposta
da
1 2
a) S  gt  0,8  5t 2  t  0,4s
2
b) S  V.t  S  4  0,4  1,6m
questão
3:
Resposta da questão 4:
a) v1 =
2gh
b) v0 = [(m1+m2)/m1]
2gh
Resolução:
a) Após a bala ter atingido o bloco e comunicado-lhe uma velocidade o bloco oscila como um
pêndulo mantendo a energia mecânica conservada.
A figura mostra a situação.
1
MV 2  Mgh  V  2gh
2
b) A figura mostra as situações imediatamente antes e após a colisão.
Pela conservação da energia, vem:
Temos um sistema isolado de forças externas e podemos aplicar o Princípio da
Conservação da Quantidade de Movimento.
QTf  QTi  (m1  m2 )V  m1V0  V0 
(m1  m2 ) 2gh
m1
Página 7 de 11
Resposta da questão 5:
a) Para que T1 seja igual a T2 deve haver simetria e, portanto:   
b) Precisamos notar algumas detalhes:
 T3  P  100N
 T1 e T2 são ortogonais.
Passando dois eixos ortogonais com as direções dos cabos 1 e 2, podemos fazer a
decomposição mostrada na figura e aplicarmos as condições de equilíbrio de uma partícula.
T1  T3 cos   100  0,5  50N
T2  T3 sen  100 
3
 50 3N
2
Resposta da questão 6:
P0 .V0 P.V

n0 .T0
nT
P0 P
2,0
P
 

 P  2,04atm
T0 T
300 306
Resposta
da
questão
7:
d  8  8  25  d  9 cm
Resposta da questão 8:
a) 750 m
b) Observe o gráfico a seguir:
Página 8 de 11
Resposta da questão 9:
a) Observe a figura a seguir:
b) 16 N
Resposta da questão 10:
a) 75 N.
b) 100 N.
Resposta da questão 11:
a) 5,0 m/s.
6
b)1,6 . 10 J.
Resposta da questão 12:
[A]
Página 9 de 11
ma
F  qvB  ma  qVB  B 
 U(B) 
qV
kg
m
s2  kg
m
C.s
C
s
Resposta da questão 13:
1 1 1
a)  
f p p'
1
1 1
 
30 p 40
1
1
1
43



 p  120 cm
p 30 40 120
b)
Resposta da questão 14:
Imagem à 20/3 cm da lente divergente e com altura de 32/3 cm.
Resposta da questão 15:
Do ponto de vista da Matemática:
Seja P o peso total dos blocos que serão colocados no prato.
O sistema entrará em movimento se P  fat, ou seja,
P    N    PB  0,2  8  10  16 N.
Portanto, a soma das massas dos blocos que devemos colocar no prato deve ser maior do que
ou igual a 1600 g. Isso ocorre se colocarmos os blocos: 2 e 4; ou 3 e 4; ou 1, 2 e 3; ou 1, 2 e 4;
ou 1, 3 e 4; ou 2, 3 e 4; ou 1, 2, 3 e 4 (sete maneiras).
Página 10 de 11
Do ponto de vista da Física:
(Fat)max  μe .N  0,2x80  16N
m1 = 300 g  P1 = 3N
m2 = 600 g  P2 = 6N
m3 = 900 g  P3 = 9N
m4 = 1200g  P4 = 12N
Para haver movimento á preciso que
 P  16
As combinações possíveis são:
P1  P2  P3  18
P1  P2  P4  21
P2  P3  P4  27
P2  P4  18
P3  P4  21
Página 11 de 11