matemática 89 a 103 - Apostilas - Cantinho_do_professor

Visualização do documento
matemática 89 a 103.doc
(478 KB) Baixar
O TRANSFERIDOR
O transferidor é um instrumento que mede ângulos. Há variações dependendo do fabricante,
mas, em geral, ele apresenta uma volta completa de 360º (trezentos e sessenta graus) ou meia volta
de 180º. Os ângulos são medidos no sentido anti-horário (contrário aos ponteiros do relógio).
Observe a figura.
Há uma relação muito próxima entre a forma do transferidor e as representações de nosso
planeta. Veja as vistas da Terra, do espaço, e sua representação no globo de sua escola.
Em nosso dia a dia, superfícies circulares são muito comuns: relógios, espelhos, pratos, etc.
Além dos gráficos de barras e colunas, há os gráficos chamados “pizza” ou setores usados para
divulgar pesquisas. Eles podem ser construídos com o uso do transferidor.
Vamos praticar mais as medidas com esse instrumento tão importante. Procure manter
sempre o zero (0º) a sua direita.
 A linha que liga o centro da circunferência a qualquer ponto de seu contorno é chamada raio.
 A parte interior de uma circunferência limitada por raios é chamada setor circular.
 Observe os setores circulares marcados com letras.
D
C
A
B
a) Em quantas partes iguais a circunferência foi dividida? ________________
b) Quanto mede, em graus, cada setor? ______________
c) Qual o valor, em graus, da soma dos setores A e B? ___________
d) Qual o valor, em graus, da soma dos setores A, B e C? ___________
e) Qual o valor, em graus, da soma dos setores A, B, C e D? ___________
f) Pinte o setor A. Que fração da circunferência você pintou? ______________
g) Pinte o setor B. Que fração da circunferência está pintada agora? _________
h) Pinte o setor C. Que fração da circunferência está pintada agora? _________
i) Pinte o setor D. Que fração da circunferência está pintada agora? _________
 Observe os setores circulares da circunferência abaixo.
a) Quantos setores aparecem? _______
b) As medidas dos setores são todas
iguais? _________
c) Qual o maior setor? _________
d) Qual o menor setor? ______
D
B
A
C
e) Podemos afirmar que cada setor da circunferência acima representa ? __________
Justifique. ____________________________________________________________
____________________________________________________________
 Em cada divisão das circunferências, em setores iguais, leia, pinte a porção indicada e responda.
a) Quantos setores há? __________
b) Quanto mede cada setor? _______
c) Pinte três partes.
d) Que fração representa a parte pintada? ____
e) Quanto mede, em graus, o setor pintado?
_________
a) Quantos setores há? __________
b) Quanto mede cada setor? _______
c) Pinte quatro partes.
d) Que fração representa a parte pintada? ____
e) Quanto mede, em graus, o setor pintado?
_________
a) Quantos setores há? __________
b) Quanto mede cada setor? _______
c) Pinte nove partes.
d) Que fração representa a parte pintada? ____
e) Quanto mede, em graus, o setor pintado?
_________
a) Quantos setores há? __________
b) Quanto mede cada setor? _______
c) Pinte seis partes.
d) Que fração representa a parte pintada? ____
e) Quanto mede, em graus, o setor pintado?
_________
O relógio
A distância entre os números é medida em graus. Como a volta é de 360º, calculamos: 360º
 12 = 30º.
Logo cada número está exatamente distante 30º do outro.

Para utilizarmos bem o transferidor as primeiras marcações serão o centro e o 0º, localizado
à direita do medidor e situando o 90º para cima.
Usaremos o transferidor para representar um relógio na circunferência abaixo.
Escolha uma hora qualquer.
OBSERVAÇÃO: Repare que os ponteiros só apontam, exatamente, para os números
somente nas horas exatas.
 Marque o centro da circunferência observando a indicação no centro do instrumento.
 Comece a partir do 0º (zero graus) sempre da direita para a esquerda no sentido da seta.
CONSTRUINDO ÂNGULOS COM O TRANSFERIDOR
Pode-se construir ângulos a partir de um segmento de reta com o transferidor. É necessário
que se posicione o centro do medidor numa das extremidades do segmento e marque-se no sentido
anti-horário o ângulo desejado. Depois é só liga com um segmento de reta este ponto à
extremidade onde se encontrava o centro. Experimente.
a) Construa um ângulo de 30º posicionado o centro do transferidor na extremidade A.
Aproveite este momento e use sua régua. Qual a medida do segmento AB?
_______cm.
A
B
b) Construa um ângulo de 90º posicionado o centro do transferidor na extremidade A.
O tamanho do segmento AB mudou. Qual a medida agora? _______cm.
A
B
Agora você usará o transferidor para medir o ângulo formado pelos segmentos AB e AC.
Também deverá medir estes segmentos.
Medida do ângulo interno- ______
Medida de AB - ________
Medida de AC - ________
C
A
B
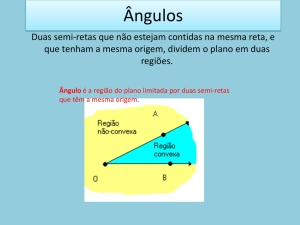
OS ÂNGULOS
Você já trabalhou com o transferidor para medir setores. Este instrumento é utilizado também
para medir ângulos de figuras planas. Observe as retas abaixo:
Reta r
abertura entre as retas
Reta s
Ângulo entre retas é a medida em graus (º) da abertura entre elas. No caso das figuras que
estudamos, podemos verificar os ângulos e descobrir muitas coisas.
Vamos medir alguns ângulos para você se familiarizar com o transferidor. Há no centro do
transferidor uma linha vertical que marca o centro. Posicionando esta linha sobre o vértice
(encontro de duas retas), poderá saber o ângulo. Observe o quadrado abaixo.
Os vértices do quadrado são representados pelas letras maiúsculas A, B, C e D.
Posicione o transferidor sobre o vértice C e verifique o ângulo marcado. Qual foi? ________
Faça o mesmo com os outros vértices.
A
B
C
D
O lado AC faz com o lado CD um ângulo de 90º. Este ângulo é chamado de reto. Os lados
AC e CD são chamados perpendiculares. Da mesma forma quando duas ruas se cruzam formando
um ângulo de 90º, dizemos que elas são perpendiculares.

Meça com o transferidor o ângulo de abertura entre as retas abaixo.
a) Qual foi o valor? ___________
b) O valor é menor que 90º ? __________
A

Meça o ângulo dos vértice C do paralelogramo e do vértice E do pentágono.
A
B
B
A
C
A
C
D
E
Valor do ângulo = ________
D
Valor do ângulo = ______
Quando um ângulo é menor que 90º ele é chamado de agudo e se ele é maior que 90º ele é
chamado de obtuso. O ângulo de 90º é chamado reto...
Arquivo da conta:
Cantinho_do_professor
Outros arquivos desta pasta:

CASA-DEF-TECNICO-2012-Rac.-Logico-Mat.-Zé-e-Edgar.pdf (1859 KB)
 apostila-de-desafios-matematicos-1.doc (1030 KB)
 apostila-de-desafios-matematicos-2.doc (718 KB)
 raciocc3adnio-lc3b3gico-matemc3a1tica-para-o-enem (1).pdf (73 KB)
 raciocc3adnio-lc3b3gico-matemc3a1tica-para-o-enem.pdf (73 KB)
Outros arquivos desta conta:


1º Bimestre
Atividades
 Curso_1
 Curso_2
 Curso_3
Relatar se os regulamentos foram violados








Página inicial
Contacta-nos
Ajuda
Opções
Termos e condições
Política de privacidade
Reportar abuso
Copyright © 2012 Minhateca.com.br