
Eletricidade
Corrente continua
Estática
(filme correntes estática)
Reação química
Pilhas
Baterias
Celdas de energia
2
Pilhas
3
Baterias
Corrente de carga
Corrente de flutuação
Corrente de equalização
Eletrolises
4
Célula de combustíveis
5
Corrente alterna
Lei de Faraday:
“Todo condutor mergulhado em um campo magnético variável terá em seus terminais uma fem
(força eletromotriz) induzida”.
e(t) = - N
d
dt
onde: N = número de espiras
d
= variação do fluxo magnético no tempo
dt
Lei de Lenz:
“A corrente que aparece em um circuito elétrico fechado, em função de uma fem (força
eletromotriz) induzida, tem sentido tal a anular a causa que lhe deu origem”.
6
Valor Instantâneo
V(t ) 2V0 Sent => Função senoidal
Valor de pico
Vp =
2Vo
Valor de pico a pico
Vpp = 2 2Vo
Valor médio
1
Vm =
2
2
2V0 Sent.dt
0
No caso da corrente alterna Vm = 0
Valor efetiva
Ve =
1
2
2
2
2V0 Sent dt
0
No caso da expressão apresentada para a tensão instantânea Ve = V 0
Tensão
Corrente
Resistência
Potência
7
Lei de Ohm
R=V/I
Leis de Kirchhoff
Porque utilizar corrente alterna
8
Correntes Parasitas ou Correntes de Foucault:
Transformadores de potencia
9
Tanque de expansão
Valvula de pressão
Termômetro
10
Manutenção de trafos de a oleo
11
Transformadores a seco
Transformadores de medição
Transformador de Potencial (TP)
Transformador de Corrente (TC)
12
Sistema trifásico de potencia
V1 2 * 220Sent
V1 2 * 2200
V2 2 * 220Sen[t 120]
V2 2 * 220120
V3 2 * 220Sen[t 240º ]
V3 2 * 220240
VAB [V1 V2 ] V1 2 * 2200
V1 2 * 2200
=> V1 2 * 220 cos t j * 2 * 220Sent
- V2 2 * 220120 => V2 2 * 220 cos t j * 2 * 220Sent
VAB [V1 V2 ] =
3 * 2 * 220 30
13
14
15
Conexão Triângulo (∆):
VL = VF
IL = IF .
3
Conexão Estrela (Y):
VL = VF .
3
IL = IF
Potencia trifásica em cargas equilibradas
16
Triangulo de potencias
Potência Aparente (S) [VA,KVA]
Potência Ativa (P):[ W.KW]
Potência Reativa (Q):[VAR,KVAR]
Questão 1
Nome do fabricante ...................................................................................................
Normas utilizadas .....................................................................................................
Numero de fases .......................................................................................................
17
Tipo de carcaça ( Frame) ...........................................................................................
Data de fabricação ....................................................................................................
Identificação do projeto do motor ( protocolos de fabricação) ..................................
Freqüência .................................................................................................................
Categoria de torque ..................................................................................................
Potencia (CV/Kw) .....................................................................................................
Rotação do motor ......................................................................................................
Fator de serviço ( sobrecarga) ...................................................................................
Classe de isolamento ...................................................................................................
Elevação de temperatura ............................................................................................
Relação entre a corrente de partida e a nominal .......................................................
Grau de proteção contra corpos sólidos ....................................................................
Grau de proteção contra líquidos ...............................................................................
Tensões de trabalho ...................................................................................................
Correntes de trabalho .................................................................................................
Regime de serviço .....................................................................................................
Máxima temperatura ambiente ..................................................................................
Altura máxima ............................................................................................................
Desenhe as conexões para 380 e 220V
....................................................................................................................
Numero dos rolamentos (abertos ou obturados) .........................................................
Tipo de graxa e quantidade ...........................................................................................
Peso do motor .............................................................................................................
Rendimento ................................................................................................................
Fator de potencia .......................................................................................................
18
Homologação ...............................................................................................................
19
20
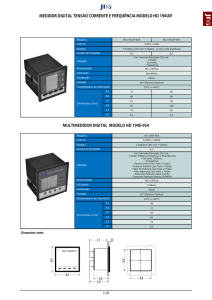
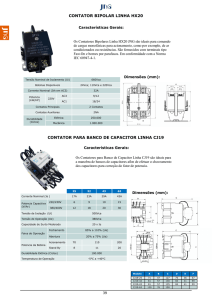
Plaquinha de Transformador de potencia
1.- Potencia
2.- Conexão delta para 13.8Kv
3.-Volume de óleo
4.-Diagrama fasorial
21
A impedância nos circuitos elétricos
Corrente no resistor
Ir =
V(t )
R
Corrente no capacitor ic C
Tensão no indutor
dV(t )
vL L
dt
di
dt
Aplicando a transformada de Laplace
Ir =
V(t )
R
/
=> Ir (s ) =
V( s)
R
=> R =
V( s )
Ir( s )
22
Ic = C
dV( t )
dt
VL L
/ => Ic (s ) = Cs V(s ) => Zc =
V( s )
I c(s)
=
1
1
1
=
=j = -j X c = X c 90
Cs
C
jC
di
/ VL ( s ) Lsi L ( s ) Z L Ls Lj X L 90
dt
Onde S = j e por sua vês 2f , no caso do Brasil f= 60Hz
No resitor
2
R1
1k
C1
150nF
L1
1640uH
V1
VOFF = 0
VAMPL = 10
FREQ = 10KHz
1
V
R3
100
R2
1k
R5
V
R4
100
0
10
4.71V
2.50V
0V
-2.50V
-4.94V
340us
V(R5:2)
350us
-v(R1:1)
360us
370us
380us
390us
400us
410us
420us
430us
440us
450us
460us
470us
480us
490us
500us
Time
No capacitor
2
R1
1k
C1V
150nF
L1
1640uH
V1
VOFF = 0
VAMPL = 10
FREQ = 10KHz
1
0
R5
R2
1k
R3
100
R4
100
V
10
23
7.2V
4.0V
(361.757u,6.2292)
(387.218u,6.6110)
0V
-4.0V
-8.0V
326.7us
340.0us
V(R3:1)
-V(C1:2)
360.0us
380.0us
400.0us
420.0us
440.0us
460.0us
480.0us
500.0us
520.0us
Time
No indutor
2
R1
1k
C1
150nF
L1 V
1640uH
V1
VOFF = 0
VAMPL = 10
FREQ = 10KHz
1
R3
100
R2
1k
R5
R4
100
0
V
10
6.90V
4.00V
(588.486u,6.3176)
(661.912u,6.5102)
0V
-4.00V
-7.63V
560.0us
V(R4:1)
580.0us
-V(L1:2)
600.0us
620.0us
640.0us
660.0us
680.0us
700.0us
720.0us
740.0us
758.9us
Time
Expressar as correntes em função do tempo e em forma fasorial
24
Valores Unitários (sistema por unidade)
O sistema "por unidade", ou, mais brevemente, sistema p.u., consiste na definição de valores de base para
as grandezas (tensão, corrente, potência, etc.), seguida da substituição dos valores das variáveis e constantes
(expressas no Sistema Internacional de unidades) pelas suas relações com os valores de base pré-definidos.
Exemplo 1:
Numa base de corrente Ib=50 A, a corrente I=30 A terá o valor I pu
I
30
0,6 pu
I b 50
Bases
Dadas as relações existentes entre as unidades só poderão definir-se duas bases independentes a partir das
quais se calculam todas as outras
Por sua vez, as bases de impedância e corrente calculam-se através das expressões:
S
Vb2
, I b b (caso monofásico)
Zb
Sb
Vb
Ib
Sb
3Vb
(caso trifásico)
Exemplo 2:
A reatância transitória de um alternador de 50 MVA, 10 kV é x'=12%. As bases da rede são, na zona
do alternador, Sb=100 MVA e Vb=11 kV.
Calcule seu valor em p.u. na nova base
1- Obtemos o valor na base atual
Vb2
10 2 K 2V 2
Zb
=
= 2 => X b1 = 0,12 x 2 = 0,24
50.000KVA
Sb
2- Calcular a nova base
Z b2
112 K 2V 2
= 1,21
100.000 KVA
25
3- Expressando o valor na nova base
X b2
0,24
0,198 PU
1,21
Exemplo 3:
A reatância de fugas (ou tensão de curto-circuito, Ucc) de um transformador de 30 MVA, 60/16 kV, é
xf=8%. A base de potência da rede é Sb=50 MVA, e as bases de tensão nas zonas do primário e
secundário são, respectivamente, Vbp=56,25 kV e Vbs=15 kV.
Encontre a expressão para a reatância em p.u. usando como base a rede
1 Encontrar o valor de base usado
Vb2
60 2 K 2V 2
=
= 120 => X f 1 = 0,08 x 120 = 9,6
Zb
30.000KVA
Sb
2- Calcular a nova base
Z b2
56,25 2 K 2V 2
= 63,28
50.000KVA
3- Expressando o valor na nova base
X f2
9,6
0,152 PU
63,28
O Autotransformador
O transformador analisado pressupõe isolação entre o primário e o secundário, existe uma outra
combinação entre as polaridades do transformador relacionando o primário com o secundário formando
um único bobinado. Esta outra disposição não só permite outras opções de tensões se não também um
aumento de potência.
26
Deve-se tomar cuidado com a corrente nas configurações abaixador e elevador.
Autotransformador como abaixador,
I2= I1 + Ic
Autotransformador como elevador
I1 = I2 + Ic
27
Jumbo de perfuração (dois braços)
Diagramas de corte
28
Tuneleras
29
Quedas Permitidas
Determine o triangulo de potencia do sistema
1 - Um jumbo de três braços opera com 4 trifásicos (380v), 2 motores de 30CV com fator de potencia de
0.8 , e 2 motores de 35CV de 0.7 esta afastado 330m da subestação a seção dos fios de alimentação é de
70mm.
a) Esta dentro das perdas permitidas?
b) Qual é a solução para este problema?
c) Qual seria o triângulo de potencias ideal para este caso?
d) Qual seria o valor do reativo necessário?
e) Qual é o valor do banco de capacitores?
f) Calcule o reativo para melhorar o fator de potencia a 0.92
30
Provinha 3
Nome: ...........................................................
1 Demonstre a relação entre a corrente de linha corrente de fase na lig delta
Demostre a relação entre a tensão de linha e a de fase na lig de estrela
2) Calcule os seguintes números complexo e os expresse na forma retangular:
3) Do circuito calcule a impedância equivalente
3) Uma capacitância de 3.53 μF e uma resistência de 40 Ω estão ligadas em série através de uma fonte CA
de 110V e 1.5 KHz. Calcule : Xc, Z, fase. I,Vr,Vc,Potencia
4.-Um motor em uma indústria possui uma impedância Z=4.2 +3.6jΩ, e é alimentado por uma tensão de
220V 60Hz, calcule:
A) As potências ativa, reativa e aparente
B) O fator de potência
31
C) O capacitor necessário para elevar o fator de potência para 1
5.- Para o circuito abaixo,
Calcule:
a) As potências ativa, reativa e aparente e o fator de potência do sistema.
b) Encontre a corrente total do circuito.
6.- De um transformador de 500VA de 220/24, seja isolado ou como autotrafo:
a). Quantas tensões podem ser obtidas
b). Qual é seu acréscimo de potencia
7 Considerando a tensão de referencia na cor verde, expresse os valores das três tensões no tempo e em
forma de fasor
7.2V
5.0V
(411.976u,6.2309)
(438.967u,6.3059)
(425.145u,4.5425)
0V
-5.0V
-9.5V
370us
V(R1:1)
380us
V(C1:1)
390us
V(L1:1)
400us
410us
420us
430us
440us
450us
460us
470us
480us
490us
Time
8 Calcule a impedância em Ω, de um transformador com uma impedância de 5.6/7.0% para o trafo de
10000/12500KVA e 69/39.8KV
9.- Que importância tem a polaridade magnética na operação de bancos de transformadores monofásicos e
motores elétricos CA?
10. Numa placa de características de um transformador se identifica: Dyn5, indique os tipos de conex~es do
primário, secundário e o desfasamento entre os bobinados primário e secundario
32
33






![I) Os ensaios de um transformador monofásico de 10 [kVA], 2.200](http://s1.studylibpt.com/store/data/000932973_1-0b7ab7de6203df074f1655674d08071c-300x300.png)



