2T + 1E

Resolução 2ºteste/1º exame 10/01/2017
EM RELAÇÂO ÀS PERGUNTAS TEÓRICAS INDICAM-SE APENAS OS TÓPICOS QUE
DEVERÃO SER ABORDADOS
1)
CONSIDERANDO QUE OS VALORES SÃO RETIRADOS DO GRÁFICO HAVERÁ SEMPRE ALGUMA IMPRECISÃO NOS
VALORES REFERIDOS
Um provete cilíndrico de uma liga de Alumínio, cujo comprimento e diâmetro iniciais eram, respectivamente,
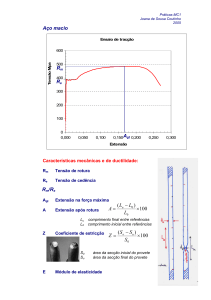
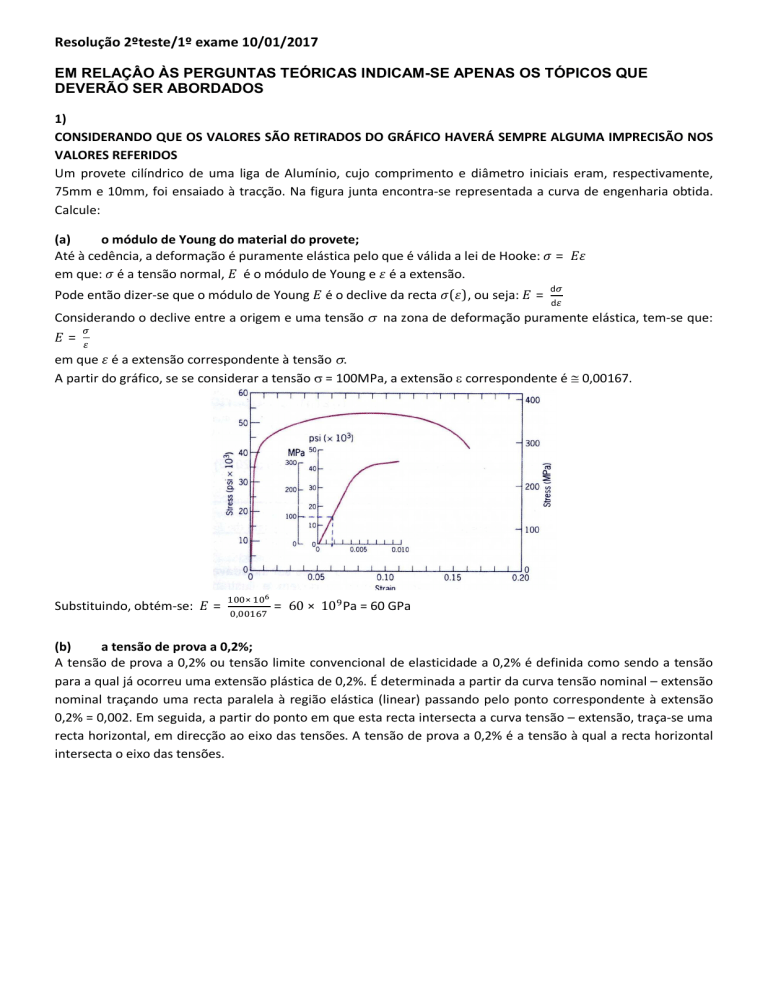
75mm e 10mm, foi ensaiado à tracção. Na figura junta encontra-se representada a curva de engenharia obtida.
Calcule:
(a)
o módulo de Young do material do provete;
Até à cedência, a deformação é puramente elástica pelo que é válida a lei de Hooke:
em que: é a tensão normal, é o módulo de Young e é a extensão.
Pode então dizer-se que o módulo de Young
é o declive da recta ( ), ou seja:
=
=
d
d
Considerando o declive entre a origem e uma tensão  na zona de deformação puramente elástica, tem-se que:
=
em que é a extensão correspondente à tensão .
A partir do gráfico, se se considerar a tensão  = 100MPa, a extensão  correspondente é  0,00167.
Substituindo, obtém-se:
=
×
,
= 60 × 10 Pa = 60 GPa
(b)
a tensão de prova a 0,2%;
A tensão de prova a 0,2% ou tensão limite convencional de elasticidade a 0,2% é definida como sendo a tensão
para a qual já ocorreu uma extensão plástica de 0,2%. É determinada a partir da curva tensão nominal – extensão
nominal traçando uma recta paralela à região elástica (linear) passando pelo ponto correspondente à extensão
0,2% = 0,002. Em seguida, a partir do ponto em que esta recta intersecta a curva tensão – extensão, traça-se uma
recta horizontal, em direcção ao eixo das tensões. A tensão de prova a 0,2% é a tensão à qual a recta horizontal
intersecta o eixo das tensões.
No caso em consideração obtém-se que a tensão de prova a 0,2% será  290MPa.
(c)
o alongamento do provete no instante em que a carga aplicada era 13345N;
Na figura apresenta-se a curva de engenharia (tensão nominal - extensão nominal), logo em primeiro lugar é
preciso calcular a tensão nominal correspondente à carga de 13345N.
A tensão nominal
N
é definida como sendo:
N
=
Força aplicada
Área inicial da secção recta
=
Uma vez que o provete era cilíndrico, a área inicial da secção recta seria:
em que
é o diâmetro inicial do provete, donde:
Substituindo, obtém-se:
N
=
×
×(
)
×
N
=
≅ 170 × 10 N/m = 170MPa
A partir do gráfico, se se considerar a tensão nominal
0,003.
N
Por definição a extensão nominal é: Extensão nominal =
pelo que o alongamento será: ∆ℓ = ℓ
=
= 170MPa, a extensão nominal correspondente é
N
=
Alongamento
Comprimento inicial
=
N 
∆ℓ
ℓ
N
Substituindo: ∆ℓ = 75 × 0,003 = 0,225mm
(d)
o diâmetro do provete ao atingir-se a tensão de 328MPa;
A partir do gráfico, obtém-se que a extensão nominal correspondente à tensão nominal
0,023.
N
= 328MPa, é
N 
Atendendo à definição de extensão nominal tem-se que o alongamento do provete será:
∆ℓ = 75 × 0,023 = 1,725mm
pelo que o comprimento do provete nesse instante será:
ℓ = 75 + 1,725 = 76,725mm
A tensão nominal N = 328MPa é superior á tensão de cedência logo já há deformação plástica. Durante a
deformação plástica pode considerar-se (desprezando a deformação elástica) que o volume se mantém constante
ou seja o volume num dado instante é igual ao volume inicial ( = ).
Por outro lado, a tensão nominal N = 328MPa é inferior á tensão de rotura (tensão máxima) logo a deformação
é uniforme, ou seja pode considerar-se que o volume é igual à área da secção recta do provete a multiplicar pelo
comprimento ( = × ℓ).
Uma vez que o provete é cilíndrico, a secção recta é circular e tem-se então que:
=
4
×ℓ =
=
4
×ℓ
em que
e ℓ são, respectivamente, o diâmetro e o comprimento iniciais do provete e
respectivamente, o diâmetro e o comprimento do provete no instante considerado.
Da equação anterior obtém-se:
=
×
e ℓ são,
ℓ
ℓ
Substituindo, obtém-se que o diâmetro do provete no instante em que a tensão aplicada é 328MPa, é:
= 10 ×
,
≅ 9,89mm
(e)
a tensão real aplicada ao provete nas condições referidas na alínea (d);
Conforme foi referido na alínea anterior, a tensão nominal N = 328MPa é inferior á tensão de rotura (tensão
máxima) logo a deformação é uniforme.
Enquanto a deformação for uniforme, é possível calcular a tensão real
N e da extensão nominal N utilizando a expressão: R = N (1 + N )
Nas condições referidas na alínea (d),
R
a partir dos valores da tensão nominal
N
= 328MPa e
R
= 328 × (1 + 0,023) = 335,5MPa
N
= 0,023, donde:
(f)
a carga aplicada ao provete no instante em que apareceu a estricção;
A estricção do provete surge no ponto de carga máxima.
A tensão máxima max (tensão de rotura) é a tensão nominal no ponto de carga máxima
max
=
max
max
ou seja:
em que
é a área inicial da secção recta. Logo:
max
=
max
em que
é o diâmetro inicial do provete. A tensão máxima
extensão nominal apresentada:
=
max
×
max
pode ser obtida da curva tensão nominal –
≅ 370MPa.
Substituindo, obtém-se: max = × (10 × 10 ) × 370 × 10 ≅ 29060N
Neste caso, obtém-se
max
(g)
o alongamento do provete ao atingir-se a tensão zero se ao atingir-se a tensão de 362MPa, o provete
tivesse sido descarregado.
A partir da curva tensão nominal – extensão nominal, obtém-se que a extensão nominal correspondente à tensão
nominal N = 362MPa, é N  0,06 à qual corresponde um alongamento ∆ℓ = 75 × 0,06 = 4,5mm.
Depois da cedência:
Alongamento (Δℓ) = Alongamento elástico (∆ℓel ) + Alongamento plástico (∆ℓpl ) 
∆ℓpl = ∆ℓ − ∆ℓel
Descarregamento  F = 0  Comprimento (ℓ) = Comprimento inicial (ℓ ) + ∆ℓpl  Δℓ = ∆ℓpl
Para calcular a extensão elástica
el , aplica-se
a lei de Hooke:
=
el

el
=
em que é o módulo de Young e é a tensão.
A extensão elástica el relaciona-se com o alongamento elástico por:
el
=
∆ℓel
ℓ
=
 ∆ℓel = ℓ
 ∆ℓpl = ∆ℓ − ℓ
Utlizando o módulo de Young calculado na alínea (a) ( = 60GPa), pode então calcular-se o alongamento do
provete ao atingir-se a tensão zero que será:
362 × 10
∆ℓ = ∆ℓpl = 4,5 − 75 ×
≅ 4,05mm
60 × 10
h) Indique quais os parâmetros extraídos deste ensaio que pode usar para caracterizar a rigidez e a resistência
mecânica.
A rigidez é avaliada pelo módulo de Young e a resistência mecânica pela tensão de cedência e pela tensão
máxima ou tensão de rotura.
2 ) a) Relativamente aos ensaios de impacto:
a1) dê uma definição sucinta;
DEFINIÇÃO ASTM: Um ensaio de impacto é um ensaio dinâmico realizado num determinado tipo de provete
entalhado, maquinado e rectificado superficialmente que é fracturado duma só vez por uma carga de impacto,
sendo medida a energia absorvida na rotura do provete. (Resposta sucinta).
(Pode-se também mencionar o seguinte: os valores de energia obtidos são comparações qualitativas para um
determinado provete e não devem ser convertidas em valores de energia a utilizar para efeitos de projecto. O
comportamento ao entalhe encontrado num determinado ensaio, aplica-se apenas ao tipo de provete,
geometria do entalhe e condições de ensaio envolvidas e não podem ser aplicadas a outros tipos de provetes e
condições de serviço.)
a2) destaque qual o seu objectivo;
Determinação da TENACIDADE, ie, genericamente, a energia que o material consegue absorver via deformação.
Esses ensaios:
-Medem a capacidade de absorção de energia via deformação plástica, a velocidades de deformação
elevadas (tipicamente 102 – 104 s-1)
-Constituem um método de comparação de materiais.
a3) indique quais os equipamentos que podem ser utilizados.
Geralmente, podem ser de dois tipos:
-Os que utilizam dispositivos pendulares ( métodos CHARPY e IZOD).
-Os que utilizam dispositivos de queda de massa.
b) Considere ensaios de impacto realizados a dois aços, de acordo com a mesma norma, a várias temperaturas:
aço estrutural A36 (aço de uso corrente na actualidade, por exº em construção civil) e aço usado no casco do
Titanic.
b1) Sabendo que a temperatura da água na zona do Atlântico Norte onde o Titanic se afundou era de -2 ºC,
identifique os materiais 1 e 2. Justifique sucintamente.
O material 1 é o aço A36 e o material 2 é o aço usado no casco do Titanic. Sabe-se que o Titanic afundou
visto que o material do casco estava muito abaixo da sua temperatura de transição dúctil-frágil. (Ou:
basta constatar que esse material tinha uma baixa resistência ao impacto a -2 ºC). Tendo o material um
comportamento eminentemente frágil, a energia absorvida no impacto é praticamente nula, como se vê
a -2 ºC no caso do material 2, ao passo que no caso do material 2 é de cerca de 40 J. Logo o material 2 é
certamente o aço usado no Titanic.
(Pode-se também mencionar o seguinte: Embora o ensaio em causa sirva essencialmente para fins
comparativos, vê-se que no caso do material 1 existe um valor apreciável de energia absorvida por impacto,
muito superior à do material 2 para essa temperatura. O facto do aço A36 ser usado de forma comum em
estruturas –edifícios, pontes- que frequentemente podem estar a operar nessa gama de temperaturas, aliado
ao facto de se saber que o Titanic não resistiu ao impacto a essa temperatura, sugere indubitavelmente que a
curva em causa do aço A36 só pode ser a 1. Dito de outra forma, se só tivéssemos estes 2 materiais para
operar a -2ºC em condições em que um carregamento de choque (ou impacto) é possível, o material a
seleccionar seria obrigatoriamente o 1.)
b2) Qual o objectivo de se realizarem ensaios de impacto a várias temperaturas?
Os metais são essencialmente dúcteis, mas em especial nos metais e ligas de estrutura ccc, existe uma faixa de
temperaturas relativamente pequena, na qual a energia absorvida cai apreciavelmente quando a temperatura
diminui. Nessa gama de temperaturas define-se a temperatura de transição dúctil-frágil (ttdf). É importante
identificar esse intervalo e em particular a ttdf, para prevenir a fractura frágil em materiais que supostamente
teriam em condições normais de operação, um comportamento dúctil. Nesse sentido, um tipo de ensaio em que
de forma expedita se podem fazer várias experiências em que se promove a fractura dum provete, variando a
temperatura, é o ensaio de impacto.
3) a) Um componente de um material está sujeito a um número de ciclos Nf = 108 até à fratura. Escreva a
equação que poderia aplicar para calcular a gama de tensões aplicada se o número de ciclos que a peça
suportaria até à fratura fosse de Nf = 107.
O número de ciclos é suficientemente elevado para se usar a lei de Basquin´s: ∆
=∆
b) Considere que um componente está sujeito a um número de ciclos até à fratura de 107 quando sujeita a um
carregamento cíclico por aplicação de uma tensão sinusoidal de amplitude
=110 MPa (stress range ou gama
de tensão ∆ = 220 MPa) com tensão média de 10 MPa, sendo a tensão de rotura ou tensão máxima de 250
MPa. Admitindo que b=0.1 qual a gama de tensão ∆ correspondente no caso de Nf =108?
Como a tensão média não é zero tem de se calcular
∆
=∆
Com ∆
∆
=
∆
=
= 229 MPa
= 229 MPa e N1f= 10 ciclos 
229 × (10 )
.
= ∆ (10 )
.
∆
= 181.9 MPa
c) Na caracterização mecânica de materiais frágeis, como os materiais cerâmicos, são mais usados os ensaios de
compressão do que os de tração. Explique porquê.
Duas razões:
-os materiais frágeis são difíceis de maquinar;
-a colocação destes materiais nas amarras de uma máquina poderia logo fracturar a peça.
d)
Pretende-se seleccionar o material adequado para uma barra cilíndrica sujeita a tracção. O
comprimento L0 é especificado e tem que suportar uma carga F sem alongar mais que um alongamento fixo . A
barra deve ser o mais leve possível. A área da secção transversal é a que for necessária. Elabore um quadro de
função, objectivo, constrangimentos, e variáveis livres.
Função
Barra à tracção
Constrang.
- Rigidez especificada
- Comprimento especificado
Objectivo
Minimizar a massa
Variáveis
livres
- Escolha do material
- Escolha da área da secção transversal
4)a) Indique o valor médio (aproximado) de Gc da alumina Al2O3.
Do gráfico tira-se que
=
≈ 4 MPa m1/2 e E=300 GPa, usando
=

= (42)/(300×103) = 5.33×10-5 ou 0.053 kJ/m2.
b) Calcule o tamanho máximo de um entalhe à superfície de uma amostra de Al2O3, considerando Y=1 e uma
tensão necessária para causar fratura de 1000 MPa.
com Y=1 e
= ∗
√
 4/1000 =√
 c=5.1×10-6 m
5) Considere o gráfico constante de desgaste ka em função da dureza H (em MPa).
a) Com base no gráfico indique em que intervalo se encontra a constante ka para o PTFE e calcule um
valor médio.
Do gráfico tira-se ka entre 8×10-7 e 3×10-6, calculando a média dá 1.9× 10-6 (1/MPa)
b) Faça uma estimativa da taxa de desgaste específica  no caso do material anterior em que se aplica
uma força normal de 10N numa área de 100 mm2.
Como  =
=
, substituindo valores obtém-se
 =1.9× 10-6 × (10/100) =1.9× 10-7
5c) Tendo em conta o gráfico anterior compare os metais com os polímeros em termos de capacidade
de resistência ao desgaste.
A taxa de desgaste específica Ω deve ser a menor possível. A capacidade de uma superfície resistir a uma pressão
de contacto é proporcional à sua dureza H
Nesta expressão aparecem duas “propriedades” materiais, ka e H. Um bom material para resistir ao desgaste terá
um baixo coeficiente K=kaH, pelo que os polímeros têm melhor resistência ao desgaste do que os metais.
6) a1) Descreva sucintamente cada um dos processos de fundição em molde de areia (sand casting) e de
fundição em molde (die casting).
O processo de fundição em molde de areia envolve várias etapas: em primeiro lugar faz-se um molde (em duas
partes) através da compactação de areia numa caixa. O molde tem a forma da peça pretendida. O molde é
fechado e vaza-se o metal líquido para dentro do molde. Após a solidificação abre-se o molde e retira-se a peça.
Na fundição em molde (die casting) o metal líquido é forçado a entrar num molde (die) de aço sob o efeito de
uma certa pressão. Após a solidificação o molde é aberto e a peça é retirada.
a2) Compare e enuncie as vantagens e desvantagens de cada um deles.
Ver acetatos das aulas teóricas.
Process
Advantage
Disadvantage
Sand casting
Die casting
Almost any metal, no size limit
Excellent dimensional accuracy,
high production rate
Wide tolerances, finishing required
Die cost high, size limited, usually
limited to nonferrous
a3) Qual dos dois processos permite produzir uma peça com uma superfície de menor rugosidade? Justifique.
Ver acetatos das aulas teóricas.
No processo de fundição em areia a peça fica mais rugosa do que na fundição em molde de aço, devido ao
contacto da peça com a areia ou com o molde metálico.
b)
Suponha que pretende produzir vários tubos poliméricos de comprimento elevado (10 metros) a partir
de grânulos desse mesmo polímero. Qual o processo que escolheria? Justifique.
Ver acetatos das aulas teóricas.
Dos vários processos de fabrico dos materiais poliméricos o que se aplica neste caso é a extrusão. Neste processo
o polímero na forma de grânulos é colocado sobre um parafuso que força o polímero a entrar num molde com
uma forma definida. É usado para produzir tubos, filmes e chapas.
c)
Classifique os processos indicados como A, B, C, D e E usando as designações: processo de forma
(shaping) primário, de forma secundário, de ligação e de acabamento/superfície.
A. Pultrusão – forma primário
B. Fabricação aditiva (aditive manufacturing) – forma primário
C. Soldadura (manual metal arc) - ligação
D. Anodização - acabamento
E. Hot isostatic pressure – forma primário
7) a) A energia total consumida por um produto tem 4 contribuições: materiais (materials), processamento
(manufacture), utilização (use) e reciclagem ou colocação em aterro (disposal). Compare qualitativamente
cada uma destas contribuições para a energia total, no caso de uma bicicleta a pedal e de um automóvel.
Ver acetatos das aulas teóricas.
A resposta pode ser dada com base nesta figura:
Materials
b) Diga o que entende por energia incorporada (embodied energy) e pegada de CO2 (CO2 footprint).
A energia incorporada de um material (ou embodied energy do inglês) Hm é a energia que é gasta para produzir
1kg desse material, em MJ/kg . A pegada de CO2 (ou CO2 footprint do inglês) é a libertação de CO2 para a
atmosfera que lhe está associada, em kg/kg.
8) a) A força de rotura FR de uma viga nestas condições é:
=
I×σR
=
com
b
×L
2
onde Z é uma constante dependente do modo de aplicação da força F, a largura e a espessura são iguais a b
(secção quadrada) e R a tensão de rotura do material, formule a expressão que permita seleccionar o material
que ofereça o menor custo para a mesma resistência.
Custo  VCm   ALCm   b 2 LCm
=
Como
Obtém-se
I×σR
=
com
b
×L
2
=
=
e
Substituindo
 C
 2m
 3
 R
Custo = L




 C
Menor custo => Menor  2m
 3
 R
b)

 => Maior


  23
 R
  Cm





Usando o mapa de Ashby abaixo desenhe 3 linhas para o projecto de menor custo correspondentes a:
=
=
=
1/2/Cm=C
2/3/Cm=C
/Cm=C
c) Usando o mapa de Ashby abaixo indique com uma seta a bolha do material que melhor satisfaz o critério da
alínea a). Indique claramente a recta que considerou.
2/3/Cm=C
9. Pretende-se seleccionar o material mais adequado para uma determinada aplicação em que se consideram
as quatro seguintes propriedades por ordem decrescente de importância (considere que as propriedades 3 e 4
têm a mesma importância).
a) O material a seleccionar é a liga de cobre.
Tensão máxima (MPa)
K (W m^-1 K^-1)
E (GPa)
Custo (euro/kg)
Tensão máxima (MPa)
0
0
0
0
K (W m^-1 K^-1)
1
0
0
0
E (GPa)
1
1
0
0,5
Custo (euro/kg)
1
1
0,5
0
PMMA
Liga Al
Liga Cu
Betão
Tensão máxima (MPa)
80
175
150
3
K (W m^-1 K^-1)
0,1
180
300
0,8
E (GPa)
3,5
70
120
20
Custo (euro/kg)
2,2
1,9
7,5
0,04
175,0000
3,0000
300
0,1
120
3,5
100
0,04
0,3333
max
K (W m^-1 K^-1)
0,0333
60,0000
100,0000
0,2667
0,0833
max
E (GPa)
2,9167
58,3333
100,0000
16,6667
0,0833
min
Custo (euro/kg)
1,8182
2,1053
0,5333
100,0000
1,0000
PMMA
Liga Al
Liga Cu
Betão
0,5000
max
Tensão máxima (MPa)
45,7143
100,0000
85,7143
1,7143
PMMA
Liga Al
Liga Cu
Betão
Tensão máxima (MPa)
22,8571
50,0000
42,8571
0,8571
K (W m^-1 K^-1)
0,0111
20,0000
33,3333
0,0889
E (GPa)
0,2431
4,8611
8,3333
1,3889
Custo (euro/kg)
0,1515
0,1754
0,0444
8,3333
Ind. Desemp
23,26
75,04
84,57
10,67
max
min
0,5000
0,3333
0,0833
0,0833
b) O material a seleccionar é o PMMA (embora com alguma reserva, pois o índice de desempenho da
liga de alumínio é praticamente igual).
Tensão máxima (MPa)
K (W m^-1 K^-1)
E (GPa)
Custo (euro/kg)
Tensão máxima (MPa)
0
0
0
0
K (W m^-1 K^-1)
1
0
0
0
E (GPa)
1
1
0
0,5
Custo (euro/kg)
1
1
0,5
0
PMMA
Liga Al
Liga Cu
Betão
Tensão máxima (MPa)
80
175
150
3
K (W m^-1 K^-1)
0,1
180
300
0,8
E (GPa)
3,5
70
120
20
Custo (euro/kg)
2,2
1,9
7,5
0,04
175,0000
3,0000
300
0,1
120
3,5
100
0,04
0,3333
min
K (W m^-1 K^-1)
100,0000
0,0556
0,0333
12,5000
0,0833
max
E (GPa)
2,9167
58,3333
100,0000
16,6667
0,0833
min
Custo (euro/kg)
1,8182
2,1053
0,5333
100,0000
1,0000
PMMA
Liga Al
Liga Cu
Betão
0,5000
max
Tensão máxima (MPa)
45,7143
100,0000
85,7143
1,7143
PMMA
Liga Al
Liga Cu
Betão
Tensão máxima (MPa)
22,8571
50,0000
42,8571
0,8571
K (W m^-1 K^-1)
33,3333
0,0185
0,0111
4,1667
E (GPa)
0,2431
4,8611
8,3333
1,3889
Custo (euro/kg)
0,1515
0,1754
0,0444
8,3333
Ind. Desemp
56,59
55,06
51,25
14,75
max
min
0,5000
0,3333
0,0833
0,0833
10) a1) o que é um aço inoxidável?
Um aço inoxidável é uma liga à base de Fe, com um mínimo de 11%Cr em solução para prevenir a corrosão e com
um teor de carbono reduzido.
a2) quais os tipos de ferros fundidos que existem?
CINZENTO, DÚCTIL (nodular), BRANCO e MALEÁVEL
a3) quais os requisitos de uma liga para ser usada numa pá de turbina a uma temperatura de 1200oC?
Resistência à fluência, à oxidação a alta temperatura, tenacidade, estabilidade térmica, resistência à fadiga, baixa
densidade.
b) Se a velocidade de deformação por fluência de um componente fabricado em aço 2¼ Cr-Mo não puder
exceder o valor de 10-8 s-1 a 600°C, qual será a tensão máxima admissível sem que ocorra dano nesse
componente à temperatura de 600°C? Considere uma lei exponencial para o regime de fluência estacionária e
os dados indicados na tabela. (R= 8,31 J mol-1K-1).
T=600+273=873K
̇ = ̇ 10
exp −
= 3.5 × 10 (
  = 97.1
MPa
) exp(−
×
.
∗
)