Questõesdedinâmica2

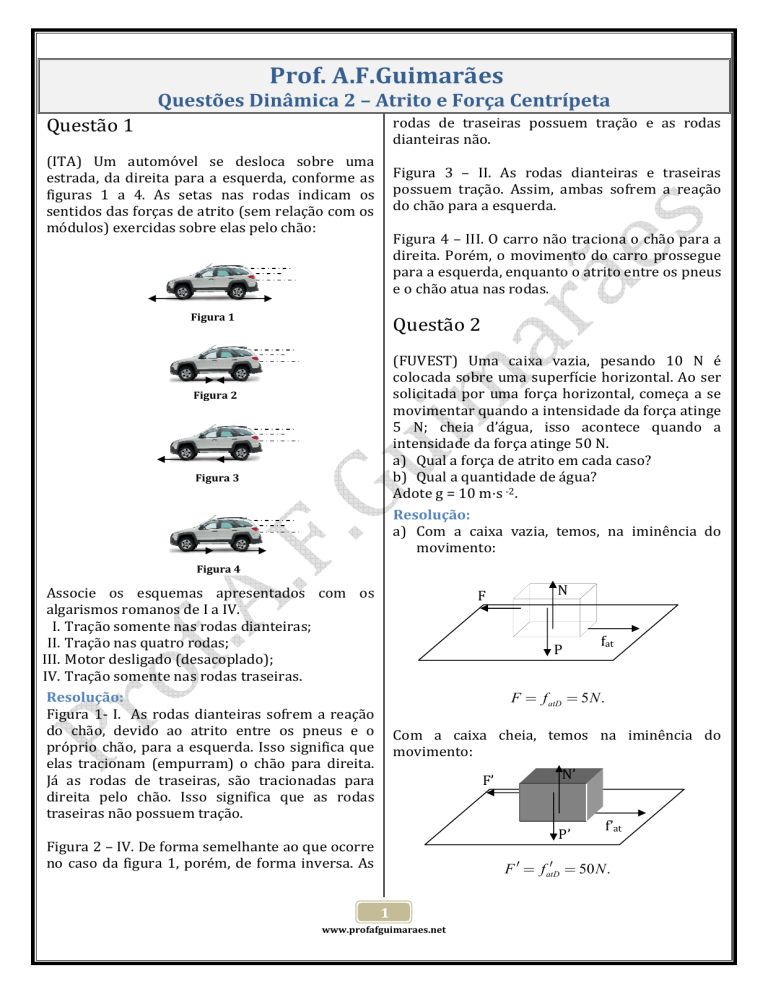
 Prof. A.F.Guimarães Questões Dinâmica 2 – Atrito e Força Centrípeta Questão 1 rodas de traseiras possuem tração e as rodas dianteiras não. Figura 3 – II. As rodas dianteiras e traseiras possuem tração. Assim, ambas sofrem a reação do chão para a esquerda. Figura 4 – III. O carro não traciona o chão para a direita. Porém, o movimento do carro prossegue para a esquerda, enquanto o atrito entre os pneus e o chão atua nas rodas. (ITA) Um automóvel se desloca sobre uma estrada, da direita para a esquerda, conforme as figuras 1 a 4. As setas nas rodas indicam os sentidos das forças de atrito (sem relação com os módulos) exercidas sobre elas pelo chão: Figura 1 Figura 2 Figura 3 Figura 4 Associe os esquemas apresentados com os algarismos romanos de I a IV. I. Tração somente nas rodas dianteiras; II. Tração nas quatro rodas; III. Motor desligado (desacoplado); IV. Tração somente nas rodas traseiras. Questão 2 (FUVEST) Uma caixa vazia, pesando 10 N é colocada sobre uma superfície horizontal. Ao ser solicitada por uma força horizontal, começa a se movimentar quando a intensidade da força atinge 5 N; cheia d’água, isso acontece quando a intensidade da força atinge 50 N. a) Qual a força de atrito em cada caso? b) Qual a quantidade de água? Adote g = 10 m s ‐2. Resolução: a) Com a caixa vazia, temos, na iminência do movimento: N F
fat P F = f atD = 5 N . Com a caixa cheia, temos na iminência do movimento: N’ F’
f’at P’ ′ = 50 N . F ′ = f atD
Resolução: Figura 1‐ I. As rodas dianteiras sofrem a reação do chão, devido ao atrito entre os pneus e o próprio chão, para a esquerda. Isso significa que elas tracionam (empurram) o chão para direita. Já as rodas de traseiras, são tracionadas para direita pelo chão. Isso significa que as rodas traseiras não possuem tração. Figura 2 – IV. De forma semelhante ao que ocorre no caso da figura 1, porém, de forma inversa. As 1 www.profafguimaraes.net b) Com a caixa vazia, podemos encontrar o coeficiente de atrito de destaque. Como a força normal de contato com o chão é igual ao peso, temos: f atD = µ N ⇒ 5 = µ10
∴ µ = 0,5.
O coeficiente de atrito não se altera pelo fato da caixa conter água. Assim, teremos: ′ = µ N ′ ⇒ 50 = 0,5 ⋅ N ′
f atD
∴ N ′ = 100 N .
Mas, N ′ = 10 + PH 2O . Assim, ∴ PH 2O = 90 N . Podemos escrever: Fy = Fsen530 = 20 ⋅ 0,8 = 16 N
Fx = Fcos530 = 20 ⋅ 0, 6 = 12 N .
Logo, N + Fy = P
Assim, Fr = Fx − f at
4a = 12 − 6 ∴ a =
(PUCCAMP) Um corpo de massa 4,0 kg está sobre uma superfície horizontal com a qual tem coeficiente de atrito dinâmico 0,25. Aplica‐se nele uma força F constante, que forma com a horizontal um ângulo de 530, conforme a figura. Se o módulo de F é 20 N e a aceleração local da gravidade é 10 m s ‐2, pode‐se concluir que a aceleração do movimento do corpo é, em m s ‐2: Dados: sen 530 = 0,8 e cos 530 = 0,6. G
F
530 A( ). 2,0; B( ). 1,5; C( ). 0,75; D( ). 0,50; E( ). 0,25. 3
m ⋅ s−2 = 1,5m ⋅ s−2 .
2
Letra “B”. Questão 4 (MACK) No sistema a seguir, o fio e a polia são ideais. Ao se abandonarem os blocos, A vai do ponto M para o N em 1,5 s. O coeficiente de atrito cinético entre o bloco A e a superfície de apoio é: A
M N 45cm
B
Dados: g = 10 m s ‐2, massa do bloco A, 8 kg e massa do bloco B, 2 kg. A( ). 0,1; B( ). 0,2; C( ). 0,3; D( ). 0,4; E( ). 0,5. G
F
Fy 530 N f at = µ N = 0, 25 ⋅ 24 = 6 N . Questão 3 Resolução: Ao ser abandonado, o bloco A percorre um at 2
espaço dado por: ∆S = v0t +
. Logo, 2
Fx P 2 www.profafguimaraes.net N = 40 −16 = 24 N .
Como Cerca de 9 kg (9 l) de água. Resolução: fat ∆S = v0t +
a (1,5)
at 2
2
2
0, 45 =
2
H=
H=
⇒ a = 0, 4m ⋅ s−2 .
h
sen α
( gsenα) t02
2
1
1 ⎛⎜ 2h ⎞⎟ 2
∴ t0 =
⋅⎜ ⎟
Essa é a aceleração do sistema. Essa aceleração é senα ⎜⎝ g ⎠⎟⎟
dada por Fr = PB − f atA . Assim, b) Se o bloco parte do repouso, sem as rodas, ele (mA + mB ) a = PB − f atA
desce com aceleração, dada por: 10 ⋅ 0, 4 = 20 − µ80 2
∴ µ = 0, 2.
a (2t0 )
h
=
2 senα
Letra “B”. 1
h
a=
⋅ 2.
2senα t0
Questão 5 Utilizando a expressão de t0, a aceleração será (FUVEST) Um bloco de massa m, montado sobre então dada por: rodas (para tornar o atrito desprezível), parte do repouso em A e leva o tempo t0 para atingir B. A /h
gsen 2α gsenα
massa das rodas é desprezível. Retirando‐se as . a=
⋅
=
2 senα
2/h
4
rodas, verifica‐se que o bloco, partindo do repouso em A, leva um tempo 2t0 para atingir B. Como a força resultante é igual à componente Px do peso menos a força de atrito. Teremos então: G
g
A ma = mgsenα − µ N , N = mgcosα
h α /gsenα
m
= mgsen
/⋅
/ / α − µmgcos
// α
B 4
3senα
a) Determinar o valor de t0. µ cos α =
4
b) Determinar o valor do coeficiente de atrito 3tgα
entre o plano e o bloco (sem rodas), em .
∴µ=
função de α. 4
Resolução: a) Desprezando o atrito, o intervalo de tempo Questão 6 que o carrinho leva para descer vale: (ITA) Dois blocos de massas m1 = 3 kg e m2 = 5 kg G
deslizam sobre um plano, inclinado de 600 com g
relação à horizontal, encostados um no outro, A com o bloco 1 acima do bloco 2. Os coeficientes h g senα α de atrito cinético entre o plano inclinado e os B blocos são µ1c = 0,4 e µ2c = 0,6, respectivamente para os blocos 1 e 2. Considerando a aceleração da gravidade g = 10 m s ‐2, a aceleração a1 do H bloco 1 e a força F12 que o bloco 1 exerce sobre o bloco 2 são, respectivamente: A( ). 6,0 m s ‐2; 2,0 N; 3 www.profafguimaraes.net B( ).
C( ).
D( ).
E( ).
mesma aceleração, ou seja, a1 = a2 = a. Assim, teremos: 8a = 69, 6 − 21
∴ a ≅ 6 m ⋅ s −2 .
Utilizando a equação para o bloco 1, teremos: 3⋅ 6,1 = 26,1− 6 − F12
F12 ≅ 2 N .
Letra “A”. 0,46 m s ‐2; 3,2 N; 1,1 m s ‐2; 17 N; 8,5 m s ‐2; 26 N; 8,5 m s ‐2; 42 N. Resolução: 1 2 600 N1 1 f
F21 at1 P1 N2 F12 2 fat2 P2 Para o bloco 1, teremos: Fr1 = Px1 − f at1 − F21
Questão 7 (ITA) Os blocos A e B da figura têm massas m. O coeficiente de atrito entre todas as superfícies é µ. A força F1 imprime ao bloco B da figura (I) velocidade uniforme. Calcule as relações F2/F1 e F3/F1, onde F2 é a força indicada na figura (II) e F3 é indicada na figura (III), para que o bloco B nessas figuras tenha velocidade constante. (I) A F1 B (II) A F2 B (III) A F3 B 3a1 = 30 sen600 − 0, 4 ⋅ 30 ⋅ cos 600 − F21 3a1 = 26,1− 6 − F12 .
Para o bloco 2, teremos: Fr 2 = Px 2 − f at1 + F12
Resolução: Figura (I): 0
0
5a2 = 50 sen60 − 0, 6 ⋅ 50 ⋅ cos 60 + F12 A F1 5a2 = 43,5 −15 + F12 .
B fatB Para que os blocos 1 e 2 desçam encostados, se faz necessário que os dois blocos tenham a Mas como a aceleração é nula, podemos escrever: 4 www.profafguimaraes.net A( ).
B( ).
C( ).
D( ).
E( ).
F1 = f atB = 2µ gm. Figura (II): fatBA F2 T A fatAB B fatB T = f atBA
F2 = f atAB + f atB , f atAB = µmg , f atB = 2µmg F2 = 3µmg.
Logo, F2 3µmg
=
= 1,5. F1 2µmg
Figura (III): fatBA F3 fatAB B fatB T f atBA = T = µmg
F3 = f atB + f atAB + T
F3 = 2µmg + µmg + µmg
F3 = 4µmg.
Logo, d D a < (d/D) µg; a > (d/D) µg; a >µg; a > (D/d) µg; a > [D/(D‐d)] µg; Resolução: A a
d
D Para que o vaso não caia, enquanto a extremidade A do forro percorrer “D”, o vaso percorrerá “D‐d”. Assim, teremos: at 2
∆S A = D =
2
1
⎛ 2 D ⎞⎟ 2
t = ⎜⎜ ⎟⎟ .
⎜⎝ a ⎠
Então, a aceleração do vaso será dada por: a′ ⎛ 2D ⎞
∆Svaso = D − d = ⋅ ⎜⎜ ⎟⎟⎟
2 ⎜⎝ a ⎠
a ′D
a=
.
D−d
Mas da força resultante no vaso, temos: FR = ma ′ = µmg
a ′ = µ g.
T A a F3 4µmg
=
= 2. F1 2µmg
Questão 8 (ITA) Um antigo vaso chinês está a uma distância d da extremidade de um forro sobre uma mesa. Essa extremidade, por sua vez, se encontra a uma distância D de uma das bordas da mesa, como mostrado na figura. Inicialmente tudo está em repouso. Você apostou que consegue puxar o forro com uma aceleração constante a (veja figura), de tal forma que o vaso não caia da mesa. Considere que ambos os coeficientes de atrito, estático e cinético, entre o vaso e o forro tenham o valor µ e que o vaso pare no momento que toca a mesa. Você ganhará a aposta se a magnitude da aceleração estiver dentro da faixa: 5 www.profafguimaraes.net Logo, a =
D
⋅ µ g. D−d
Questão 10 (UnB) Um disco gira em torno de seu centro, num plano horizontal, com uma velocidade angular ω = 5 rad s ‐1. Um pequeno corpo de massa m é colocado a uma distância r = 20 cm do centro do Questão 9 disco. Ache o menor coeficiente de atrito entre as (UNICAMP) Uma bola de massa 1,0 kg, presa à superfícies para o corpo não deslizar sobre o extremidade livre de uma mola esticada de disco. constante elástica k = 2000 N m ‐1, descreve um Resolução: movimento circular e uniforme de raio r = 0,50 m A força de atrito entre as superfícies deve ser a com velocidade v = 10 m s ‐1 sobre uma mesa resultante centrípeta sobre o corpo de massa m. horizontal e sem atrito. A outra extremidade da Assim, teremos: mola está presa a um pino em O, segundo a figura a seguir. f at = Fcp
mv
/ 2
, v = ωR
µmg
/ =
R
O ω 2 R 25 ⋅ 0, 20
G
=
µ=
v
10
g
∴ µ = 0,5.
a) Determine o valor da força que a mola aplica Letra “E”. na bola para que esta realize o movimento Questão 11 descrito. b) Qual era o comprimento original da mola (UnB) O trecho mais baixo de uma montanha‐
russa pode ser aproximado por um arco de antes de ter sido esticada? circunferência de raio R. Os ocupantes de um Resolução: a) Para que a bola realize o movimento descrito, carrinho, ao passar por este trecho, sentem uma a mola exerce sobre a bola uma força elástica sensação de aumento de peso. Avaliam que, no que aponta para o centro da trajetória do máximo, o seu peso foi duplicado. Desprezando movimento. Essa força elástica proporciona os efeitos de atritos, os ocupantes concluirão que a velocidade máxima atingida foi de: para a bola, uma resultante centrípeta. Logo: A( ). 3gR ; 2
mv
B( ). 3 gR ; Fel = Fcp =
R
C( ). 2 gR ; 2
1⋅10
Fel =
D( ). 2gR ; 0,5
gR . E( ).
∴ Fel = 200 N .
Resolução: No trecho mais baixo, a força normal de contato b) A deformação da mola neste caso vale: entre o ocupante com o acento do carrinho da montanha russa menos o peso do ocupante, será Fel = kx
a resultante centrípeta. 200 = 2000 x x = 0,1m.
Fcp = N − P, N = 2 P
mv
/ 2
Logo, como o raio da trajetória vale 0,5 m, o = mg
/ ∴ v = gR .
R
comprimento original da mola é de 0,4 m. 6 www.profafguimaraes.net Letra “E”. Questão 13 (FUVEST) Um carro percorre uma pista curva superelevada (tg θ = 0,2) de 200 m de raio. Desprezando o atrito, qual a velocidade máxima sem risco de derrapagem? g = 10 m ⋅ s−2
θ
A( ). 40 km h ‐1; B( ). 48 km h ‐1; C( ). 60 km h ‐1; D( ). 72 km h ‐1; E( ). 80 km h ‐1. Questão 12 (MACK) Na figura, o fio ideal prende uma partícula de massa m a uma haste vertical presa a um disco horizontal que gira com velocidade angular ω constante. A distância do eixo de rotação do disco ao centro da partícula é igual a 0,1 3 m . A velocidade angular do disco é (g = 10m s ‐2) m 600 A( ). 3 rad s ‐1; B( ). 5 rad s ‐1; Resolução: C( ). 5 2 rad s ‐1; Para que não ocorra risco de derrapagem, vamos D( ). 8 3 rad s ‐1; considerar apenas as forças peso e normal de E( ). 10 rad s ‐1; contato com a pista. Vamos decompor a força Resolução: normal de contato com a pista e assim encontrar Vamos, a partir da resultante centrípeta, suas componentes. A componente na direção determinar as componentes da tração do fio. E horizontal será a resultante centrípeta e a com as componentes da tração, determinaremos componente vertical equilibrará o peso. a velocidade angular. Ty N Ny 600 θ Tx Fcp P
Nx θ
Tx = Fcp ⇒ Tsen600 = mω 2 R
P 0
Ty = P ⇒ Tcos 60 = mg .
Da figura podemos concluir que: −2
Onde R = 0,1 3 m e g = 10 m ⋅ s . Agora, mv 2
dividindo a primeira equação pela segunda, e N
F
Nsen
=
⇒
θ
=
x
cp
R utilizando tg 600 = 3 , teremos, então: N y = P ⇒ Ncos θ = mg.
2
0
2
/ 60
m
ω 0,1 3
Tsen
/ ω 0,1 3
=
⇒ 3=
0
Onde R = 200 m. Agora dividindo a primeira / 60
Tcos
10m
10 /
equação pela segunda, e utilizando a tg θ, ∴ ω = 10rad ⋅ s−1.
teremos, então: 7 www.profafguimaraes.net mv
/ 2
/
Nsen θ
v2
200
=
⇒ tg θ =
/ cos θ
N
10m
2000
/
0, 2 ⋅ 2000 = v 2 ∴ v = 20m ⋅ s−1
−1
Letra “D”. v = 72km ⋅ h .
Questão 14 R
N Ny Nx α h P Onde R = h ⋅ tgα . Dividindo a primeira equação pela segunda teremos: /
mg
Nsen
gh ⋅ tgα
α
/
, v = ωR
= 2 ⇒ tg α =
/
Ncos
v2
α mv
/
R
/ ⋅ tg α
1
gh
g
tg α = 2 /2 2 ∴ h = 2 ⋅ 2
ω tg α
ω h tg α
(ITA) Uma massa pontual se move, sob a influência da gravidade e sem atrito, com velocidade angular ω em um círculo a uma altura h 0 na superfície interna de um cone que forma um ângulo α com seu eixo central, como mostrado na figura. A altura h da massa em relação ao vértice do cone é: α h g
A( ).
; ω2
g ⎛⎜ 1 ⎞⎟
⎟ ; B( ).
⋅⎜
ω 2 ⎜⎝ sen α ⎠⎟⎟
h=
g
⋅ cotg 2 α.
2
ω
Letra “D”. Questão 15 (ITA) Um aro metálico circular e duas esferas são acoplados conforme ilustra a figura abaixo. As esferas dispõem de um furo diametral que lhes permite circular pelo aro sem atrito. O aro começa a girar, a partir do repouso, em torno do diâmetro vertical EE’, que passa entre as esferas, até atingir uma velocidade angular constante ω. g ⎛⎜ cotg α ⎞⎟
Sendo R o raio do aro, m a massa de cada esfera e ⎟⎟ ; C( ).
⋅⎜
2 ⎜
desprezando‐se os atritos, pode‐se confirmar ω ⎝ sen α ⎠⎟
que: g
2
D( ).
; ⋅
cotg
α
E ω ω2
E( ). Inexistente, pois a única posição de R equilíbrio é h = 0. m m Resolução: Vamos determinar as componentes da força E’ normal de contato nas direções horizontal e vertical. Assim, teremos: A( ). As esferas permanecem na parte inferior do aro porque esta é a posição de mínima energia N y = P ⇒ Nsen α = mg
potencial. 2 B( ). As esferas permanecem a distâncias r de mv
N x = Fcp ⇒ Ncos α =
.
EE’ tal que, se 2θ for o ângulo central cujo vértice R
é o centro do aro e cujos lados passam pelo centro das esferas na posição de equilíbrio 8 www.profafguimaraes.net baixo. Dessa forma, a componente vertical não se equilibraria com o peso. Letra “B”. ω 2r
, estando as esferas g
abaixo do diâmetro horizontal do aro. C( ). As esferas permanecem a distâncias r de EE’ tal que, se 2θ for o ângulo central cujo vértice é o centro do aro e cujos lados passam pelos centros das esferas na posição de equilíbrio ω 2r
, estando as esferas estável, então tg θ =
g
acima do diâmetro horizontal do aro. D( ). As alternativas (B) e (C) anteriores estão corretas. E( ). A posição de maior estabilidade ocorre quando as esferas estão nos extremos de um mesmo diâmetro. estável, então tg θ =
Questão 16 (IME) Uma mesa giratória tem velocidade angular constante ω, em torno do eixo y. Sobre esta mesa encontram‐se dois blocos, de massas m e M, ligados por uma corda inelástica que passa por uma roldana fixa à mesa, conforme a figura a seguir. Considerando que não existe atrito entre a mesa e o bloco M, determine o coeficiente de atrito mínimo entre os dois blocos para que não haja movimento relativo entre eles. Considere d a distância dos blocos ao eixo de rotação. Despreze as massas da roldana e da corda. Dado: M>m y
ω
m M d Resolução: Para uma posição de equilíbrio estável, teremos que, as componentes da força normal de contato nas esferas, nas direções vertical e horizontal, respectivamente, resultam no equilíbrio com o peso e na resultante centrípeta nas esferas. Assim, teremos: E ω
R N R Ny θ Nx r P E’ N x = Fcp ⇒ Nsen θ = mω 2 r
N y = P ⇒ Ncos θ = mg.
Resolução: y ω T m fatmM fatMm
T M d Onde r = Rsen θ . Agora dividindo a primeira equação pela segunda, teremos então: Como não deve haver movimento relativo entre as massas m e M, os dois blocos são submetidos à /
Nsen
θ m
/ ω 2r
mesma aceleração centrípeta, dada por: =
/
Ncos
θ
mg
/
v2
ω 2r
a
=
= ω 2d. cp
∴ tg θ =
.
d
g
Acima da horizontal, a força normal de contato nas esferas estaria apontando na diagonal para 9 www.profafguimaraes.net Onde v é a velocidade linear dos centros dos objetos com relação ao eixo y. Assim, para os corpos, teremos: FcpM = T + f atmM ⇒ Macp = T + µmg
Fcpm = T − f atMm ⇒ macp = T − µmg .
Vamos multiplicar a segunda equação por ‐1 e somá‐las. Assim, teremos: Macp = T + µmg
−macp = −T + µmg
( M − m) acp = 2µmg ( M − m) ω 2 d
∴µ=
2mg
.
10 www.profafguimaraes.net