franchi_cmgg_me_sjrp

Propaganda

Universidade Estadual Paulista “Júlio de Mesquita Filho”
Instituto de Biociências, Letras e Ciências Exatas
Claudia Maria G. Gonçalves Franchi
Orientador: Prof. Dr. Manoel Ferreira Borges Neto
Ensaio sobre o Fluxo de Ricci e os Buracos Negros: Fundamentação e
Estudo Computacional
São José do Rio Preto - SP
Fevereiro/2013
Universidade Estadual Paulista “Júlio de Mesquita Filho”
Instituto de Biociências, Letras e Ciências Exatas
Programa de Pós-Graduação em Ciência da Computação
Departamento de Ciência da Computação e Estatı́stica
Ensaio sobre o Fluxo de Ricci e os Buracos Negros: Fundamentação e
Estudo Computacional
Claudia Maria G. Gonçalves Franchi
Orientador: Prof. Dr. Manoel Ferreira Borges Neto
Dissertação como parte dos requisitos para
obtenção do tı́tulo de Mestre em Ciência
da Computação, junto ao Programa de PósGraduação em Ciência da Computação, Área
de Concentração - Computação Cientı́ﬁca, do
Instituto de Biociências, Letras e Ciências
Exatas da Universidade Estadual Paulista
“Júlio de Mesquita Filho”, Campus de São
José do Rio Preto.
São José do Rio Preto - SP
Fevereiro/2013
Franchi, Claudia Maria G. Gonçalves.
Ensaio sobre o ﬂuxo de Ricci e os buracos negros: fundamentação e
estudo Computacional / Claudia Maria. G. Gonçalves Franchi. - São
José do Rio Preto: [s.n.], 2013.
126 f. : il. ; 30 cm.
Orientador: Manoel Ferreira Borges Neto
Dissertação (mestrado) - Universidade Estadual Paulista, Instituto de
Biociências, Letras e Ciências Exatas
1. Computação - Matemática. 2. Relatividade geral (Fı́sica) 3. Buracos Negros (Astronomia) 4. Fluxo de Ricci. I. Ferreira Neto, Manoel
Borges. II. Universidade Estadual Paulista, Instituto de Biociências,
Letras e Ciências Exatas. III. Tı́tulo.
CDU - 519.67
Ficha catalográﬁca elaborada pela Biblioteca do IBILCE
Campus de São José do Rio Preto - UNESP
CLAUDIA MARIA G. GONÇALVES FRANCHI
Ensaio sobre o Fluxo de Ricci e os Buracos Negros: Fundamentação e Estudo
Computacional
Dissertação apresentada como parte dos
requisitos para obtenção do tı́tulo de Mestre
em Ciência da Computação, área de Computação Cientı́ﬁca junto ao Programa de
Pós-Graduação em Ciência da Computação
do Instituto de Biociências, Letras e Ciências
Exatas da Universidade Estadual Paulista
“Júlio de Mesquita Filho”, Campus de São
José do Rio Preto.
BANCA EXAMINADORA
Prof. Dr. Manoel Ferreira Borges Neto
UNESP - São José do Rio Preto - SP
Orientador
Prof. Dr. Carlos Roberto Valêncio
UNESP - São José do Rio Preto - SP
Prof. Dr. Wladimir Seixas
UFSCAR - Universidade Federal de São
Carlos - SP
São J. do R. Preto, 20 de Fevereiro de 2013
Ao meu adorado esposo Vander, ele sabe o
por quê.
“Somente nas misteriosas equações do amor é
que alguma lógica ou razão pode ser encontrada”. Só estou aqui agora por sua causa.
Você é a razão de eu existir. “Você é toda a
minha razão”.
John Nash
Agradecimentos
À Deus, que me carregou quando me faltaram forças.
Ao querido Vander Franchi, meu grande parceiro e incentivador, o qual não tenho
palavras para agradecer tudo o que abdicou por mim.
Aos meus ﬁlhos adorados, Ana Jéssica e Raul Cézar, pelo carinho, paciência e
compreensão, nunca se esqueçam de que vocês sempre serão a minha maior criação e o
meu mais perfeito projeto.
Ao Prof. Dr. Borges, por ser minha inspiração, pela orientação, pela oportunidade
de trabalhar ao seu lado e pela conﬁança em mim depositada, a qual guardarei com
carinho pelo resto dos meus dias, jamais me esquecerei das nossas conversas.
Ao Renato Gomes dos Reis, meu grande amigo, pela contribuição no desenvolvimento deste trabalho, por não me deixar desistir e por acreditar em mim quando eu
mesma não acreditei.
Aos meus alunos, por me permitirem partilhar da sua jornada e por me ensinarem
tanto, quando deveriam apenas aprender.
Aos funcionários, docentes e discentes do Departamento de de Pós Graduação em
Ciência da Computação da Unesp; À Grazielle, à Kelly e à Maria Angélica, do Departamento de Engenharia de Alimentos, pelas revisões, pelas sugestões e por todo o apoio
durante o desenvolvimento do trabalho.
Aos colaboradores, professores, funcionários e proprietários da Tecmed e da Unilago, pela oportunidade e pela conﬁança, instituições que me ampararam e me permitiram
crescer, serei-lhes eternamente grata.
ii
Então Einstein estava errado quando disse:
“Deus não Joga Dados”. Considerando os buracos negros, sugere não só que Deus joga dados, mas que às vezes nos confunde jogandoos onde eles não podem ser vistos.
Stephen Hawking.
Resumo
A curvatura de Ricci desempenha um papel importante em relatividade geral, em que é o
termo dominante nas equações de campo de Einstein. Sendo assim, no presente trabalho
pretende-se: (i) Desenvolver e aplicar técnicas de ﬂuxo de Ricci à Teoria da Relatividade
Geral (TRG); (ii) Discorrer sobre as propriedades do espaço-tempo utilizando superfı́cies
mergulhadas; (iii) Utilizar simulações computacionais em assuntos pertinentes à teoria da
Relatividade Geral, particularmente ao estudo dos Buracos Negros e sua evolução. Para
R para simulações utilizando elementos geométricos
tal, utilizar-se-á a plataforma Maple do ﬂuxo de Ricci, pois esta consiste numa importante ferramenta, já que é uma plataforma
integrada, que pode realizar computação simbólica, numérica e visualizações no mesmo
ambiente. Pode-se assim realizar todos os passos necessários para as simulações numéricas
R
no ﬂuxo de Ricci utilizando o software Maple .
Esta aplicação pode se tornar uma
opção importante a ser adotada, constituindo assim numa base conﬁável para outros futuros trabalhos.
Palavras-chave: Computação Matemática, Relatividade Geral, Fluxo de Ricci, Buracos negros.
Abstract
The Ricci curvature plays an important role in general relativity, where is the dominant
term in Einstein’s ﬁeld equations. Thus, the present work aims to : (i) Develop and apply
Ricci ﬂow techniques to the General Theory of Relativity (TRG); (ii) Discuss the properties of spacetime using layered surfaces; (iii) Using computer simulations in matters
pertaining to the theory of General Relativity, particularly the study of black holes and
R for simulations using
their evolution. To this end, It will use the platform Maple geometric elements of the Ricci ﬂow, because this is an important tool, since it is an integrated platform, that can perform symbolic computation, numerical and views in the same
environment. One can thus carry out all the steps necessary for numerical simulations in
R . This application can become an important option
Ricci ﬂow using software Maple to be adopted, thus providing a reliable basis for other future work.
Keywords: Mathematical Computing, General Relativity, Ricci Flow, Black holes.
Sumário
Lista de Figuras
x
1 Introdução Geral
1
1.1
Objetivos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
1.2
Descrição dos Capı́tulos . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
2 Deﬁnição e histórico dos Buracos Negros
4
3 Estrutura matemática dos buracos negros
14
3.1
Introdução . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
3.2
Buraco negro de Schwarzschild . . . . . . . . . . . . . . . . . . . . . . . . . 15
3.3
Buraco negro de Kerr . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
3.4
Espaço Tempo de Minkowski . . . . . . . . . . . . . . . . . . . . . . . . . . 18
4 Termodinâmica dos Buracos Negros
25
4.1
A mecânica dos buracos negros . . . . . . . . . . . . . . . . . . . . . . . . 28
4.2
As leis da mecânica dos buracos negros . . . . . . . . . . . . . . . . . . . . 28
4.3
4.2.1
Lei Zero . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
4.2.2
Primeira Lei . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
4.2.3
Segunda Lei . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
4.2.4
Terceira Lei . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
Conjectura da Censura Cósmica . . . . . . . . . . . . . . . . . . . . . . . . 35
4.3.1
Versão Fı́sica da Conjectura da Censura Cósmica . . . . . . . . . . 36
4.3.2
Formulação Fı́sica da Conjectura da Censura Cósmica . . . . . . . . 36
4.4
Topologia dos Buracos Negros . . . . . . . . . . . . . . . . . . . . . . . . . 37
4.5
Teorema da Área . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
v
vi
4.5.1
Demonstração do Teorema da Área dos Buracos Negros . . . . . . . 39
5 Aspectos quânticos dos buracos negros
5.1
42
Radiação de Hawking . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
5.1.1
Processo de Emissão de Radiação . . . . . . . . . . . . . . . . . . . 47
6 O Fluxo de Ricci
52
6.1
Introdução . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
6.2
O Fluxo de Ricci e outros Fluxos Geométricos . . . . . . . . . . . . . . . . 53
6.3
Teorema de Gage-Hamilton . . . . . . . . . . . . . . . . . . . . . . . . . . 54
6.4
Deﬁnição matemática do ﬂuxo de Ricci . . . . . . . . . . . . . . . . . . . . 57
6.5
Fluxo de Ricci normalizado . . . . . . . . . . . . . . . . . . . . . . . . . . 58
6.6
Exemplos de soluções exatas do Fluxo de Ricci - Variedades de Einstein . . 58
6.7
Fluxo de Ricci de forma geométrica . . . . . . . . . . . . . . . . . . . . . . 60
6.8
6.7.1
Caso bidimensional . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
6.7.2
Caso tridimensional: Neck Pinch . . . . . . . . . . . . . . . . . . . 60
6.7.3
Neck Pinch degenerado . . . . . . . . . . . . . . . . . . . . . . . . . 62
6.7.4
Deﬁnição de ε-Neck . . . . . . . . . . . . . . . . . . . . . . . . . . 64
6.7.5
Sóliton . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
Generalização do ﬂuxo de Ricci . . . . . . . . . . . . . . . . . . . . . . . . 67
R
7 Visualizações com o Maple 70
7.1
R
Software Maple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
7.2
R para visualização de
Utilização do Maple variedades regulares . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
7.2.1
7.3
Variedades regulares . . . . . . . . . . . . . . . . . . . . . . . . . . 71
Visualizações com o ﬂuxo de Ricci . . . . . . . . . . . . . . . . . . . . . . . 75
8 Resultados e discussões
8.1
8.2
80
Buraco Negro de Schwarzschild . . . . . . . . . . . . . . . . . . . . . . . . 80
8.1.1
Métricas: Codiﬁcação por Vierbein . . . . . . . . . . . . . . . . . . 82
8.1.2
Métricas Codiﬁcadas por Vierbein . . . . . . . . . . . . . . . . . . . 82
Exemplo de Solução e Plotagem dos Gráﬁcos . . . . . . . . . . . . . . . . . 84
8.2.1
Parabolóide de Flamm . . . . . . . . . . . . . . . . . . . . . . . . . 86
vii
8.3
Buraco Negro de Kerr . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90
8.3.1
8.4
Exemplo de Solução e Plotagem dos Gráﬁcos - Buraco Negro de Kerr 90
A esfera colapsante . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94
9 Considerações Finais
98
9.1
Sugestão para Trabalhos Futuros . . . . . . . . . . . . . . . . . . . . . . . 99
9.2
Produção de trabalhos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99
Referências Bibliográﬁcas
102
Lista de Figuras
2.1
Diagrama HR teórico mostrando as diversas fases da evolução de uma estrela de 5 massas
solares, a partir da seqüência principal (SP), no extremo esquerdo inferior, e quanto tempo
a estrela leva em cada fase, segundo os cálculos de Icko Iben Jr. (1931-) [19]. . . . . . . .
2.2
8
Esquema de evolução estelar, não em escala, para massas diferentes. A classiﬁcação espectral de uma estrela na sequência principal com 0,45 MSol é M1V, 8 MSol é B2V, 10 MSol
é B1V e 25 MSol é O7V [19]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3
9
Ilustração da Nasa mostra um buraco negro supermassivo no centro da galáxia em espiral
NGC 1365. Este buraco tem 2 milhões de vezes a massa do Sol. [19]. . . . . . . . . . . . .
13
3.1
Diagrama Carter-Penrose do espaço tempo de Minkowski de [41]. . . . . . . . . . . . . . .
19
3.2
Representação de um espaço tempo resultante do completo colapso gravitacional de um
corpo esférico de [25], [33]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3
Um diagrama de acordo com o mesmo espaço-tempo ﬁgura 3.2. Neste caso a região α do
espaço tempo fı́sico está do lado de fora de J − (I+ ) [43]. . . . . . . . . . . . . . . . . . . .
3.4
20
20
Outra possı́vel representação do fecho de M do espaço tempo fı́sico que fora representado pictoricamente na ﬁgura anterior. Como na ﬁgura 3.3, as dimensões angulares são
suprimidas, desta forma um ponto determinado deste diagrama representa uma 2-esfera
(excetuando-se r = 0 e i0 ) - Diagrama de Penrose [45]. . . . . . . . . . . . . . . . . . . . .
3.5
Ilustração: Em (a) : y x curvas do tipo temporal. Em (b), pontos no cojunto aberto de
b também estão em I + + (x) ∩ I − (y), em (c) de acordo com teorema 3.1 [43]. . . . . . . .
4.1
21
23
Ilustração de uma singularidade nua e uma singularidade oculta por um horizonte de
eventos (adaptada de [41]). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
37
4.2
Ilustração das hipersuperfı́cies de Cauchy. . . . . . . . . . . . . . . . . . . . . . . . . . . .
38
4.3
Representação esquemática de pontos conjugados, de [25]. . . . . . . . . . . . . . . . . . .
39
4.4
Ilustração dos pontos conjugados em um espaço-tempo bibimensional de [34]. . . . . . . .
39
4.5
Ilustração da formação de um buraco Negro de colapso gravitacional esfericamente simétrico
4.6
- diagrama de Finkelstein [25], [41], [58]. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
40
Diagrama de Finkelstein ilustrando a colisão de dois buracos negros [58]. . . . . . . . . . .
41
viii
ix
5.1
Ilustração onde se observa que em (A) o par forma-se e desaparece sem atravessar o horizonte, em (B) o par forma-se do lado de fora e ambas as partı́culas atravessam o horizonte
e em (C) o par forma-se do lado de fora mas apenas uma das partı́culas atravessa o horizonte. 46
5.2
Ilustração representando a Linha de Corte no Plano-v Complexo. . . . . . . . . . . . . . .
6.1
Ilustração de uma curva fechada parametrizada e seus respectivos vetores de curvatura
(curvatura de Gauss) [79]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.2
49
54
Ilustração que mostra um cı́rculo encolhendo sob o ﬂuxo de redução da curva (todos os
cı́rculos são concêntricos mas, estão dispostos paralelamente para facilitar a visualização
de [79]). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.3
Ilustração que mostra uma elı́pse encolhendo sob o ﬂuxo de encurtamento da curva e por
ﬁm, se tornando cada vez mais semelhante a um circulo de [79]. . . . . . . . . . . . . . . .
6.4
55
Caso bidimensional da esfera S 2 , com uma ilustração demonstrando que, regiões onde
K < 0, tendem à se expandir e regiões onde K > 0, tendem à colapsar [73]. . . . . . . . .
6.5
55
60
Caso tridimensional da esfera S 2 , com uma ilustração demonstrando que, regiões onde
K < 0, tendem à se expandir e regiões onde K > 0, tendem à colapsar [73]. . . . . . . . .
61
6.6
Ilustração de como a métrica evolui contraindo assim a secção transversal S 2 [73]. . . . .
62
6.7
Ilustração da ampliação da curvatura, em que se pode observar o neck pinch se alongando
e limitado por uma esfera S 2 [73]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.8
Ilustração apresentando uma 3-esfera assimétrica em que, em L, a região tende a se expandir e em R, a região tende a colapsar [73]. . . . . . . . . . . . . . . . . . . . . . . . . .
6.9
62
62
Representação de uma 3-esfera assimétrica, ilustrando que R colapsou até se tornar um
pequeno ponto que no ﬂuxo do tempo tende a desvanecer [73]. . . . . . . . . . . . . . . .
63
6.10 Ilustração onde se pode observar a formação de uma singularidade [73]. . . . . . . . . . .
63
6.11 Ilustração onde se pode observar a formação de um neck pinch degenerado [73]. . . . . . .
63
6.12 Ilustração da ampliação do neck pinch degenerado, onde se pode observar um soliton de
Bryant [73]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
64
6.13 Ilustração da secção transversal de uma 2-esfera com curvatura escalar próxima a 1 [2]. .
65
6.14 Ilustração onde observa-se a evolução do ε-neck [2]. . . . . . . . . . . . . . . . . . . . . . .
65
7.1
R - versão 13. . . . . . . . . . . . . . . . . . . . .
Ilustração da tela de abertura do Maple
71
7.2
Gráﬁco de uma semicircunferência construı́da utilizando-se o software Maple. . . . . . . .
72
7.3
Gráﬁco uma esfera construı́da utilizando-se o software Maple. . . . . . . . . . . . . . . . .
73
7.4
Curva Espacial construı́da utilizando-se o software Maple. . . . . . . . . . . . . . . . . . .
73
7.5
Gráﬁco de um paraboloide construı́do utilizando-se o software Maple. . . . . . . . . . . .
74
7.6
Gráﬁco de uma circunferência construı́da utilizando o software Maple. . . . . . . . . . . .
75
7.7
Gráﬁco de um toro construı́do utilizando-se o software Maple . . . . . . . . . . . . . . . .
75
8.1
Uma n-esfera é uma generalização da superfı́cie de uma esfera ordinária em uma dimensão
arbitrária. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
88
x
8.2
Paraboloide de Flamm, com a topologia com topologia R × S 1 , (cilindro topológico). O
buraco negro de Schwarzschild é um reﬂexo da geometria de Schwarzschild normal. Não
há buraco branco, apenas um buraco negro e seu reﬂexo [95]. . . . . . . . . . . . . . . . .
89
8.3
Gráﬁco do Buraco negro de Schwarzschild, gerado pelo software Maple. . . . . . . . . . .
89
8.4
Gráﬁco do buraco negro de Kerr, gerado pelo software Maple. . . . . . . . . . . . . . . . .
94
8.5
Gráﬁco ilustrando uma 2-Esfera Colapsante, vista em corte [93]. . . . . . . . . . . . . . .
96
8.6
R
Gráﬁco de uma Esfera Colapsante construı́da no software Maple .
. . . . . . . . . . . .
96
Capı́tulo 1
Introdução Geral
Richard Hamilton, nascido em 1943, investigava a natureza intrı́nseca de variedades
em três dimensões, desenvolveu o ﬂuxo de Ricci, que é utilizado pelos matemáticos para
entender a topologia de variedades em dimensão três [1], [2], e pode ser aplicado no
estudo de teorias geométricas, como a Teoria da Relatividade Geral. Hamilton, utilizou
os trabalhos de Eells e Sampson [3] sob os quais se ediﬁca um estudo sobre problemas
pertinentes às Conjecturas de Poincaré e Smith, culminando posteriormente na completa
elaboração do programa de Geometrização de Thurston [4], utilizada para descrever os
modelos cosmológicos.
Este trabalho tem como objetivo o desenvolvimento de um método quantitativo,
a partir de simulações utilizando métodos geométricos aproveitando as caracterı́sticas
R que relacione
geométricas do ﬂuxo de Ricci, realizadas com adjutório do software Maple ,
o ﬂuxo de Ricci à teoria da Relatividade Geral, particularmente ao estudo dos buracos
negros e sua evolução. Deﬁnida uma variedade riemanniana com tensor métrico gij ,
(M, gij ) pode-se calcular o tensor de Ricci Rij , que contém informações sobre as médias
das curvaturas seccionais em uma espécie de ”traço” do tensor de curvatura de Riemann.
Considerando-se o tensor métrico e o tensor de Ricci associados, funções da variável tempo,
o ﬂuxo de Ricci pode ser deﬁnido pela equação de evolução geométrica.
∂t gij = −2Rij .
(1.1)
O ﬂuxo de Ricci normalizado faz sentido para variedades compactas e é dado pela
equação:
∂t gij = −2Rij +
2
Ravg gij
n
(1.2)
CAPÍTULO 1. INTRODUÇÃO GERAL
1.1
2
Objetivos
Visando evidenciar a aplicabilidade ao estudo dos buracos negros, considera-se a
variedade riemanniana assintoticamente plana e tridimensional. Deﬁnem-se os buracos
negros como as regiões do espaço-tempo a partir da qual escapar para o inﬁnito é impossı́vel e, portanto, referem-se a uma estrutura assintótica. Exige-se que a métrica tenda a
uma métrica plana ﬁxa δij no inﬁnito,
gij → δij + 0 (1/r).
(1.3)
Dada a métrica inicial gij , o ﬂuxo de Ricci evolui com a métrica, consoante ao
seu tensor de Ricci. A evolução do parâmetro t e da famı́lia de métricas em (M, gij (t))
satisfazem a equação de ﬂuxo de Ricci, Equação 1.1. O problema de simulações utilizando
métodos geométricos e visualizações com o ﬂuxo de Ricci em variedades de dimensões três
decorrem naturalmente da natureza geométrica deste ﬂuxo, que atua diretamente sobre a
métrica da superfı́cie, tendendo a não preservar o mergulho. Joachim Hyam Rubinstein e
Robert Sinclair [5] obtiveram uma série de resultados através da restrição às classes das
métricas de revolução, pois tais simetrias são preservadas sob a ação do ﬂuxo de Ricci e
a métrica depende consideravelmente de um número menor de parâmetros em tais casos.
Estas superfı́cies tendem a permanecer mergulhadas em R3 tornando a visualização direta
possı́vel.
É possı́vel também utilizar simulações numéricas já constante em outros trabalhos e realizadas com adjutório de softwares, fazer uso de mecanismos já utilizados na
Relatividade Numérica, uma vez que as simulações numéricas para o ﬂuxo de Ricci são
análogas.
1.2
Descrição dos Capı́tulos
Objetivando clareza na exposição dos assuntos, o presente trabalho encontra-se
dividido em nove capı́tulos.
No segundo capı́tulo, sucintamente, serão expostos alguns conceitos sobre a história
dos buracos negros, desde as primeiras teorias até os trabalhos ﬁnais envoltos nesta teoria
tão fascinante.
No terceiro capı́tulo será apresentada a estrutura matemática dos buracos negros,
CAPÍTULO 1. INTRODUÇÃO GERAL
3
o buraco negro de Schwarzschild, o buraco negro de Kerr, cujas métricas serão posteriormente utilizadas para a visualização.
O quarto capı́tulo é dedicado à termodinâmica dos buracos negros, as lei da
mecânica dos buracos negros e sua analogia com a termodinâmica são o principal enfoque do capı́tulo.
Em seguida, no quinto capı́tulo, serão tratados os aspectos quânticos dos buracos
negros e a radiação de Hawking.
O sexto capı́tulo será dedicado ao ﬂuxo de Ricci, inicialmente será tratado do ﬂuxo
de Ricci e demais ﬂuxos geométricos, deﬁnição do ﬂuxo de Ricci e exemplos de soluções
exatas do ﬂuxo de Ricci, ﬁnalizando com as variedades de Einstein em seguida o ﬂuxo
de Ricci será tratado em sua forma geométrica. Serão tratados os casos bidimensional e
tridimensional, Neck Pinch, ε-Neck, e sobre os sólitrons; culminando com a generalização
do ﬂuxo de Ricci.
R e sua utilização
No capı́tulo sete faz-se uma introdução sobre o software Maple para visualização de superfı́cies mergulhadas.
O capı́tulo oito é reservado aos resultados e discussões sobre as métricas dos buracos
negros de Schwarzchild e de Kerr.
No capı́tulo nove, trata-se as considerações ﬁnais e sugestões para trabalhos futuros.
Capı́tulo 2
Deﬁnição e histórico dos Buracos
Negros
Segundo Laplace (1798), “Inúmeras estrelas apresentam em sua coloração e em
seu brilho variações periódicas muito notáveis; existem algumas que aparecem de súbito
e outras que desaparecem, depois de terem, durante algum tempo, emitido uma luz muito
viva. Que prodigiosas mudanças devem se operar na superfı́cie desses corpos, para que eles
sejam tão sensı́veis à distância que nos separa; de quanto eles devem ultrapassar aquelas que nós observamos na superfı́cie do Sol! Todos esses corpos se tornam invisı́veis no
mesmo lugar onde foram observados, pois eles em nada mudaram durante o seu aparecimento; existem, portanto, nos espaços celestes, corpos obscuros tão consideráveis, e talvez
tão grandes em número, como as estrelas. Um astro luminoso de mesma densidade que a
Terra, e cujo diâmetro fosse o do Sol, não deixaria, em virtude de sua atração, que nenhum de seus raios luminosos nos atingissem; é possı́vel que os maiores corpos luminosos
do universo sejam por isso mesmo invisı́veis. Uma estrela que, sem possuir tal grandeza,
ultrapasse consideravelmente o Sol, provocaria uma sensı́vel redução na velocidade da luz
e aumentaria assim a extensão de sua aberração”. [6]
A expressão “buraco negro” foi adotada em 1969 pelo cientista americano John
Wheeler [6], como descrição gráﬁca de uma ideia que, retrocedendo pelo menos duzentos
anos, chega a um tempo em que haviam duas teorias sobre a luz: segundo Isaac Newton,
a luz era composta por partı́culas, a outra dizendo que a luz se formava por ondas.
De acordo com a dualidade onda/partı́cula da mecânica quântica, as duas teorias estão
CAPÍTULO 2. DEFINIÇÃO E HISTÓRICO DOS BURACOS NEGROS
5
corretas, sendo que, a luz pode ser considerada tanto onda como partı́cula. Segundo a
teoria de que a luz é formada por ondas, não ﬁca estabelecido o fato de ela responder à
gravidade. Mas se a luz é composta por partı́culas, pode-se esperar que ela seja afetada
pela gravidade. Inicialmente, acreditava-se que as partı́culas da luz se deslocavam em
velocidade inﬁnita, de tal modo que a gravidade jamais seria capaz de atraı́-las. Porém,
a descoberta de Ole Roemer, um astrônomo dinamarquês, de que a luz se propaga em
velocidade ﬁnita, implica num efeito importante [7].
Com base nessa suposição em 1783, John Michell, postulou que, “uma estrela com
massa suﬁcientemente compacta poderia ter um campo gravitacional tão forte que a luz
não poderia escapar. Qualquer luz emitida pela superfı́cie da estrela seria puxada de volta
por uma atração gravitacional antes que conseguisse se afastar”. Michell sugeriu ainda
que deveria haver um grande número de estrelas nessa situação. Ainda que não fosse
possı́vel observá-las, pois sua luz não atingiria os olhos humanos, poderı́a-se sofrer uma
atração gravitacional [7]. Esses objetos são os chamados atualmente de buracos negros,
pois são vácuos escuros no espaço. Decerto não é consistente tratar a luz com a teoria
de Newton sobre a gravidade, uma vez que a velocidade da luz é ﬁxa. No entanto,
uma teoria adequada que justiﬁque como a gravidade atua sobre a luz só foi sugerida
por Einstein [8, 9, 10] em 25 de novembro de 1915, em um seminário onde, comunicou as
equações ﬁnais da Teoria da Relatividade Geral para a Academia de Berlim. Mesmo assim,
decorreu um longo perı́odo antes que as implicações da teoria para estrelas compactas
fossem compreendidas.
Em 1915, Karl Schwarzschild [11] encontrou entre 08 de novembro e o ﬁm do ano,
um mês após a publicação da “Teoria da Relatividade Geral” de Einstein, a ”Solução
de Schwarzschild”. Foi a primeira solução exata para as equações de campo de Einstein
executando-se a solução trivial para o espaço plano. Nas coordenadas de Schwarzschild,
a métrica poderia ser expressa como [11]:
2
ds = c
2
2GM
1− 2
cr
2GM
dt − 1 − 2
cr
2
−1
dr2 − r2 dΩ2 ,
(2.1)
em que, G corresponde a constante de gravitação universal, M é entendida como a massa
do objeto e, dΩ2 = dθ2 + sin2 θ2 dφ, corresponde a um elemento de ângulo sólido. A
constante rs =
2GM
c2
é entendida como raio de Schwarzschild e desempenha uma função
CAPÍTULO 2. DEFINIÇÃO E HISTÓRICO DOS BURACOS NEGROS
6
importante na solução de Schwarzschild.
A métrica de Schwarzschild é a solução para as equações de campo gravitacional no
vácuo, válida apenas externamente ao corpo em questão. Portanto, em um corpo esférico
de raio R, a solução é válida para r > R. Se R for menor que o raio de Schwarzschild rs ,
então a solução descreve o que seria um buraco negro. Para determinar o campo gravitacional dentro ou fora do corpo em questão, deve-se descobrir a solução de Schwarzschild
para r = R.
Adotando-se M → 0 ou r → ∞, obtém-se a métrica de Minkowski [12],
ds2 = c2 dt2 − dr2 − r2 dΩ2 .
(2.2)
Em 1917, Willem de Sitter [13] encontrou a ”Solução de Sitter”,
Λr2
gtt − 1 −
3
.
(2.3)
Einstein então, estudou a métrica sob a forma: dS 2 = − cos2 Rr̄ dt2 + dr̄2 +
r̄ Λ
Λ
sen2 Rr̄ dΩ22 para que
com
R
≡
=
sen
, em que r é a coordenada radial
3r
R
3
padrão. Veriﬁcou também que a origem, r̄ = 0, é uma singularidade de coordenadas, e
Λ
que Rr̄ = πR
,
isto
é,
r
=
também é uma singularidade, mas falha na intenção de
2
3
encontrar uma transformação que a elimine. Em 1922, Cornelius Lanczos [14] eliminou a
singularidade de Sitter em
r=
Λ
,
3
(2.4)
escrevendo a métrica como [14]:
ds2 = −dt2 + cosh2 HtdΩ23 .
(2.5)
Em 1924, Sir Arthur Stanley Eddington [15] introduziu as coordenadas de Eddington e reescreveu a métrica de Schwarzschild como [15]:
2m
2
2
(dt − dr)2 .
ds = dsM4 +
r
(2.6)
Em 1925, George Lameı́tre em Cambridge, escreveu a métrica de Sitter [13], como
2t̃
ds2 = −dt̃2 + e R dx2 .
(2.7)
Em 1930, Edmund Stoner [16], considerou que a densidade de estrelas anãs brancas
varia com o quadrado da massa e encontrou uma densidade de uma ordem de magnitude
CAPÍTULO 2. DEFINIÇÃO E HISTÓRICO DOS BURACOS NEGROS
7
maior que a observada anteriormente. Então, Wilhem Anderson [17], postulou que os
elétrons são relativistas e que a densidade é consideravelmente pequena. Em verdade,
Anderson encontrou uma massa crı́tica, quando a densidade tornou-se inﬁnita. Stoner
descreveu então, o que é conhecido agora, como a equação de estado de Anderson-Stoner
para anãs brancas, uma equação relativista de estado para um gás de elétrons degenerado
(zero de temperatura), cuja expressão para o ı́ndice adiabático γ(ρ), varia de 5/3 - limite
não relativista - a 4/3. Stoner conﬁrmou então, a existência de uma massa limitante, ou
seja, 1, 7 vezes a massa solar [7].
No entanto, Chandrasekhar [18] postulou que havia um limite para a repulsão que
o princı́pio da exclusão pode prover. A teoria da relatividade limita a diferença máxima
nas velocidades das partı́culas de matéria da estrela à velocidade da luz. Isto signiﬁca
que, quando a estrela se torna suﬁcientemente densa, a repulsão causada pelo princı́pio
da exclusão será menor que a atração da gravidade - “Limite de Chadrasekhar” [18]
MCh
√ 3
1
ω30 3π c 2
=
,
2
G
(μe mH )2
(2.8)
em que, é a constante de Planck reduzida, c é a velocidade da luz, G é a constante
gravitacional universal, mH é a massa do átomo de hidrogênio, μe é a massa molecular
média do elétron e Ω03 ∼
= 2.018236 é a constante matemática relacionada à equação de
Lane-Emden [20].
Surgiram assim, algumas implicações sobre o destino ﬁnal das estrelas compactas.
Se a massa de uma estrela for menor que o limite de Chandrasekhar ela pode, eventualmente parar de se contrair, e se estabelecer num possı́vel estado ﬁnal, como por exemplo,
uma ”anã branca”, com raio de alguns milhares de quilômetros e densidade de milhares de
toneladas por centı́metro cúbico. Uma anã branca é sustentada pela repulsão do princı́pio
da exclusão entre os elétrons de sua massa, pode-se observar nas ﬁguras 2.1 e 2.2.
Landau [21, 22] percebeu que existia outro possı́vel estado ﬁnal para uma estrela,
também com massa limite de aproximadamente uma ou duas vezes a massa do Sol, porém
muito menor. Essas estrelas seriam sustentadas pela repulsão do princı́pio da exclusão
entre nêutrons e prótons mais do que entre elétrons; seriam, portanto, chamadas “estrelas
de nêutrons” e teriam raio de aproximadamente 16 km, e densidade de bilhões de toneladas
por cm3 . Na época em que isto foi previsto pela primeira vez não havia uma maneira
CAPÍTULO 2. DEFINIÇÃO E HISTÓRICO DOS BURACOS NEGROS
8
Figura 2.1: Diagrama HR teórico mostrando as diversas fases da evolução de uma estrela de 5 massas
solares, a partir da seqüência principal (SP), no extremo esquerdo inferior, e quanto tempo a estrela leva
em cada fase, segundo os cálculos de Icko Iben Jr. (1931-) [19].
possı́vel de observação das estrelas de nêutrons, que só foram detectadas muito mais tarde.
Estrelas com massa acima do limite de Chandrasekhar enfrentam um grande problema quando esgotam seu combustı́vel. Em alguns casos, elas podem explodir; ou então
se orientar de forma a se livrar de matéria suﬁciente a ﬁm de reduzir sua massa até abaixo
do limite e, assim, evitar o colapso gravitacional. Isto contrariava as opiniões de vários
cientistas, inclusive Einstein que, anos antes escrevera um trabalho em que aﬁrmava que
as estrelas não deveriam se contrair até o ponto zero. Chandrasekhar demonstrou que o
princı́pio da exclusão pode não sustar o colapso de uma estrela cuja massa ultrapasse o
limite que estabelecera, o problema da compreensão do que aconteceria com tal estrela, de
acordo com a relatividade geral, foi resolvido pela primeira vez por Robert Oppenheimer
[23], em 1939. Seus resultados, entretanto, sugeriram que não deveria haver consequências empı́ricas passı́veis de serem detectadas pelos telescópios da época, pode-se observar
o destino ﬁnal de estrelas de diferentes massas na ﬁgura 2.2.
O desenvolvimento atual do trabalho de Oppenheimer informa que, o campo gravitacional de uma estrela altera as trajetórias dos raios de luz no espaço-tempo de onde
eles teriam vindo se a estrela não estivesse presente. Os prismas de luz que indicam as
trajetórias seguidas no espaço e no tempo pelos focos de luz emitidos de suas extremi-
CAPÍTULO 2. DEFINIÇÃO E HISTÓRICO DOS BURACOS NEGROS
9
Figura 2.2: Esquema de evolução estelar, não em escala, para massas diferentes. A classiﬁcação espectral
de uma estrela na sequência principal com 0,45 MSol é M1V, 8 MSol é B2V, 10 MSol é B1V e 25 MSol é
O7V [19].
dades são curvados ligeiramente para dentro, perto da superfı́cie da estrela. Isto pode ser
visto nas curvaturas de luz das estrelas distantes observadas durante um eclipse do Sol.
À medida que a estrela se contrai, o campo gravitacional em sua superfı́cie se torna mais
forte e os prismas de luz se curvam mais para dentro. Consequentemente torna-se mais
difı́cil o mecanismo de escape da luz da estrela, fazendo com que ela pareça mais opaca e
avermelhada a um observador que se encontre à distância. Quando a estrela se encolher
até um determinado raio crı́tico, o campo gravitacional de sua superfı́cie se torna tão forte
que os prismas de luz se curvam para dentro, de tal modo que a luz não pode mais escapar.
De acordo com a teoria da relatividade, nada pode se deslocar mais rapidamente do que
a luz. Assim, tem-se um conjunto de eventos e uma região de espaço-tempo, da qual não
é possı́vel escapar para atingir um observador distante. Esta região é chamada de buraco
negro. Seu limite é chamado de horizonte de eventos e coincide com as trajetórias dos
raios de luz que não conseguem escapar do buraco negro [24].
Para entender o que se veria quando uma estrela se desintegrasse para formar um
CAPÍTULO 2. DEFINIÇÃO E HISTÓRICO DOS BURACOS NEGROS
10
buraco negro, é importante lembrar que na teoria da relatividade não existe o tempo
absoluto e que cada observador tem sua própria medida. O tempo para alguém na estrela
será diferente daquele de alguém à distância, devido ao campo gravitacional da estrela.
A gravidade se torna mais fraca quanto mais afastado se estiver da estrela.
Roger Penrose e Stephen Hawking [25], demonstraram que, de acordo com a relatividade geral, deve haver uma singularidade de densidade inﬁnita e curvatura do espaço
tempo dentro de um buraco negro. Isto é quase igual à grande explosão no começo do
tempo; seria apenas um ﬁm do tempo para o corpo em colapso. Nessa singularidade,
as leis cientı́ﬁcas falhariam. Entretanto, qualquer observador que permanecesse fora do
buraco negro não seria afetado por esta falha de previsibilidade, porque nem a luz, nem
qualquer outro sinal poderia atingi-lo a partir da singularidade. As singularidades produzidas pelo colapso gravitacional ocorrem apenas em lugares como os buracos negros,
onde elas podem ser escondidas da visão externa por um horizonte de eventos [7].
O horizonte de eventos, limite da região do espaço-tempo do qual não é possı́vel
escapar, age quase como uma membrana de direção única em volta do buraco negro; em
que objetos podem cair dentro dele, mas nada, jamais, poderá sair de lá pelo mesmo
caminho. O horizonte de eventos é a trajetória, através do espaço-tempo, percorrida pela
luz que está tentando escapar do buraco negro.
Em 1967, o estudo dos buracos negros foi revolucionado por Werner Israel [26].
Israel demonstrou que, de acordo com a relatividade geral, buracos negros estáticos deveriam ser muito simples: perfeitamente esféricos, seu tamanho dependendo apenas de
sua massa. Sugeriu também que quaisquer dois buracos negros com massas equivalentes
seriam idênticos. Poderiam na verdade ser descritos por uma determinada solução das
equações de Einstein conhecida desde 1917, encontrada por Karl Schawrzschild pouco
depois da descoberta da relatividade geral.
Havia, entretanto, uma interpretação diferente do resultado a que Israel [27] chegara,
defendida sobretudo por Roger Penrose e John Wheeler [6]. Penrose e Wheeler argumentavam que os movimentos acelerados atuantes no colapso de uma estrela implicariam
em que as ondas gravitacionais que dela desprendessem a arredondariam cada vez mais
e, portanto, quando se estabelecesse num estado estacionário, ela estaria absolutamente
esférica. Qualquer estrela estacionária, independente da complexidade de sua forma e
estrutura interna, se transformaria depois do colapso gravitacional, num buraco negro
CAPÍTULO 2. DEFINIÇÃO E HISTÓRICO DOS BURACOS NEGROS
11
perfeitamente esférico, cujo tamanho dependeria apenas da massa da estrela em questão.
Cálculos posteriores sustentaram este argumento, que passou, em pouco tempo a ser adotado genericamente.
O resultado de Israel dizia respeito apenas aos buracos negros formados exclusivamente por corpos estacionários. Em 1963, Roy Kerr [28], encontrou um conjunto de
soluções para as equações da relatividade geral que descreviam buracos negros rotativos.
Estes buracos negros giravam a uma razão constante, sua forma e tamanho dependeriam
apenas de sua massa e dessa razão de rotação. Se a rotação for zero, o buraco negro é
perfeitamente redondo e a solução é idêntica à de Schwarzschild. Se a rotação for nãozero, o buraco negro se arqueia extremamente na direção de seu equador e quanto mais
aceleradamente ele girar, mais se arqueará. Assim, para aplicar o resultado de Israel
incluindo os corpos rotativos, foi conjeturado que, qualquer corpo rotativo, que tivesse
sofrido um colapso e formado um buraco negro, poderia eventualmente se estabelecer no
estado estacionário descrito pela solução de Kerr [28, 26, 27].
Em 1970, Brandon Carter [29] demonstrou que, desde que um buraco negro rotativo
estacionário tenha um eixo de simetria, como um ponto de rotação, seu tamanho e forma só
dependerão de sua massa e da razão de rotação. Então, em 1970, Hawking [7] provou que
qualquer buraco negro rotativo estacionário tem, de fato, tal eixo de simetria. Finalmente
em 1973, David Robinson [30] utilizando resultados de Hawking e Carter demonstrou
que a conjetura era correta: um buraco negro deste tipo seria de fato a solução de Kerr.
Assim, depois de um colapso gravitacional, um buraco negro deve se estabelecer num
estado no qual ele pode girar mas não pulsar. Mas ainda, seu tamanho e forma vão
depender apenas de sua massa e da razão de rotação e não da natureza do corpo que teria
entrado em colapso para forma-lo. John Wheeler [6, 7] referindo-se a esse resultado disse
que “Um buraco negro não tem cabelo”. O Teorema da ausência de cabelos é de grande
importância prática porque restringe amplamente os tipos possı́veis de buracos negros.
Pode-se portanto, construir modelos detalhados de objetos que possam conter buracos
negros, e comparar as previsões destes modelos com as observações. Também implica
que uma quantidade de informações sobre o corpo que entrou em colapso deve se perder
quando o buraco negro se forma, porque posteriormente tudo o que será possı́vel medir
do corpo é sua massa e a razão de sua rotação.
Os buracos negros são um dos poucos casos na história da ciência em que a teoria foi
CAPÍTULO 2. DEFINIÇÃO E HISTÓRICO DOS BURACOS NEGROS
12
desenvolvida detalhadamente enquanto modelo matemático antes que houvesse qualquer
evidência observável indicando que estivesse correta. Na verdade, este foi o argumento
principal utilizado pelos contestadores dos buracos negros; não era possı́vel de se acreditar
em objetos cuja única evidência eram cálculos baseados na teoria da relatividade geral.
Em 1963, Marten Schmidt [31], mediu o desvio para o vermelho de um pálido objeto,
semelhante a uma estrela, na direção das fontes de ondas de radio chamada 3C273. Ele
descobriu que era muito grande para ser provocada por um campo gravitacional; se fosse
um desvio gravitacional para o vermelho, o objeto teria que ser tão compacto e estar tão
próximo da Terra que afetaria as órbitas dos planetas do Sistema Solar.
Isso sugeriu que o desvio para o vermelho era, ao contrário, provocado pela expansão do universo, o que, por sua vez, indicaria que o objeto estava muito distante. E, para
ser visı́vel a tamanha distância, o objeto deveria ser muito brilhante; estaria emitindo
uma imensa quantidade de energia. O único mecanismo que se podia pensar ser capaz de
produzir tamanha quantidade de energia parecia ser o colapso gravitacional não de uma
simples estrela, mas de toda a região central de uma galáxia. Inúmeros outros objetos
equivalentes foram descobertos, sempre com um grande desvio para o vermelho.
Mas
todos estavam distantes, apresentando portanto, grande diﬁculdade de observação para
prover evidência conclusiva dos buracos negros.
Em 1967, Jocelyn Bell e seu orientador Antony Hewish [32] observaram objetos
celestes que emitiam ondas de rádio, concluindo-se que estes objetos eram, de fato, estrelas
de nêutrons rotativas, emitindo vibrações de ondas de rádio devido a uma complexa
interação entre seus campos magnéticos e a matéria à sua volta. Tratava-se da primeira
evidência positiva da existência das estrelas de nêutrons. Uma estrela de nêutrons tem
um raio de aproximadamente 16 km, apenas um pouco maior que o raio crı́tico no qual
uma estrela se transforma em buraco negro. Se uma estrela poderia se contrair até este
tamanho tão pequeno, não seria irracional esperar que outras estrelas pudessem fazê-lo
até tamanhos ainda menores e se transformar em buraco negro [7].
O maior desaﬁo em se detectar um buraco negro estaria em conseguir observá-lo
se, por sua própria deﬁnição, ele não emite qualquer luz. Em 1783, John Michell apontou
em seu trabalho pioneiro que um buraco negro exerce força gravitacional sobre os objetos
próximos. Assim, já se tem a evidência da existência de muitos buracos negros na galáxia
e em outras duas vizinhas, chamadas Nuvens de Magalhães. O número de buracos negros
CAPÍTULO 2. DEFINIÇÃO E HISTÓRICO DOS BURACOS NEGROS
13
é provavelmente muito maior do que se imagina; podendo ser muito maior do que o de
estrelas visı́veis, que chegam aproximadamente a cem bilhões, apenas em nossa galáxia,
na ﬁgura 2.3 a ilustração de um buraco negro supermassivo.
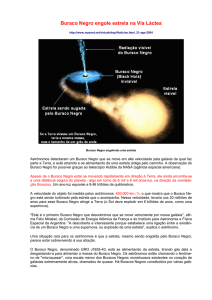
Figura 2.3: Ilustração da Nasa mostra um buraco negro supermassivo no centro da galáxia em espiral
NGC 1365. Este buraco tem 2 milhões de vezes a massa do Sol. [19].
Capı́tulo 3
Estrutura matemática dos buracos
negros
3.1
Introdução
A formação de um buraco negro está relacionada ao ciclo de vida de uma estrela.
Forma-se uma estrela quando uma grande quantidade de gás, geralmente hidrogênio,
começa a colapsar devido à sua atração gravitacional. À medida que se contraem, os
átomos do gás colidem entre si com frequência e velocidade crescentes causando o aquecimento do gás. O gás poderá estar tão quente que, quando os átomos de hidrogênio
colidirem, não irão mais chocar-se uns nos outros mas, se amalgamar formando o hélio.
Esse calor adicional também causa o aumento na pressão do gás, até que seja suﬁciente
para equilibrar a atração gravitacional e pare de se contrair. Assim, as estrelas permanecerão estáveis por muito tempo, com a energia das reações nucleares equilibrando
a atração gravitacional. Eventualmente, a estrela poderá esgotar seu hidrogênio e outros combustı́veis nucleares. Quanto maior a quantidade de combustı́vel que dá origem à
estrela, mais rapidamente ela será consumida. Isso ocorre pois quanto mais compacta a
estrela estiver, mais calor necessitará para equilibrar sua atração gravitacional. E quanto
mais aquecida, mais rapidamente gastará seu combustı́vel [7, 33, 34, 35, 36].
Depois de esgotar todo o seu combustı́vel, uma estrela com mais de duas massas
solares aproximadamente, deverá colapsar em um buraco negro devido às altı́ssimas forças
gravitacionais envolvidas não rivalizadas por nenhuma interação a não ser que ela consiga
ejetar massa suﬁciente para evitar o colapso gravitacional.
CAPÍTULO 3. ESTRUTURA MATEMÁTICA DOS BURACOS NEGROS
3.2
15
Buraco negro de Schwarzschild
O buraco negro mais simples é descrito pela geometria do espaço-tempo de Sch-
warzschild que corresponde ao elemento de linha e que pode ser observada na equação 3.1
abaixo,
ds2 = −x2 dt2 +
em que, x =
1 2
dr + r2 (dθ + sin2 θdφ2 ),
x2
(3.1)
1 − 2M/r é denominado de fator de deslocamento gravitacional para o
vermelho e M é a massa do buraco negro. Trata-se da solução das equações de Einstein
no vácuo Rab = 0, em que Rab é o tensor de Ricci sob condições de estaticidade e simetria
esférica que, ﬁsicamente descreve o estado ﬁnal de uma estrela colapsada anteriormente
sem rotação e sem carga elétrica [36].
As condições mencionadas para se obter tal solução merecem algumas considerações. Inicialmente, este espaço-tempo é estacionário, já que é invariante por translações
temporais, fato que decorre da existência de um campo vetorial de Killing
1
tipo-tempo
ta = (∂t )a , de componentes (1, 0, 0, 0) no sistema particular de coordenadas de Schwarzschild. Em adição a esta caracterı́stica, inclui-se a invariância rotacional daquele elemento
de linha. Pelas coordenadas de Schwarzschild, isso implica na existência de um campo
vetorial de Killing tipo-espaço φa = (∂φ )a , cujo as componentes são (0, 0, 0, 1) [36].
O fato do espaço-tempo de Schwarzschild possuir tais campos vetoriais, permite a
deﬁnição da conservação de energia, vinculada a ta , e de momento angular vinculada a
φa [34]. O elemento de linha acima é singular sobre o raio de Schwarzschild r = 2M , pois
os dois primeiros termos desta métrica assumem os seguintes valores: gtt = 0 e grr = ∞.
Esta singularidade não reﬂete um erro do espaço-tempo em questão, e sim do sistema de
coordenadas de Schwarzschild empregado. Tal fato pode ser entendido imaginando-se que
quando um observador a uma distância ﬁnita do buraco negro, por exemplo em r = r0 ,
move-se geodesicamente e radialmente em sua direção a partir do repouso, pode alcançar
o raio de Schwarzschild (r = 2M) num tempo próprio ﬁnito [37],
4M r0 32 r 32
τ=
,
−
3
2M
2M
(3.2)
que é a quantidade ﬁsicamente relevante [33].
1
Campo vetorial de Killing: nome devido à Wilhelm Killing, é um campo vetorial em uma variedade
riemanniana (ou pseudo riemanniana) que preserva a métrica.
CAPÍTULO 3. ESTRUTURA MATEMÁTICA DOS BURACOS NEGROS
16
O raio de Schwarzschild é essencial para a caracterização do buraco negro. Ele deﬁne uma superfı́cie bidimensional denominada horizonte de eventos - limite de um buraco
negro. O horizonte de eventos, é formado pelas trajetórias, no espaço-tempo, dos raios
de luz que não conseguem se afastar dele, ﬂutuando para sempre em sua margem. As
trajetórias desses raios de luz não podem jamais se aproximar umas das outras [38]. Se o
ﬁzessem, entrariam eventualmente em colisão. Tudo o que passa além dessa fronteira não
pode retornar ao mundo exterior2 [36].
Se os raios de luz que formam o horizonte de eventos, limitação do buraco negro,
jamais se aproximam uns dos outros, sua área pode permanecer a mesma, ou aumentar
com o tempo, mas jamais poderá diminuir, porque isto signiﬁcaria que pelo menos alguns
raios de luz da periferia teriam se aproximado uns dos outros. De fato, a área aumentaria sempre que a matéria ou radiação caı́sse no buraco negro. Se dois buracos negros
colidissem e se fundissem num único, a área do horizonte de eventos, ou do buraco negro
ﬁnal, seria igual ou maior do que a soma das áreas dos horizontes de eventos dos buracos
negros originais [7].
Esta propriedade não decrescente da área do horizonte de eventos apresenta uma
importante restrição no possı́vel comportamento do buraco negro, cujas periferias de
acordo com as duas deﬁnições, seriam as mesmas, e assim também suas áreas, uma vez
que o buraco negro tivesse se estabelecido num estado em que não mudaria ao longo do
tempo. A área do horizonte de eventos que pode ser associdada à área de um buraco
negro, é dada pela equação 3.3 [36],
As =
|gθθ gφφ |dθdφ,
(3.3)
r=2M,t=cte
ou seja,
As = 16πM 2 ,
(3.4)
em que, as variáveis θ e φ são deﬁnidas nos respectivos intervalos: 0 < θ < π e 0 < φ < 2π
[36].
De acordo com a equação (3.1), o espaço-tempo de Schwarzschild possui um caráter
assintoticamente plano, quando a mesma se aproxima da métrica do espaço-tempo de
Minkowski [12] em coordenadas esférico-polares para uma distância radial suﬁcentemente
2
O raio de Schwarzschild de um buraco negro com uma massa igual a da Terra é de apenas 1 cm,
enquanto que um buraco negro de massa igual a do Sol é de 3 Km.
CAPÍTULO 3. ESTRUTURA MATEMÁTICA DOS BURACOS NEGROS
17
grande. A noção de buracos negros depende da existência do conceito de região-assintótica,
sem o qual aﬁrmações do tipo “nada pode escapar” seriam mal deﬁnidas [39].
3.3
Buraco negro de Kerr
O colapso gravitacional de uma estrela com momento angular (relativistica) e
carga elétrica, produz um burago negro diferente daquele tratado até o momento. Este
buraco negro emerge como a solução mais geral das equações de Einstein sob condições de
estacionariedade, simetria axial e ausência de matéria, sendo completamente caracterizado
pela sua massa (energia) M , momento angular J e carga elétrica Q. Somente estes
parâmetros possuem signiﬁcado fı́sico, pois podem ser medidos à distância. Dois buracos
que possuam o mesmo valor para os parâmetros M , J e Q serão considerados iguais
segundo observadores externos. O elemento de linha associado, nas coordenadas de BoyerLindquist, é
2
ds = −
+
em que,
Δ − j 2 sen2 θ
2
dt −
(r2 + j 2 )2 − Δj 2 sen2 θ
2jsen2 θ(r2 + j 2 − Δ)
2
2
sen θdφ +
Δ
dr2 +
dtdφ+
dθ2 ,
(3.5)
= r2 +j 2 cos2 θ, Δ = r2 +j 2 +Q2 −2Mr e j = J/M . A equação (3.5) representa
a geometria do espaço-tempo de Kerr-Newman (KN)3 . No limite em que Q = J = 0, recaı́se na solução de Schwarzschild [36].
Este espaço-tempo também possui a propriedade de ser assintoticamente plano, no
entanto, aparentemente ele possui duas singularidades:
= 0 e Δ = 0. A primeira delas
é a singularidade fı́sica deste espaço-tempo, enquanto que a segunda é ﬁctı́cia e de mesma
natureza daquela representada por r = 2M no espaço-tempo de Schwarzschild. As raı́zes
da equação Δ = 0 são:
3
Buraco negro de Kerr-Newman (KN), refere-se a um buraco negro com massa, momento angular e
carga = 0.
CAPÍTULO 3. ESTRUTURA MATEMÁTICA DOS BURACOS NEGROS
r± =
M 2 − j 2 − Q2 ,
18
(3.6)
sendo que a superfı́cie bidimensional caracterizada por r = r+ e t = cte, deﬁne o horizonte
de eventos do buraco negro de KN. Observa-se que no limite j, Q → 0, tem-se r+ → 2M ,
como esperado.
A área deste horizonte é calculada da seguinte maneira [36], [37]:
2
AKN =
|gθθ gφ φ|dθdφ = 4π (r+
+ j 2) =
r=r+ ,t=cte
= 4π (2M 2 − Q2 + 2M
M 2 − j 2 − Q2 ).
(3.7)
A existência de um horizonte de eventos no espaço-tempo de KN ﬁca condicionada
à satisfação da hipótese adicional M 2 ≥ j 2 +Q2 . Caso contrário, teria-se uma singularidade
“nua”, isto é, não “vestida” por um horizonte de eventos. O fato de singularidades nuas
levarem à impredictabilidade dos eventos de seu futuro causal, levou Penrose a conjecturar
aquilo que ﬁcou conhecido como censura cósmica [40], que em sua versão fı́sica aﬁrma que
o completo colapso gravitacional de um corpo sempre resulta num buraco negro em vez
de uma singularidade nua [34]. O quadrado da norma do campo de Killing ta , ta ta = gu ,
torna-se positivo na região denominada ergosfera, r+ < r < r(θ), em que
r(θ) = M +
M 2 − Q2 − j 2 cos2 θ
(3.8)
deﬁne a superfı́cie de limite estacionário. A denominação ergosfera provém da mudança de
orientação de ta , de tipo-tempo para tipo-espaço, implicando numa não estacionariedade
intrı́nseca de qualquer observador situado nesta região, que é obrigado a rodar na mesma
direção do buraco negro conforme visto por observadores assintóticos
3.4
4
[36].
Espaço Tempo de Minkowski
O espaço-tempo de Minkowski apresenta um diagrama de Carter/Penrose, com
uma forma triangular, conforme ilustrado na ﬁgura 3.1. Correspondem os dois lados da
diagonal ao passado e o futuro nulo inﬁnitos.
4
Este efeito é uma versão extrema do efeito relativı́stico conhecido como arrastamento dos referenciais
inerciais.
CAPÍTULO 3. ESTRUTURA MATEMÁTICA DOS BURACOS NEGROS
19
Estão realmente no inﬁnito, então, todas as distâncias são reduzidas por um fator conforme quando se aproxima do inﬁnito nulo - passado ou futuro. Cada ponto deste triângulo
corresponde a uma 2-esfera de raio r. Na linha vertical à esquerda, r = 0 no que representa o centro de simetria e r → ∞ na direita do diagrama. Pode-se facilmente avistar
a partir do diagrama que cada ponto no espaço-tempo de Minkowski está no passado do
inﬁnito nulo futuro I + , signiﬁcando que não há buraco negro e nem horizonte de eventos
[41].
Figura 3.1: Diagrama Carter-Penrose do espaço tempo de Minkowski de [41].
Entretanto, se existir um corpo esférico em colapso o diagrama irá diferir [25], [41].
Parece o mesmo no passado, mas agora o topo do triângulo foi cortado como pode ser
visualizado na ﬁgura 3.2, e é substituı́do pelo limite horizontal. Esta é a singularidade
que prevê o teorema de Hawking-Penrose 5 .
Em seguida, pode-se veriﬁcar que existem pontos no âmbito desta linha horizontal
5
Teorema (Hawking e Penrose (1970)) [42] Incisos:
I. Rab K a K b ≥ 0 para todo vetor do tipo não-espacial K;
II. M não contém curvas fechadas do tipo temporal Rab K a K b < 0;
III. Cada geodésica do tipo não-espacial, com vetor tangente K, contém um ponto em que
K[a Rb]
[cd] [e
Kf ] K c K d = 0;
IV. Existe pelo menos uma das seguintes opções:
(i) um conjunto compacto atemporal sem bordo;
(ii) uma superfı́cie fechada conﬁnada;
(iii) as geodésicas nulas de algum ponto são eventualmente focadas, ou as geodésicas nulas de alguma
2-superfı́cie fechada são todas convergentes.
CAPÍTULO 3. ESTRUTURA MATEMÁTICA DOS BURACOS NEGROS
20
que não estão no passado do inﬁnito nulo futuro I + , conforme se observa na ﬁgura 3.1.
Expressando-se de outra maneira, existe um buraco negro. O horizonte de eventos é uma
linha diagonal que desce a partir do canto superior direito e intercepta a linha vertical
correspondente ao centro de simetria, como observado na ﬁgura 3.2. Pode ser evidenciado
também na ﬁgura 3.3 [25]. Na ﬁgura 3.4, pode-se observar uma descrição com outra
possı́vel representação do fecho de M̃ [43].
Figura 3.2: Representação de um espaço tempo resultante do completo colapso gravitacional de um
corpo esférico de [25], [33].
Figura 3.3: Um diagrama de acordo com o mesmo espaço-tempo ﬁgura 3.2. Neste caso a região α do
espaço tempo fı́sico está do lado de fora de J − (I+ ) [43].
De acordo com as ilustrações das ﬁguras 3.1, 3.2, 3.3, 3.4, o passado causal do
futuro nulo inﬁnito, J − (I + ), é não singular e não inclui todo o espaço-tempo fı́sico. A
região alfa não está contida em J − (I + ), em contraste com o espaço-tempo de Minkowski
CAPÍTULO 3. ESTRUTURA MATEMÁTICA DOS BURACOS NEGROS
21
J − (I + ), que inclui todo o espaço-tempo fı́sico. A ideia do comportamento adequado de
J − (I + ), não inclui todo o espaço-tempo, remetendo-se à deﬁnição de buracos negros [44].
Figura 3.4: Outra possı́vel representação do fecho de M do espaço tempo fı́sico que fora representado
pictoricamente na ﬁgura anterior. Como na ﬁgura 3.3, as dimensões angulares são suprimidas, desta forma
um ponto determinado deste diagrama representa uma 2-esfera (excetuando-se r = 0 e i0 ) - Diagrama de
Penrose [45].
Deﬁnição: Espaço-tempo fortemente previsı́vel assintoticamente
Seja, (M, gij ), um espaço-tempo assintoticamente plano associado a um espaçotempo não-fı́sico (M̃ , g˜ij ). Diz-se que (M, gij ) é fortemente previsı́vel assintoticamente se,
no espaço-tempo não-fı́sico existe uma região aberta Ṽ ⊂ M̃ com M ∩ J − (I + ) ⊂ Ṽ tal
que, (Ṽ , g˜ij ) é globalmente hiperbólica
6
[41, 40].
Deﬁnição Topológica: Horizonte de eventos do buraco negro
A região do buraco negro B, deste espaço-tempo, deﬁne-se como B = [M −J − (I + )].
Denomina-se a fronteira de B em M , H = J − (I + ) ∩ M como horizonte de eventos [44],
[43]. Assim, de acordo com os trabalhos de Chandrasekhar [44] e Penrose [43], é necessário
que (Ṽ , g˜ij ) seja uma região globalmente hiperbólica de um espaço-tempo não-fı́sico e implica que, (M ∩ Ṽ , gij ) seja uma região globalmente hiperbólica do espaço-tempo fı́sico.
6
Toma-se aqui o fecho de M ∩ Ṽ , gij no espaço-tempo não-fı́sico M̃ , assim, particularmente, i0 Ṽ .
CAPÍTULO 3. ESTRUTURA MATEMÁTICA DOS BURACOS NEGROS
22
Escolhendo-se então, coordenadas normais de Minkowski para N com origem em
p e ε > 0, suﬁcientemente pequeno para que todas as coordenadas normais da bola B
dadas por t2 + x2 + y 2 + z 2 ≤ 2 estejam contidas em Q e uma curva tipo temporal
suﬁcientemente pequena seja também “temporal” com respeito a métrica “planiﬁcada de
Minkowski” 4dt2 − dx2 − dy 2 − dz 2 , sendo u em (− 12 , 0, 0, 0) e v em ( 12 , 0, 0, 0). Então,
qualquer geodésica do tipo temporal γ de um estende-se ao futuro de N até que encontre
o “hemisfério” deﬁnido por t2 + x2 + y 2 + z 2 = ε2 , t > 0.
Deve-se, portanto, cruzar o cone de luz de geodésicas nulas com ponto limite futuro
v, sendo esta a descrição de uma hipersuperfı́cie e que se estende ao passado em B até
que se encontre o hemisfério oposto por t2 + x2 + y 2 + z 2 = ε2 , t ≤ 0. Se q é um ponto
de intersecção de γ com este cone, então, qv é um futuro nulo, assim, não há pontos r no
futuro de q sobre γ, pode-se ter rv no futuro tipo temporal. Supondo-se que aw u, vN .
Então, as geodésicas uw e wv são futuro do tipo temporal. Denotando-se uw, por γ,
pode-se veriﬁcar pelo supra argumento que w não pode estar no futuro de q sobre γ, daı́
w B. Então, u, vN ⊂ B ⊂ Q.
É denominado espaço topológico Hausdorﬀ se quaisquer dois pontos dados possam ser isolados uns dos outros por conjuntos disjuntos. Mais precisamente, um espaço
topológico X é de Hausdorﬀ se houver dois conjuntos abertos U1 , U2 com p1 U1 e p2 U2 ,
com U1 ∩ U2 = [43].
Pode-se ainda, introduzir o seguinte teorema mostrando que a Topologia de Alexandrov é Hausdorﬀ:
3.1 Teorema
As três seguintes restrições em um espaço-tempo M são equivalentes:
(a) M é fortemente causal; [34]
(b) A topologia de Alexandrov concorda com a topologia da variedade;
(c) A topologia de Alexandrov é Hausdorﬀ [43].
Inicialmente observa-se as alı́neas (a) e (b) do T eorema 3.1 : (a) ⇒ (b). Para
mostrar isso, é preciso apenas estabelecer que, em virtude de (a), cada conjunto aberto
na topologia de variedades é aberto na topologia de Alexandrov. Supondo-se que há
CAPÍTULO 3. ESTRUTURA MATEMÁTICA DOS BURACOS NEGROS
23
Figura 3.5: Ilustração: Em (a) : y x curvas do tipo temporal. Em (b), pontos no cojunto aberto de
b também estão em I + + (x) ∩ I − (y), em (c) de acordo com teorema 3.1 [43].
causalidade forte em p e P é um conjunto aberto, na topologia de variedade, contendo
p. Tem-se que mostrar que uma vizinhança de Alexandrov contendo p existe em P . Seja
N uma região simples em P contendo p e seja Q p um conjunto convexo causalmente
aberto, contido em N , que existe por causa da causalidade forte. Da proposição,
3.2 Proposição
Os conjuntos x, y são abertos; dá-se o mesmo com x, yQ se Q for aberto, com
x, y Q [43].
tem-se u, v Q , tal que P u, vN ⊂ Q. Mas, se u, vN = u, v, isso só pode ser devido
à existência de uma viagem de u para v, que deixa e reentra N . Assim, teria também
que sair e reentrar Q, violando a convexidade causal de Q. Assim, p u, vQ ⊂ Q ⊂ P ,
conforme necessário [43].
O fato de que (b) ⇒ (c) é evidente, uma vez que assumindo-se M Haursdorﬀ, resta
mostrar que (c) ⇒ (a) [43].
Assim, supondo-se que, (a) é falsa e a causalidade forte é violada em p. Seja q ≺ p
como no lema abaixo, [40]
3.3 Lema
Seja p M , então, falha a causalidade forte em q, se e somente se, existe q ≺ p,
com q = p, tal que x p e q y juntas impliquem em x y para todo x, y.
CAPÍTULO 3. ESTRUTURA MATEMÁTICA DOS BURACOS NEGROS
24
assim, deve-se mostrar que uma vizinhança de Alexandrov qualquer de p deve intersectar
todas as vizinhanças de Alexandrov de q, de modo que a topologia de Alexandrov deixa de
ser Hausdorﬀ, conforme dito inicialmente. Seja, p u, v e q v, w. Tem-se q ≺ p u,
assim q I − (u). Escolhendo-se y apenas para o futuro de q, dando q y, y I − (u) e
y v, w. Tem-se pelo lema 3.3, x y , assim y x, u também, então x, u ∩v, w =
.
A estrutura topológica do espaço-tempo, é de uso comum em relatividade geral
pois, a teoria da gravidade tem como modelo uma variedade de Lorentz e os conceitos de
topologia, assim, tornam-se importantes na análise local, bem como aspectos globais do
espaço-tempo. O estudo da topologia do espaço-tempo é especialmente importante em
cosmologia.
Os cosmologos e os astrônomos descrevem a geometria do universo que inclui a geometria local e a geometria global. A geometria global descreve o espaço-tempo completo,
contempla a curvatura e a topologia inclusive, ainda que estritamente falando, pertença
a ambos.
No desenvolvimento deste capı́tulo, observou-se que os buracos negros são regiões
no espaço-tempo que delimitam campos gravitacionais tão extremos que nem mesmo
raios de luz podem escapar de seus interiores. No ﬁnal dos anos de 1960, Hawking e
Penrose mostraram que buracos negros, uma vez formados, não podem ser destruı́dos ou
bifurcados, utilizando a topologia para dar o tratamento adequado ao fenômeno, mais
particularmente os Buracos Negros de Schwarzchild e de Kerr.
Capı́tulo 4
Termodinâmica dos Buracos Negros
As relações termodinâmicas apresentadas estarão restritas apenas àquelas que concernem a um buraco negro de Schwarzchild. A razão desta escolha se deve ao fato deste
ser um buraco negro com carga, massa e momento angular nulos.
Neste caso particular, a primeira lei da Termodinâmica dos buracos negros (4.23),
assume inicialmente a seguinte forma
δM = T(bn )δS(bn) ,
(4.1)
em que M é a massa do buraco negro [36].
A temperatura do buraco negro é deﬁnida como sendo
T(bn) =
1
k
=
,
2π
8πM
(4.2)
que, pela restauração das constantes fundamentais, pode-se reescrever como
−8
T(bn) ≈ 6 × 10
M
M
K,
(4.3)
em que, M = 2 × 1033 g representa a massa solar. A temperatura do centro do Sol é
aproximadamente 2 × 107 K, enquanto que, a temperatura superﬁcial é aproximadamente
5, 7 × 103 K. Um buraco negro de massa solar teria, segundo a equação acima, uma
temperatura de aproximadamente 6 × 10−8 K, algo muito pequeno para ser detectável
com as tecnologias atuais [36].
Já a entropia de um buraco negro pode ser dada por
CAPÍTULO 4. TERMODINÂMICA DOS BURACOS NEGROS
S(bn) =
26
As
= 4πM 2 ,
4
(4.4)
em que As = 16πM 2 . Pode-se veriﬁcar dessa forma que, o buraco negro mais entrópico é
o de Schwarzschild.
Reintroduzindo as constantes fundamentais, esta equação pode ser reescrita como,
61
S(bn) =≈ 10
M
M
2
ergK −1 ,
(4.5)
logo, um buraco negro de uma massa solar teria uma entropia associada de 1061 ergK −1 . A
tı́tulo de estimativa, pode-se dizer que a entropia associada ao Sol é da ordem do número
de partı́culas de que ele é composto. Este número é algo como M /mp , em que se designa
de mp a massa do próton (1, 67 × 10−24 g). Então S ≈ 1041 ergK −1
1
[36].
Uma conclusão que pode ser obtida a partir desses resultados é que a origem da
entropia associada aos buracos negros não deve possuir uma natureza térmica. Além
disso, não se conhece qualquer processo dissipativo que possa gerar entropia o bastante,
durante o colapso, de modo a multiplicar a entropia da matéria por um fator 1020 [47]. A
origem dessa discrepância poderá ser melhor entendida quando um tratamento quântico
adequado dos “graus de liberdade do campo gravitacional” for efetuado [34, 36].
Outra grandeza fı́sica associada ao buraco negro de Schwarzchild, que pode ser
obtida deste tratamento, é a capacidade térmica,
C(bn) = T(bn)
∂S(bn)
,
∂T(bn)
= −8πM 2 ,
(4.6)
j=Q=0
conforme as equações (4.2) e (4.3). O fato de a capacidade térmica do buraco negro
de Schwarzschild ser negativa está relacionado ao fato de uma estrela auto-gravitante
arbitrária também possuir uma capacidade térmica negativa, segundo a gravitação newtoniana. Fisicamente, este resultado aﬁrma que a remoção de energia de uma estrela
produz uma contração e posteriormente o aquecimento da mesma. Este é exatamente
o caso para um buraco negro de Schwarzschild, que devido a emissão de partı́culas via
radiação Hawking perde massa, o que proporciona um aquecimento do mesmo, como pode
ser observado pela simples inspeção da equação (4.2) com (∂T (bn)/∂M (bn) < 0) [48].
1
Este é o mesmo resultado obtido por tratarmos o Sol como um corpo negro à temperatura 2 × 107 K
CAPÍTULO 4. TERMODINÂMICA DOS BURACOS NEGROS
27
A manipulação das equações (4.2) e (4.3) permite obter uma relação termodinâmica
entre as quantidades M, S e T do buraco negro, conhecida como relação de Euler 2 ,
1
M = T (bn)S(bn).
2
(4.7)
Este resultado difere daquele da termodinâmica usual pelo fato de a massa do
buraco negro ser uma função homogênea da entropia de grau 1/2. Em outras palavras,
1
sendo S(bn)
→ λS(bn), então M 1 → λ1/2 M , onde λ é um parâmetro de escala.
Para um sistema isolado consistindo de uma caixa de volume V e paredes perfeitamente reﬂetoras contendo uma energia total E na forma de um gás de várias partı́culas
(bósons e férmions, massivos ou não), obtem-se a seguinte relação
4
E = T S,
3
para E = aV T 4 , em que a =
π2
(nb
15
(4.8)
+ 78 nf ) está relacionado à constante de Stefan-
Boltzmann por σ = ac/4, e as variáveis nb e nf representam, respectivamente, o número
de campos massivos e não massivos de bósons e férminos. Portanto, assumindo para este
sistema e o buraco negro as relações do tipo S ∝ T m e E ∝ T n , tem-se
n
E = T S,
m
(4.9)
em que n e m são números inteiros não nulos. Isto é veriﬁcado tanto para um buraco
negro quanto para a radiação de corpo negro ordinária [36].
Por ﬁm, para que o buraco negro seja completamente caracterizado como um sistema termodinâmico, é necessário que, como resultado de uma interação puramente térmica, ele possa trocar energia com um outro sistema de modo que exista a possibilidade
de se encontrar um estado de equilı́brio térmico entre eles.
Esta situação é melhor descrita ao considerar-se um buraco negro imerso num
banho térmico provido pela radiação de corpo negro numa dada temperatura diferente
de zero. A análise completa desta questão aponta para a existência de um estado de
equilı́brio estável entre um buraco negro e a radiação, quando satisfeitas certas condições
especı́ﬁcas [36].
2
Também conhecida como relação de Gibbs-Huhem na forma integral.
CAPÍTULO 4. TERMODINÂMICA DOS BURACOS NEGROS
4.1
28
A mecânica dos buracos negros
Em 1972, Jacob Bekesntein [47] propôs a ideia de que o horizonte de eventos seria
uma medida da entropia de um buraco negro. Porém, se isso fosse verdadeiro, ele deveria
emitir radiação, o que é inadmissı́vel para um buraco negro, uma vez que nada escapa a
ele [49].
No entanto, Stephen Hawking veriﬁcou que de fato haveria a possibilidade de
o horizonte de eventos ser uma medida da entropia de um buraco negro. De acordo
com Hawking, como não existe um vácuo absoluto, haja visto, os limites impostos pelo
“Princı́pio da Incerteza de Heisenberg”, então existem vários pares de partı́culas virtuais
interagindo entre si em torno de um buraco negro, nos quais a energia positiva de uma
partı́cula cancela a energia negativa da outra, e vice-versa. A partı́cula de energia negativa
seria atraı́da pela gravidade fortı́ssima do buraco negro e cairia dentro dele, liberando
sua parceira de energia positiva para o espaço exterior. A energia negativa da partı́cula
dentro do buraco negro diminuiria parte de sua massa, já que cancelaria parte de sua
energia positiva, pois seria aniquilada. A partı́cula de energia positiva liberada não viria
diretamente do buraco negro, como pensado pelo observador externo, mas do espaço
exterior a ele mesmo. Desse modo, a ideia de vácuo quântico resolve esse problema,
admitindo assim que o horizonte de eventos seja uma medida da entropia de um buraco
negro.
4.2
As leis da mecânica dos buracos negros
As quatro leis da mecânica dos buracos negros são propriedades fı́sicas às quais,
acreditam-se, os buracos negros satisfaçam. As leis, análogas às leis da termodinâmica,
foram descobertas por Brandon Carter, Stephen Hawking e James Bardeen [29, 50, ?].
4.2.1
Lei Zero
Deﬁnição:
Se, Tμν obedece à condição de energia dominante, em seguida, a superfı́cie de
gravidade é constante no horizonte de eventos futuros [47, 24, 50].
Seja ξ o vetor normal de Killing a H+ . Então, sendo Rμν ξ μ ξ ν = 0 em H+ , implicam
as equações de Einstein,
CAPÍTULO 4. TERMODINÂMICA DOS BURACOS NEGROS
0 = −Tμν ξ μ ξ ν |H+ ≡ Jμ ξ μ |H−
29
(4.10)
ou seja, J = (−Tνμ ξ ν ) ∂μ é tangente a H+ . Segue-se que J pode ser expandida em uma
base de vetores tangentes a H+ ,
(1)
(2)
J = αξ + b1η + b1η
(4.11)
sobre H+ .
Mas, sendo ξ × ν (i) = 0 do tipo espacial ou nulo (quando b1 = b2 = 0), enquanto
que deve ser do tipo temporal ou nulo pela condição de energia dominante. Assim, a
energia dominante ⇒∝ ξ é então,
0 = ξ[σ Jp ] |H+ = −ξ[λσ Tp ] ξλ |H+
= ξ[λσ Rp ] ξλ |+
H
= ξ[p ∂σ ] k|H+
⇒ ∂σ k ∝ ξσ ⇒ t.∂k = 0 para qualquer vetor t tangente a H+ ⇒ k sobre H+ .
4.2.2
Primeira Lei
Deﬁnição:
Se um buraco negro estacionário de massa M , carga Q e momento angular J, com
horizonte de eventos futuro da superfı́cie de gravidade k, potencial elétrico de superfı́cie
ΦH , e velocidade angular ωH , é perturbado de tal forma que se estabelece outro buraco
negro com massa M + δM , carga Q + δQ e momento angular J + δJ, então [36]
dM =
k
dA + ΩH dJ + ΦH dQ.
8π
(4.12)
Para Q = 0, o Teorema da Unicidade implica que,
M = M (A, J)
(4.13)
A e J possuem dimensões de M 2 (G = c = 1) para a função M (A, J) deve ser homogênea
de grau 12 . Por intermédio do Teorema de Euler de funções homogêneas,
A
∂M
1
∂M
+J
= M
∂A
∂J
2
(4.14)
k
A + ωH J
8π
(4.15)
portanto,
=
CAPÍTULO 4. TERMODINÂMICA DOS BURACOS NEGROS
30
pela fórmula de Smarr.
Então,
A
k
∂M
−
∂A
8π
+J
∂M
− ωH
∂J
= 0,
(4.16)
mas, A e J são parâmetros livres, assim
∂M
k ∂M
=
,
= ωH .
∂A
8π ∂J
4.2.3
(4.17)
Segunda Lei
Deﬁnição:
Se Tμν satisfaz a condição de energia fraca e assumindo a conjectura da censura
cósmica como verdadeira, então a área do horizonte de eventos de um espaço-tempo
assintoticamente plano é uma função não-decrescente do tempo, como demonstrada na
seção que descreve o Teorema da Área, mais adiante.
Bekenstein propôs que um múltiplo ηA /G da área do buraco negro, medido em
unidades do quadrado comprimento de Planck L2p = G/c3 , é atualmente a entropia e
conjectura uma segunda lei generalizada (SLG) que aﬁrma que a soma da entropia fora
do buraco negro e a entropia do buraco negro em si nunca diminuirá [47]:
δ(Sf ora + ηA/G) ≥ 0
(4.18)
Classicamente, parece possı́vel violar a SLG, utilizando processos como por exemplo, uma caixa contendo entropia sob a forma de radiação pode ser atirada para o horizonte de eventos de um buraco negro e cair. Para uma caixa inﬁntesimal ideal, toda
a energia pode ser extraida ao inﬁnito, por isso, quando a caixa é jogada não adiciona
nenhuma massa ao buraco negro. Assim, a área do horizonte de eventos não se altera, mas
a entropia do exterior diminuiu, violando a SLG. Isso pode ser considerada como outra
analogia termodinâmica: a GSL pode ser violada pela adição de entropia de um buraco
negro sem alterar a sua área 3 .
3
Falhas na analogia termodinâmica - Violações da SLG:
i) A temperatura de um buraco negro desvanece.
ii) A entropia é adimensional, enquanto área do horizonte de eventos é um comprimento ao quadrado.
iii) A área de cada buraco negro é separadamente não decrescente, enquanto que apenas a entropia
total é não-decrescente em termodinâmica.
iv) Pode-se adicionar entropia a um buraco negro sem alterar a sua área.
CAPÍTULO 4. TERMODINÂMICA DOS BURACOS NEGROS
4.2.4
31
Terceira Lei
Tem a terceira lei um análogo na fı́sica dos buracos negros, a saber, a superfı́cie de
gravidade do horizonte não pode ser reduzida a zero em um número ﬁnito de passos.
A validade dessa lei é sugerida pelas investigações das órbitas de partı́culas de teste em
torno de um buraco negro rotativo carregado. Uma formulação precisa dessa lei foi dada
e mostrou-se em algumas premissas por Israel [26].
Uma ideia do signiﬁcado da terceira lei pode ser adquirida pensando-se em como
violá-la. Assim,um buraco negro não rotativo k decresce quando adiciona-se massa, então
o buraco negro tem calor especı́ﬁco negativo. Mas, seria necessária uma quantidade inﬁnita
de massa para reduzir k a zero. Um buraco negro rotativo geral com momento angular J
e carga Q tem uma superfı́cie de gravidade e uma área do horizonte de eventos dada por
k = 4πμ/A com A = 4π[2M (M + μ) − Q2 ] e com μ = (M 2 − Q2 − J 2 /M 2 )1/2 .
Tem-se um buraco negro extremo quando μ = 0. Para um buraco negro extremo, k
desvanece e A = 4π(2M 2 −Q2 ) ou seja, um buraco negro extremo tem “temperatura” zero,
mas “entropia” não nula. Se M 2 < Q2 + J 2 /M 2 , em seguida, o espaço-tempo tem uma
singularidade nua e não é um buraco negro em tudo. Assim, se a superfı́cie da gravidade
pode ser reduzida a zero, seria apenas inﬁnintesimalmente longe de criar uma singularidade
nua, violando a Censura Cósmica. Para reduzir a superfı́cie de gravidade a zero, pode-se
tentar injetar uma quantidade suﬁciente de carga ou momento angular para o buraco.
Pode-se supor que se tente jogar uma carga q de massa m em um buraco negro carregado,
não rotativo, de massa M e de carga Q < M , tentando fazer Q + q = M + m, para
que a atração gravitacional seja mais forte que a repulsão eletrostática deve-se escolher
mM > qQ, então q/m < M/Q. Mas, essa desigualdade garante que Q + q < M + m.
Da mesma forma ao se tentar injetar suﬁciente momento angular orbital para um buraco
negro rotativo, deve-se achar que a partı́cula simplesmente perde o buraco. Ao tentar-se
soltar uma partı́cula giratória ao logo do eixo de um buraco negro rotativo da mesma
maneira deve-se imaginar que existe uma força gravitacional spin-spin que é repulsiva e
apenas forte o suﬁciente para impedı́-lo de reduzir k a zero. Ao se tentar soltar uma
partı́cula eletricamente carregada dentro de um buraco negro rotativo ao longo do eixo,
há alguns presumivelmente tipos de “auto-forças” na carga que as repelem do buraco.
O comportamento não decrescente da área de um buraco negro seria muito semelhante ao da entropia.
CAPÍTULO 4. TERMODINÂMICA DOS BURACOS NEGROS
32
Uma aﬁrmação adequada acerca desta ideia é conhecida como a segunda lei da
termodinâmica, que estabelece que a entropia de um sistema isolado sempre aumenta e
que, quando dois sistemas são somados, a entropia do sistema combinado é maior do que
a soma das entropias dos sistemas originais.
A segunda lei da termodinâmica tem um atributo diferente do de outras leis cientı́ﬁcas, pois ela não se aplica a todos os casos, apenas à maioria deles. No entanto, uma
maneira de se violar a segunda lei seria atirando-se qualquer matéria com alguma entropia
no interior do buraco negro. Pode-se naturalmente aﬁrmar que toda a entropia, incluindo
aquela de dentro do buraco negro, não caiu nele - mas, dado que não há jeito de se olhar
para dentro do buraco negro, não se pode ver quanta entropia tem a matéria ali contida
[41].
Dessa forma, a segunda lei da mecânica dos buracos negros está associada ao
teorema da área da Relatividade Geral, obtido no contexto clássico 4 [34] e primeiramente
demonstrado por Hawking [7, 33]. Esta lei aﬁrma que a área de um buraco negro nunca
pode diminuir por nenhum processo fı́sico, ou seja, δA ≥ 0.
Se dois buracos negros se fundissem, a área ﬁnal do horizonte de eventos resultante
será maior ou igual à soma das duas áreas iniciais. Este resultado estabelece uma estreita
analogia entre a área do horizonte de eventos e o conceito de entropia, a menos de fatores
dimensionais. Isso foi primeiramente identiﬁcado e sugerido por Bekenstein [47].
A primeira lei da mecânica dos buracos negros é uma identidade relacionando
as mudanças inﬁnitesimais de massa, M , momento angular J, e área A de um buraco
negro estacionário quando levemente perturbado. A partir da equação (3.7), em que
AKN = (M, J, Q), pode-se obter a função M = M (AKN , J, Q), cujas variações em primeira
ordem dos parâmetros AKN , J e Q resultam em
δM =
∂M
∂A
δA +
J,Q
∂M
∂J
δj +
A,Q
∂M
∂Q
δQ
(4.19)
A,J
omitindo-se a referência KN em A [36].
Os coeﬁcientes associados às variações de J e Q são deﬁnidos da seguinte maneira:
Ω=
4
∂M
∂J
=
A,Q
4πj
,
A
Aquilo que não possui em seu conteúdo elementos próprios da mecânica Quântica.
(4.20)
CAPÍTULO 4. TERMODINÂMICA DOS BURACOS NEGROS
e
Φ=
∂M
∂Q
=
A,J
4πQr+
.
A
33
(4.21)
O estudo do movimento de partı́culas testes carregadas nas proximidades de um
buraco negro de KN atesta que Φ é o potencial elétrico do horizonte do buraco negro,
enquanto Ω é a frequência angular uniforme com a qual partı́culas “caindo” em direção
ao buraco negro são arrastadas pelo horizonte, sendo uma boa deﬁnição da frequência
rotacional do buraco negro. O coeﬁciente associado à variação de A pode ser escrito como
k
=
8π
∂M
∂A
=
J,Q
r+ − M
.
2A
(4.22)
A quantidade k é denominada de gravidade superﬁcial e possui uma interpretação
direta. Para um buraco negro de Schwarzschild, k é o valor limite da força que deve ser
exercida no inﬁnito para manter uma partı́cula de massa unitária sobre o horizonte de
eventos. Nominalmente este valor é 1/4M [36, 51].
As deﬁnições acima permitem reescrever a equação (4.19) como: [50],
δM =
k
δA + ΩδJ + ΦδQ.
8π
(4.23)
O aspecto desta equação é inteiramente similar ao da primeira lei da termodinâmica, a qual aﬁrma que variações inﬁnitesimais na energia, E, entropia, S, e outros
parâmetros de estado extensivos de um sistema, entre estados de equilı́brio térmico contı́guos deste sistema, é dado por
δE = T δS +
X(i) δx(i) ,
(4.24)
i
em que, T é a temperatura do sistema e δx(i) representa a variação do i-ésimo parâmetro
de estado extensivo (excluindo S), enquanto que X(i) ≡ ∂E/∂x(i) é o i-ésimo parâmetro
intensivo (excluindo T ) [36].
Os termos ΩδJ e ΦδQ, que aparecem na equação (4.23), caracterizam o trabalho
feito sobre o buraco negro por um agente externo cuja ação tem por ﬁnalidade aumentar o
momento angular e a carga do buraco negro pelas quantidades δJ e δQ, respectivamente.
Esses elementos de trabalho são bem conhecidos de sistemas mecânicos cujo potencial
elétrico é Φ e a frequência angular é Ω [21, 36].
CAPÍTULO 4. TERMODINÂMICA DOS BURACOS NEGROS
34
A lei zero da mecânica dos buracos negros refere-se a gravidade superﬁcial, que deve
permanecer constante sobre todo o horizonte de eventos de um buraco negro estacionário.
Este resultado é estritamente análogo à zero-ésima lei da termodinâmica, a qual aﬁrma
que a temperatura deve ser uniforme sobre um corpo em equilı́brio térmico [36].
As leis da mecânica dos buracos negros em Relatividade Geral, como enunciadas acima, são notáveis análogos matemáticos das leis da termodinâmica usual, embora diferenciem-se pela natureza de argumentos normalmente utilizados para validá-las.
Contudo, há algumas caracterı́sticas gerais em comum entre elas. Por exemplo, a validade das leis da mecânica dos buracos negros não depende da forma detalhada das
equações de Einstein, assim como a validade das leis da termodinâmica usual não depende do entendimento da dinâmica microscópica do particular sistema. Além disso, os
teoremas de unicidade dos buracos negros estabelecem que um buraco negro estacionário,
isto é, “em equilı́brio”, é caracterizado por um pequeno número de parâmetros (M, J, Q)
assim como os parâmetros de estado da termodinâmica usual [36]. Comparando-se as
zero-ésima, primeira e segunda leis da termodinâmica com as correspondentes leis da
mecânica dos buracos negros encontra-se que as quantidades análogas são, respectivamente: E ↔ M, T ↔ ak, e S ↔ A/8πα, onde α é uma constante indeterminada. Mesmo
no contexto da Relatividade Geral, uma indicação de que essa conexão possa ser envolvida
por um signiﬁcado fı́sico mais profundo surge do fato de que E e M representam a mesma
grandeza fı́sica: a energia total do respectivo sistema [36].
Por outro lado, segundo a mesma Relatividade Geral, a temperatura fı́sica do buraco negro deveria ser nula, sendo notando que classicamente um buraco negro não pode
estar em equilı́brio com a radiação de corpo negro, para qualquer outra temperatura
diferente de zero, pois nenhuma radiação poderia ser emitida a partir dele. Consequentemente, isso também poderia sugerir que a deﬁnição da entropia de um buraco negro a
partir da área do horizonte de eventos seria algo puramente formal [36].
Mas este panorama modiﬁca-se radicalmente ao estudar-se a natureza dos buracos
negros utilizando a Mecânica Quântica [36].
Uma atenção especial é dedicada à terceira lei da termodinâmica, também conhecida como teorema de Planck-Nernst. Esta lei aﬁrma que a entropia tende a zero, S → 0,
quando a temperatura for zero T → 0 para qualquer sistema, em princı́pio [52]. O análogo desta lei falha na mecânica de buracos negros, já que existem buracos negros externos
CAPÍTULO 4. TERMODINÂMICA DOS BURACOS NEGROS
35
M 2 = j 2 + Q2 de área ﬁnita que possuem k = 0. Entretanto, mesmo em termodinâmica
usual, a terceira lei não é considerada uma lei fundamental. Apesar de ser veriﬁcada empiricamente para uma variedade de sistemas, ainda assim é possı́vel encontrar violações a
ela tanto no cenário clássico (gás ideal) quanto no cenário quântico (Sistemas cujo estado
fundamental é altamente degenerado) [21, 36].
4.3
Conjectura da Censura Cósmica
A Conjectura da Censura Cósmica possui aparentemente as singularidades que
estão previstas para o futuro uma propriedade denominada por Penrose [25, 43, 47].
Apresentando-se o que é talvez a mais fundamental questão sem resposta sobre
a teoria do colapso geral-relativista, a saber: existe algum “censor cósmico”, que proı́be
o aparecimento de singularidades nuas, vestidas cada uma em um horizonte de eventos
absoluto? Em certo sentido, um “censor cósmico” pode se mostrar inexistente. Como
observado no teorema de Hawking
5
que a singularidade do “big bang” é, em princı́pio,
observável. Mas não se sabe se singularidades observáveis de fora nunca surgirão em
um colapso genérico que começa a partir de um perfeito estado singular inicial razoável
[41, 53] assim, devem ocorrer consoante a conjectura convenientemente em locais como
por exemplo, os buracos negros, ocultos de observadores externos. Desta forma, qualquer
quebra de previsibilidade que possa ocorrer nestas singularidades não será semelhante ao
que acontece no mundo exterior, pelo menos não de acordo com teoria clássica.
Assim, existe a imprevisibilidade da teoria quântica, que pode ser relacionada ao
poder de possuir no campo gravitacional uma entropia intrı́nseca que não é apenas um
resultado de um grande trabalho de pesquisa.
No entanto, o fato da gravidade possuir uma quantidade que comporta-se inicialmente como a entropia observou-se no acarbouço de uma teoria puramente clássica,
A imagem “clássica” do colapso apresentada pela relatividade geral, é baseada na
solução de Schwarzschild das equações de Einstein no vácuo. Esta solução representa o
campo gravitacional exterior a um corpo esfericamente simétrico [41, 43], a Conjectura da
5
Faz menção o Teorema de Hawking (ou Hawking-Penrose) às seguintes situações sobre a singularidade
nas soluções das equações de campo de Einstein:
(i) A matéria é forçada a ser comprimida para um ponto (uma singularidade tipo espacial).
(ii) Certos raios de luz vêm de uma região com curvatura inﬁnita (singularidade do tipo temporal).
CAPÍTULO 4. TERMODINÂMICA DOS BURACOS NEGROS
36
Censura Cósmica proposta por Penrose não foi provada, porém acredita-se ser verdadeira
para dados iniciais e equações de estado. Possibilita tratar a região em torno de uma
estrela em colapso como assintoticamente plana. Pode-se então, de acordo com o trabalho
de Penrose, mergulhar uma variedade espaço-tempo M conformalmente em uma variedade
com bordo denotada por M [40].
Será o bordo ∂M uma superfı́cie nula e consistirá de dois componentes, futuro
e passado nulos inﬁnitos, denotados respectivamente por I + e I − . Serão dadas duas
condições que caracterizam a Censura Cósmica Fraca:
(i) Supõe-se que geradores de geodésicas nulos de I + são completos em certa métrica
conforme.
(ii) Presume-se que o passado de I + seja globalmente hiperbólico [25, 41].
Isto signiﬁca que não há singularidades nuas que podem ser vistas a partir de
grandes distâncias. Roger Penrose tem uma forma mais forte de censura cósmica que supõe
que o todo o espaço-tempo é globalmente hiperbólico. A hipótese de censura cósmica forte
pode ser expressa, nesta linguagem, aﬁrmando que todo o espaço-tempo é globalmente
hiperbólico, denotando que as singularidades não seriam visı́veis, mesmo para observadores
que se aproximam delas, já na região interior ao horizonte de eventos [40].
4.3.1
Versão Fı́sica da Conjectura da Censura Cósmica
Um colapso gravitacional completo de um corpo resultará sempre em um buraco
negro ao invés de uma singularidade nua, isto é, toda singularidade de um colapso gravitacional é oculta por buracos negros, não podendo ser visualizada por observadores distantes
[43].
4.3.2
Formulação Fı́sica da Conjectura da Censura Cósmica
Todos os espaços-tempos ﬁsicamente módicos são globalmente hiperbólicos, isto
é, à parte de uma possı́vel singularidade inicial, não há sempre singularidades visı́veis
a qualquer observador. Pode-se notar ainda que esta versão da Conjectura da Censura
Cósmica é mais forte do que a anterior (Censura Cósmica Fraca). Nesta, aplica-se a
qualquer observador em qualquer espaço-tempo, não somente para observadores distantes
CAPÍTULO 4. TERMODINÂMICA DOS BURACOS NEGROS
37
em espaços-tempos assintoticamente planos. Na ﬁgura 4.1 pode-se observar que a primeira
versão não implica na segunda [43].
Figura 4.1: Ilustração de uma singularidade nua e uma singularidade oculta por um horizonte de eventos
(adaptada de [41]).
4.4
Topologia dos Buracos Negros
Existe uma analogia entre as leis sob as quais se ediﬁcam a teoria sobre os bu-
racos negros e a termodinâmica. As leis da fı́sica dos buracos negros são oriundas de
rigorosos teoremas da geometria diferencial, enquanto que, as leis da termodinâmica são
aproximações macroscópicas das intrincadas leis da fı́sica microscópica.
A observação que torna mais evidente essa analogia é o teorema que faz menção ao
aumento da área, ocorrendo o mesmo a uma quantidade fı́sica denominada entropia [37],
mais informações sobre este assunto serão observadas no tópico a seguir.
4.5
Teorema da Área
De acordo com Wald [34], se Tμv satisfaz a condição de energia fraca, e assumindo
a conjectura da censura cósmica, descrita na seção anterior, como verdadeira, então a
área do horizonte de eventos de um espaço-tempo assintoticamente plano é uma função
não-decrescente do tempo. Assume a conjectura da censura cósmica que o espaço-tempo
é fortemente assintoticamente previsı́vel, fazendo-se assim necessário requerer a existência
CAPÍTULO 4. TERMODINÂMICA DOS BURACOS NEGROS
38
de uma subvariedade globalmente hiperbólica do espaço-tempo que contenha concomitantemente o espaço-tempo exterior e o horizonte. Consoante aos trabalhos de Geroch
[54, 55, 56], estabelece que nestes casos a existência de uma famı́lia (λ) de hipersuper
fı́cies de Cauchy tal que (λ) ⊂ D+ ( (λ) se, λ > λ [34], como pode ser observada na
ﬁgura 4.2, ilustração adaptada de [25].
Figura 4.2: Ilustração das hipersuperfı́cies de Cauchy.
Pode-se escolher λ como sendo o parâmetro aﬁm em um gerador de geodésica nula
de H+ . Poder-se-á denominar com abuso de linguagem A(λ) área do horizonte, que é
a área da intersecção de (λ) com H+ . A segunda lei da termodinâmica dos buracos
negros aﬁrma que A(λ ) ≥ A(λ) se λ > λ. Ideia de prova para mostrar que A(λ) não
pode diminuir com o aumento λ é suﬁciente para mostrar que cada elemento de área a da
H tem essa propriedade. Considerando que,
da
dλ
= θa, observar-se-á que na segunda lei da
termodinâmica dos buracos negros tem-se θ ≥ 0 em todo H+ . Para supor que isso seja
verdade, deve-se observar que se θ < 0 as geodésicas devem convergir para um foco, ou
seja geodésicas próximas passam por um dado ponto p que intersectam γ a uma distância
ﬁnita aﬁm ao longo dela. O primeiro ponto q para o qual este acontece é denominado
ponto conjugado a p em γ [25].
Na ﬁgura 4.3, pode-se observar pontos em γ além de que não são mais separados.
São do tipo tempo separados por p, o que pode ser exempliﬁcado pelos raios de luz em
um espaço-tempo bidimensional plano e cilindrico, como ilustra a ﬁgura 4.4.
A existência de um ponto conjugado para o futuro de um gerador de geodésica nulo
em H+ signiﬁca que este gerador de H+ tem um ponto limite, entrando em contradição
com os resultados de Penrose e Finkelstein [57], de modo que o ponto conjugado hipotético
não pode existir. Assim, deve ser porque θ ≥ 0 em todo H2 e, portanto, consoante à
CAPÍTULO 4. TERMODINÂMICA DOS BURACOS NEGROS
39
Figura 4.3: Representação esquemática de pontos conjugados, de [25].
Figura 4.4: Ilustração dos pontos conjugados em um espaço-tempo bibimensional de [34].
segunda lei θ = 0 apenas para espaços-tempos estacionários, como pode ser observado na
ﬁgura 4.5.
Assim, A = 0 em
(λ0 ), A = em
(λ1 ) e aumentou para o seu valor ﬁnal
A = 16πM 2 para um buraco negro de Schwarzschild estacionário sobre (λ2 ).
4.5.1
Demonstração do Teorema da Área dos Buracos Negros
Seja, (M, gab ) um espaço fortemente previsı́vel assintoticamente plano satisfazendo
Rab K a k b ≥ 0 para todo k a nulo. Sejam 1 e 2 superfı́cies de Cauchy do tipo espa
cial para a região globalmente hiperbólica Ṽ com 2 ⊂ I + ( 1 ) e seja H1 = H ∩
1,
H2 = H ∩ 2 , aqui H denota o horizonte de eventos H2 ≥ H1 [34].
Prova: Teorema da Área
Estabelecendo-se primeiramente a expansão θ de geradores de geodésicas nulas
de H. Seja
uma superfı́cie de Cauchy do tipo espacial para Ṽ passando por p e
considerando as 2-superfı́cies H = H ∩
. Sendo θ < 0 em p, pode-se deformar para
CAPÍTULO 4. TERMODINÂMICA DOS BURACOS NEGROS
40
Figura 4.5: Ilustração da formação de um buraco Negro de colapso gravitacional esfericamente simétrico
- diagrama de Finkelstein [25], [41], [58].
além em uma vizinhança em p para se observar uma superfı́cie H sobre
com entradas
J − (I + ) e que θ < 0 em toda parte de J − (I + ). Isso leva a uma contradição. Seja
K⊂
uma região fechada entre H e H e seja q I + com q J + (K). Então, o gerador
de geodésica nula de J + (K) é aquele sobre o qual q deve encontrar H ortogonalmente e
então, θ ≥ 0 em todo H.
Um dado p H1 está sobre a geodésica nula futura enextensı́vel γ que está contido
em H. Sendo 2 uma superfı́cie de Cauchy γ deve intersectar 2 no ponto q H2 .
Então, obtem-se um mapa natural em H2 .
Sendo θ ≥ 0, a área da porção de H2 dada pela imagem de H1 sobre este mapa,
deve ser ao menos tão grande quanto a área de H1 . Adicionalmente, sendo o mapa não
necessariamente sobrejetivo, poder-se-ão formar novos buracos negros entre 1 e 2 e a
área de H2 não será menor que H1 , como pode ser visualizado na ﬁgura 4.6.
Nesta secção foram estabelecidas conexões entre a fı́sica dos buracos negros e a
termodinâmica, atentando para eventuais semelhanças e diferenças entre ramos aparentemente bem distintos da fı́sica moderna [34].
Tais propriedades, foram inicialmente veriﬁcadas e estabelecidas na década de 1970,
graças aos trabalhos de S. Hawking e Jacob D. Bekenstein, entre outros, e a profundadas
nos anos seguintes [34].
No desenvolvimento do capı́tulo, inicialmente procurou-se estabelecer a emissão de
radiação com espectro térmico por buracos negros em geral, incluindo os buracos negros
de Schwarzschild. Em seguida, foram correlacionadas as leis termodinâmicas clássicas
CAPÍTULO 4. TERMODINÂMICA DOS BURACOS NEGROS
41
Figura 4.6: Diagrama de Finkelstein ilustrando a colisão de dois buracos negros [58].
com processos envolvendo buracos negros.
Findo o estabelecimento das propriedades gerais, pode-se enﬁm derivar a termodinâmica destes buracos, relacionando-se entropia e área, a ﬁm de se obter expressões para
a temperatura de corpo negro dos mesmos. Com a temperatura, pode-se ainda estudar
as capacidades térmicas, reveladoras de propriedades tı́picas de buracos negros, ou seja,
não compartilhadas por sistemas clássicos [34].
Quanto à descrição da Hipótese da Censura Cósmica, esta oculta a presença do
horizonte de eventos, descreve o que ocorre nas cercanias da singularidade e possui um
importante papel, pois desta forma não há necessidade de se preocupar com o que acontece próximo à singularidade. Nesse contexto, Roger Penrose em 1969 [40], introduziu a
chamada Conjectura da Censura Cósmica, onde aﬁrma que toda singularidade formada
a partir de um colapso gravitacional deve obrigatoriamente apresentar um horizonte de
eventos que a oculte dos observadores externos, não obstante, existem ainda várias evidências favoráveis porém, esta conjectura ainda não foi provada [7].
Tornou-se possı́vel por intermédio da analogia entre a termodinâmica e a dinâmica
dos buracos negros, interpretar conceitos que são caracterı́sticos da fı́sica dos buracos
negros, como seu calor especı́ﬁco negativo e o Teorema da Área. Tendo como ponto de
partida esses estudos pode-se explorar novos modelos de buracos negros e será um prelúdio
para o próximo capı́tulo.
Capı́tulo 5
Aspectos quânticos dos buracos
negros
De acordo com Bekenstein [47], uma imediata consequência dos teoremas de unicidade é a grande quantidade de informação perdida após o total colapso gravitacional.
Assim, como discorrido anteriormente, de acordo com o teorema da ausência de cabelos,
embora um buraco negro seja caracterizado por sua massa, momento angular e carga
elétrica, sua origem provém de algum material composto seguramente por um grande
número de conﬁgurações [6]. Por número de conﬁgurações, fazer-se referência ao número
de microestados de todas as possı́veis estruturas no interior do objeto em questão. Evidentemente, se os efeitos quânticos fossem considerados, esse número de conﬁgurações
para um buraco negro seria inﬁnito, já que ele poderia ter se formado por um número arbitrariamente grande de partı́culas de energia arbitrariamente baixa. Assim, o conteúdo
de informação e, consequentemente de entropia, associado ao buraco negro deveria ser
incrivelmente alto, ou mesmo ilimitado.
Assim, de acordo com Davies, considerando-se a natureza quântica da matéria,
veriﬁca-se que a entropia associada a um buraco negro deve ser ﬁnita [38, 59].
Esta veriﬁcação repousa na relação quântica entre energia e comprimento de onda,
E = h/v, que restringe o tipo de partı́cula contido no buraco negro àquela categoria cuja
energia é tal que seu comprimento de onda esteja compreendido no interior do buraco
negro. Escolhendo o comprimento de onda de uma partı́cula tı́pica como sendo aproximadamente igual ao raio de Schwarzschild, r = 2M , pode-se estimar que sua energia deve ser
da ordem de h/M . Logo, o número máximo de tais partı́culas que estará na composição
CAPÍTULO 5. ASPECTOS QUÂNTICOS DOS BURACOS NEGROS
43
de um buraco negro de massa M é algo em torno de M 2 /h. Uma estimativa rústica para
a entropia nesse caso, conduz a
S̃(bn) = ζ
kM 2
,
h
(5.1)
em que, ζ é um parâmetro adimensional a ser determinado por meio de uma teoria quântica
efetiva da gravitação, e k é a constante de Boltzmann. Esta expressão possui um limite
clássico; a saber S̃(bn) → ∞ quando h → 0 [36].
O resultado obtido em (5.1) demonstra a proporcionalidade entre a entropia associada ao buraco negro e sua área, exatamente como indicado pela segunda lei da mecânica
dos buracos negros. Substituindo o valor da área superﬁcial de um buraco negro de Schwarzschild na equação (5.1), obtem-se,
S̃(bn) =
ζk
16πh
A.
(5.2)
Finalmente, a partir da relação termodinâmica ∂S/∂M = 1/T , deduz-se que a
temperatura de um buraco negro de Schwarzschild seria dada por
T̃(bn) =
h
2ζk
1
,
M
(5.3)
que somente no limite clássico, h → 0, aﬁrma que o buraco negro é completamente
negro (T̃(bn) = 0). Utilizando o valor da gravidade superﬁcial de um buraco negro de
Schwarzchild, k = 1/4M , a equação 5.3 pode ser reescrita como
T̃(bn) =
2h
2ζk
k,
(5.4)
demonstrando a porporcionalidade entre a temperatura associada ao buraco negro e sua
gravidade superﬁcial, segundo a correspondência anteriormente levantada [36].
As equações (5.4) e (5.2) são um vislumbre do que seria a temperatura efetiva
de um buraco negro e sua respectiva entropia, segundo alguma Teoria Quântica da Gravitação. Contudo, o verdadeiro signiﬁcado fı́sico atribuı́do a esses resultados foi dado por
Hawking [53] em 1974, com sua descoberta do efeito térmico de criação de partı́culas ao
redor de um buraco negro [36].
Tal descoberta se apóia na gravitação semi-clássica, também conhecida como Teoria
Quântica de Campos em Espaços-Tempos Curvos, em que os efeitos gravitacionais ainda
CAPÍTULO 5. ASPECTOS QUÂNTICOS DOS BURACOS NEGROS
44
são descritos por um espaço-tempo clássico, mas os demais campos de matéria e radiação,
tais como o escalar e o eletromagnético, são agora tratados como campos quânticos que
se propagam neste espaço-tempo de fundo
1
[36].
Mostrou-se neste contexto que um campo quântico inicialmente em qualquer estado
(não singular), livre de interações como outros campos e consigo mesmo, propagando-se
no espaço-tempo de um buraco negro de Schwarzschild, emitirá partı́culas para o inﬁnito
com um espectro tı́pico de um corpo aproximadamente negro [59] à temperatura
T(bn) =
k
,
2π
(5.5)
denominada temperatura Hawking. Portanto, a temperatura fı́sica do buraco negro é
realmente diferente de zero. Nas palavras de Hawking “classicamente o buraco é negro
mas quânticamente ele é cinza” [7, 41].
Este efeito quântico de criação de partı́culas, radiação Hawking, é aplicável a todos
os campos quânticos livres, permitindo ao buraco negro emitir para o infnito todas as
espécies de partı́culas [34].
O fato de k/2π realmente representar a temperatura fı́sica de um buraco negro,
fornece uma evidência decisiva de que as leis da mecânica dos buracos negros não são
meramente análogos das leis da termodinâmica usual, mas antes, uma manifestação das
leis da termodinâmica ordinária aplicadas a buracos negros. Dessa forma é de se esperar
que
S(bn) =
A
,
4
(5.6)
deva representar a verdadeira entropia fı́sica de um buraco negro. Logo, ζ = 4π em S̃(bn)
e T̃(bn) (e α = 1/2π) [36].
Outro aspecto a ser enfatizado pelo efeito Hawking é que a temperatura dada pela
equação (5.5), é representada como medida por um observador próximo ao inﬁnito. Para
qualquer observador seguindo uma órbita do campo vetorial de Killing tipo-tempo ta no
espaço-tempo de Schwarzschild, a temperatura localmente medida será
T =
1
T(bn )
,
χ
(5.7)
Presumivelmente tal esquema seria somente uma aproximação para um teoria mais profunda (ainda
a ser encontrada), na qual o espaço-tempo também seria quantizado. Entretanto, espera-se que esse
esquema seja uma boa aproximação para muitos propósitos, exceto nas proximidades de singularidades
do espaço-tempo.
CAPÍTULO 5. ASPECTOS QUÂNTICOS DOS BURACOS NEGROS
45
√
em que, χ = −gu. Em outras palavras, a temperatura da radiação Hawking localmente
medida obedece à relação de Tolman [60].
A equação (5.5) mostra que, quando efeitos quânticos são levados em conta, um
buraco negro estará envolto por uma “atmosfera térmica” gerada pela radiação Hawking.
5.1
Radiação de Hawking
Em meados da década de 1970, Stephen Hawking [25] mostrou que um buraco
negro não é tão negro assim graças à mecânica quântica. Num campo de força muito
intenso, como aquele criado pelo campo gravitacional de um buraco negro, é possı́vel a
criação de pares de partı́cula e antipartı́cula. Se um dos elementos do par cair no buraco
negro, o outro será lançado em direção oposta pela conservação do momento. Isto dará
origem a uma radiação de partı́culas que parece emanar do próprio buraco negro. Essa é
a famosa radiação de Hawking. Portanto, o buraco negro pode emitir radiação e não será
completamente invisı́vel graças à esse mecanismo.
Ocorre que a energia também deve ser conservada. Como a partı́cula emitida tem
energia positiva, o seu par, que caiu no buraco negro, tem que ter energia negativa, como
pode ser observado na ﬁgura 5.1. A existência de partı́culas com energia negativa, durante
um intervalo de tempo muito pequeno, é permitido pelas relações de incerteza da mecânica
quântica. Como consequência, além de emitir radiação, a massa do buraco negro também
vai diminuindo. A relatividade restrita não faz distinção entre massa e energia, por isso
absorver uma partı́cula de energia negativa diminuiu a massa do buraco negro. Outra
maneira de compreender a perda de massa é lembrar que ele está emitindo partı́culas.
Esse processo de perda de massa continua até não restar mais nada do buraco negro. Ele
parece ter evaporado-se completamente, emitindo radiação e não deixando nada atrás de
si.
A radiação emitida pelo buraco negro é de um tipo especial chamada radiação
térmica. Tal tipo de radiação transporta apenas informações genéricas sobre o buraco
negro, como sua massa, carga e momento angular. Se, por exemplo, um par de partı́culas
correlacionadas cair no buraco negro, a radiação de Hawking só revelará a massa dessas
partı́culas e a informação sobre sua correlação estará irremediavelmente perdida depois
do processo de evaporação. Isso vale para qualquer coisa que caia no buraco negro. A
CAPÍTULO 5. ASPECTOS QUÂNTICOS DOS BURACOS NEGROS
46
Figura 5.1: Ilustração onde se observa que em (A) o par forma-se e desaparece sem atravessar o
horizonte, em (B) o par forma-se do lado de fora e ambas as partı́culas atravessam o horizonte e em (C)
o par forma-se do lado de fora mas apenas uma das partı́culas atravessa o horizonte.
Informação é perdida à medida que o buraco negro evapora-se e não é possı́vel recuperá-la.
Porém, a mecânica quântica não permite a existência de tais processos onde haja perda
de informação. Isso violaria um dos preceitos básicos da teoria: a evolução unitária. Este
é o paradoxo da informação do buraco negro. É um conﬂito entre a relatividade geral e a
mecânica quântica [61].
A radiação de Hawking, também denominada radiação de Hawking-Bekenstein
é uma radiação térmica com um espectro de corpo negro cuja emissão é prevista para
buracos negros devido a efeitos quânticos. É denominada assim devido ao trabalho de
Stephen Hawking, que forneceu um argumento teórico para a sua existência em 1974, e
o trabalho de Jacob Bekenstein, que previu que buracos negros deveriam ter um número
de temperatura e entropia ﬁnito e não nulo.
O trabalho de Hawking surgiu a partir de sua visita a Moscou em 1973, onde cientistas soviéticos como Iakov, Zel’dovich e Alexander Starobinski [62, 63, 64], mostraram-lhe
que consoante ao princı́pio da incerteza da mecânica quântica, buracos negros rotativos
deveriam criar e emitir partı́culas. O processo de radiação Hawking reduz a massa e a
energia do buraco negro, processo que denomina-se de evaporação do buraco negro, permitindo que eles percam sua massa e energia. Os buracos negros que perdem mais matéria
do que eles ganham por outros meios, tendem a se dissipar, encolher, e ﬁnalmente desaparecer. Prevê-se que os micro buracos negros sejam maiores emissores de radiação do que
os buracos negros mais massivos. Verteu-se a análise de Hawking na primeira percepção
convincente sobre uma possı́vel teoria da gravitação quântica [61].
CAPÍTULO 5. ASPECTOS QUÂNTICOS DOS BURACOS NEGROS
5.1.1
47
Processo de Emissão de Radiação
Associado ao colapso gravitacional de um buraco negro, o espaço-tempo não pode
estar sempre estacionário, razão pela qual espera-se a criação de partı́culas. Se o vácuo
absoluto realmente existisse, ele contrariaria o Princı́pio da Incerteza, de Werner Heisenberg. Isso porque os campos eletromagnéticos e gravitacionais seriam zero, o que equivale
a dizer que a posição e a velocidade de uma partı́cula seriam iguais a zero, ou seja, ambas
estariam determinadas, contrariando o postulado do Princı́pio da Incerteza. O vácuo é
cheio de partı́culas potenciais, pares de matéria e antimatéria virtuais, que estão sendo
constantemente criadas e destruı́das. Elas não existem como entidades observáveis, mas
exercem pressão sobre outras partı́culas, Efeito Casimir [24].
A criação de pares virtuais de partı́culas não viola a lei da conservação da massa/energia
porque elas existem em intervalos de tempo muito pequenos, muito menores do que o
tempo de Planck (10−43s ), de forma que não causam impacto nas leis macroscópicas. O
vácuo quântico é o estado mais baixo de energia, conhecido no universo (ao invés do que
seria o Zero Absoluto). Posto que, o espaço-tempo exterior está estático, pode-se esperar
então que a criação de partı́culas seja um fenômeno transitório determinado pelos detalhes
do colapso [53].
Um possı́vel ﬂuxo de partı́culas, em um dado momento, a frente no tempo é devido
à existência de um horizonte e da independência dos detalhes do colapso. Há um tal ﬂuxo
de partı́culas, e isso acaba por ser térmico - eis a Radiação Hawking.
Considerando-se apenas um campo escalar sem massa em um buraco negro do
espaço-tempo de Schwarzschild denominado Φ. A frequência positiva dos modos de saı́da
de Φ tem o seguinte comportamento
Φω ∼ e−iωu .
(5.8)
Próximo à I + , considere-se uma proximação óptica geométrica em que uma linha
universo da partı́cula é um raio nulo γ, de fase constante u e traçar-se-a este raio para
trás no tempo de I + . Quanto mais a demora em intersectar I + , mais próximo deve
aproximar-se H+ no exterior do espaço-tempo antes de adentrar a estrela.
O parâmetro aﬁm nesta geodésica nula é U , então, U = −. De forma equivalente,
u =
1
log (sobre γ e próximo à H+ ),
k
(5.9)
CAPÍTULO 5. ASPECTOS QUÂNTICOS DOS BURACOS NEGROS
assim,
Φω ∼ exp
iω
log (próximo a H+ ).
k
48
(5.10)
Estas oscilações aumentam cada vez mais rápido à medida que → 0, então a
aproximação óptica geométrica é justiﬁcada por sim. É necessário unir Φω em uma solução
da equação de Klein Gordon próxima de I − . Na aproximação da óptica geométrica, acabase por transportar paralelamente n e l de volta para I − ao longo da continuação de γH.
Seja o encontro desta continuação sobre I − em v = 0, a continuação do raio γ volta para
I − e vai agora encontar I − em uma distância aﬁm ao longo de uma geodésica nula de
saı́da em I − .
O parâmetro aﬁm das geodésicas nulas de saı́da em I − é v (desde ds2 = du dv +
r2 dΩ2 sobre I − ), então v = − em γ assim,
iω
log(−v) ,
Φω ∼ exp
k
(5.11)
isto é, para v < 0. Para v < 0. um raio de saı́da nulo de I − passa por H+ e não alcança
I + , então Φω = Φω (v) em I − , em que
⎧
⎪
⎪
⎪
⎨
Φω (v) =
⎪
⎪
⎪
⎩
exp
iω
k
0
log(−v)
v > 0
v < 0
(5.12)
.
Considerando a Transformada de Fourier,
∞
Φ̃ω =
eiw v Φω (v)dv
−∞
iw
=
log(−v) dv
exp iw v +
k
−∞
0
5.1 Lema:
πω Φ̃ω (−ω ) = − exp −
Φ̃ω (−ω ) para ω > 0
k
(5.13)
5.2 Prova:
Observando a ﬁgura 5.2, escolhe-se uma linha de corte
2
em v plano complexo para estar
ao longo do eixo real.
2
Uma linha de corte é uma curva (com ﬁns possivelmente: aberto, fechado ou semi-aberto) no plano
complexo em que uma função analı́tica com multiplas variáveis é descontı́nua. Por conveniência, linhas
de corte são muitas vezes tomadas como retas ou segmentos de reta [65].
CAPÍTULO 5. ASPECTOS QUÂNTICOS DOS BURACOS NEGROS
49
Figura 5.2: Ilustração representando a Linha de Corte no Plano-v Complexo.
Para ω > 0 gira-se o contorno ao eixo imaginário positivo e deﬁna v = ix para
obter
iω
−iπ/2
log(xe
exp −ω x +
) dx
Φ̃ω (−ω ) = −i
k
0
πω ∞
iω
= − exp
log(x) dx
exp −ω x +
2k
k
0
∞
(5.14)
Sendo ω > 0, a integral converge. Quando ω < 0 contorna-se o eixo imaginário negativo
e deﬁne-se v = −ix para obter
Φ̃ω (−ω ) = i
∞
0
iω
iπ/2
log(xe ) d
exp ω x +
k
πω ∞
iω
= exp −
log(x) dx
exp ω x +
2k
k
0
(5.15)
conclui-se então que,
5.3 Corolário
Um modo da frequência ω positiva sobre I + , ﬁnalmente ﬁcam entre modos mistos positivos
e negativos sobre I − . Pode-se identiﬁcar (para ω positivo)
Aωω = Φ̃ω (ω )
(5.16)
Aωω = Φ̃ω (−ω ) = −e−πω/k Φ̃ω (ω )
(5.17)
CAPÍTULO 5. ASPECTOS QUÂNTICOS DOS BURACOS NEGROS
50
como os coeﬁcientes Bogoliubov 3 , observa-se que,
Bij = −e−πωi/k Aij .
(5.18)
Mas, as equações 5.16 e 5.17 devem satisfazer as relações Bogoliubov, por exemplo,
δij = (AA† − BB † )ij
=
∗
Aik A∗jk − Bik Bjk
k
∗
= eπ(ωi+ωj)/k − 1
Bik Bjk
.
(5.19)
k
Considerando-se i = j para se obter
(BB † )ii =
1
e2πωi/k
−1
,
(5.20)
é necessário o inverso dos coeﬁcientes de Bogoliubov correspondente a um modo positivo
sobre a frequência I − em correspondência positiva, mista e modos de frequência negativos
sobre I + . Como visto anteriormente em B, o inverso do coeﬁciente é
B = −b .
(5.21)
O ﬁnal de partı́culas através de I + dado um vácuo, é
Ni I + = ((B )† (B ))ii = (B ∗ B )ii = (B B )∗ii .
(5.22)
Mas, (B B )ii é também real, assim,
Ni I + =
1
e2πωi/k
−1
.
(5.23)
Esta é a distribuição de Planck para radiação de corpo negro na temperatura de Hawking
TH =
k
.
2π
(5.24)
Conclui-se que, o buraco negro dissipa sua energia a esta temperatura. Da Lei de
Stephan-Boltzmann
4
dE
−σATH4
dt
3
(5.25)
Coeﬁcientes de Bogoliubov: (Transformações de Bogoliubov) Conectam as informações do raio que
vem da região plana do inﬁnito passado e que passa por uma região curva e segue para a região plana do
inﬁnito futuro.
4
A Lei de Stephan-Boltzmann aﬁrma que a energia total irradiada por unidade de área de superfı́cie de
um corpo negro por unidade de tempo j ∗ é diretamente proporcional à quarta potência da temperatura
termodinâmica do corpo negro T : j ∗ = σT 4 .
CAPÍTULO 5. ASPECTOS QUÂNTICOS DOS BURACOS NEGROS
2
π 2 kB
σ=
603 c2
em que A é a área do buraco negro, sendo
E = M c2
2
MG
A =
c2
c3
kB TH ∼
GM
ter-se que,
dM
c4
∼ 2 2
dt
GM
que resulta em um tempo de vida
τ ∼
G2
c4
51
(5.26)
(5.27)
(5.28)
(5.29)
(5.30)
M 3.
(5.31)
Basicamente, o processo de emissão de radiação pode ser entendido imaginandose que a radiação do par partı́cula-antipartı́cula é emitida na superfı́cie do horizonte de
eventos, assim, não provém essa radiação diretamente do buraco negro, mas, é o resultado
de partı́culas virtuais sob o efeito da ação gravitacional do buraco negro [38, 59].
Flutuações quânticas causam um par de partı́cula-antipartı́cula que aparecem próximas ao horizonte de eventos de um buraco negro, enquanto uma das partı́culas do par
cai no buraco negro, a outra escapa, evitando assim sua aniquilação. Objetivando a
preservação do total de energia, a partı́cula que caiu no buraco negro assume uma energia
negativa relativamente a um observador externo do buraco negro. Por intermédio desse
processo, o buraco negro perde massa, bem como, parecerá a um observador externo que
o buraco negro acaba de emitir uma partı́cula [66, 67].
Constitui isso na explicação heurı́stica que melhor corresponde ao cálculo usual.
Um observador externo (no futuro) e distante do buraco negro não pode ver o que há
dentro dele, então possui informações incompletas sobre o estado e observa-se então um
estado com entropia, um estado térmico, supondo-se assim que o buraco negro não é
eterno. Aparentemente a computação original de Stephen Hawking ao lidar com este
caso foi posteriormente diluı́da à sua explicação, assumindo que o buraco negro estaria lá
eternamente, a ﬁm de simpliﬁcar os cálculos.
Assim, fazendo-se uma transformação de Bogoliubov para o vácuo que começa num
estado em que existem pares de partı́culas e antipartı́culas, então este é possivelmente o
elo entre a matemática e a explicação heurı́stica.
Capı́tulo 6
O Fluxo de Ricci
6.1
Introdução
Alguns ﬂuxos geométricos antecederam o ﬂuxo de Ricci, dentre os quais pode-se
destacar o trabalho de Mullins [68], em 1956, cuja proposta era o colapso do ﬂuxo da
curva com o objetivo de modelar o movimento ideal de grãos de fronteira. Pretendendo
representar esse movimento em duas dimensões e, considerando uma regra áurea do movimento de curvas planas, a qual um determinado ponto de uma curva move-se em direção
ao seu centro de curvatura com uma velocidade que é proporcional à curvatura, deduziu
um teorema geral que discorre sobre a mudança de área delimitada por tal curva [69, 70].
Três famı́lias de curvas estão sob os fundamentos da regra citada preservando
transformações de ampliação uniforme, translação e rotação, respectivamente. Partes
destas curvas representam as formas constantes idealizadas de grãos de fronteira sob certas
condições de simetrias.
Destaca-se também o importante trabalho de Eells e Sampson [3] de 1964, ao qual,
Hamilton [1] faz referências em artigos publicados entre 1975 e 1982, em que, introduzem
o mapa harmônico do ﬂuxo de calor, fazendo uso do mesmo para provar a existência de
mapas harmônicos objetivando que as curvaturas seccionais não são positivas.
Em 1974, Firey [71] propôs que o ﬂuxo da curvatura de Gauss modelaria as formas
de pedras gastas e, considerado as situações em que a superfı́cie é invariante e no caso,
menor que a identidade, Gauss escreveu um trabalho sobre um problema fı́sico; a situação das pedras nas praias, cujas ondas batem e promovem desgaste de maneira suave,
de formas regulares, às vezes aparentemente elipsoidais e até mesmo esféricas. Firey en-
CAPÍTULO 6. O FLUXO DE RICCI
53
tão, iniciou seu trabalho com uma idealização do processo de desgaste para materiais
isotrópicos, em seguida, desenvolveu uma equação que rege-o e passou a evidenciar que
uma pedra que é inicialmente convexa e com simetria central tende a assumir uma forma
esférica como consequência da equação que a rege.
Hamilton continuou então, o estudo do mapa harmônico do ﬂuxo de calor considerando variedades com bordo 1 . Em 1978 Brakke [72] estudou os ﬂuxos de curvatura
média e provou propriedades de regularidade que lhes são pertinentes [70].
6.2
O Fluxo de Ricci e outros Fluxos Geométricos
Em Geometria Diferencial deﬁne-se um ﬂuxo geométrico como sendo associado
a um gradiente funcional sobre uma variedade que tem uma interpretação geométrica
geralmente associada a alguma curvatura intrı́nseca ou extrı́nseca, podendo ainda ser
interpretados como ﬂuxos em um espaço de módulos (para os ﬂuxos intrı́nsecos) ou ﬂuxos
em um espaço de parâmetros (para ﬂuxos extrı́nsecos). Pode-se também denominar um
ﬂuxo geométrico por uma equação de evolução geométrica [73, 74, 75].
Deﬁne-se o ﬂuxo de Ricci como sendo um ﬂuxo geométrico intrı́nseco, como por
exemplo, os Fluxos de Calabi e Yamabe, caracterizado por um processo de deformação
da métrica de uma variedade Riemanniana de forma formalmente análoga à difusão de
calor, suavizando irregularidades na métrica.
O ﬂuxo de Ricci foi introduzido pela primeira vez por Richard Hamilton, em 1981,
[1] e é também chamado de ﬂuxo de Ricci-Hamilton. É a principal ferramenta utilizada
para a solução de Grigori Perelman [76, 77, 78], da Conjectura de Poincaré, e também
nas provas dos teoremas da esfera diferenciável por Brendle e Schoen - “Teorema da
Uniformização”.
1
Uma variedade topológica com bordo é um espaço de Hausdorﬀ, no qual cada ponto tem uma
vizinhança homeomorfa a um subconjunto aberto de metade do espaço euclidiano (para um n ﬁxo):
n
|R+
= (x1 , ..., xn ) Rn : Xn ≥ 0. Seja M uma variedade com bordo. O interior de M , denotado MInt , é
o conjunto de pontos em que M que possui vizinhanças homeomorfas a um subconjunto aberto de Rn .
A fronteira de M , denotado ∂M , é o complemento de M em MInt . Os pontos de fronteira podem ser
caracterizados pontos que estão na fronteira do hiperplano (xn = 0) de Rn+ em alguma carta. Se M é
uma variedade com bordo de dimensão n, então MInt é uma variedade (sem bordo) de dimensão n e ∂M
é uma variedade (sem bordo) de dimensão (n − 1).
CAPÍTULO 6. O FLUXO DE RICCI
6.3
54
Teorema de Gage-Hamilton
Seja α0 uma curva suave, simples, fechada e parametrizada ao plano, pode-se
exempliﬁcar a construção de uma deformação de α0 pelo seu vetor de curvatura. A
curva α0 é um mapa que vai de um intervalo [a, b] para R2 sendo que α0 (a) = α0 (b), ou
equivalente a um mapa do cı́rculo unitário S 1 para R2 . Considerando uma famı́lia de
curvas αt em que t ≥ 0 é um parâmetro real denominado tempo, satisfazendo assim, a
evolução da equação [79]
∂α
= Kν,
∂t
(6.1)
em que, K é a curvatura de αt e ν é o vetor normal unitário, como pode ser mostrado na
ﬁgura (6.1).
Figura 6.1: Ilustração de uma curva fechada parametrizada e seus respectivos vetores de curvatura
(curvatura de Gauss) [79].
Nas condições descritas, tem-se que um trivial exemplo seria dado quando α0 é
um cı́rculo. Assim, para cada t > 0, αt também é um cı́rculo com o mesmo centro e
comprimento, sendo assim, uma função estritamente decrescente no tempo. Não é apropriado descrever uma fórmula explı́cita para a solução a partir da qual pode-se veriﬁcar a
existência de um tempo ﬁnito Tmax tal que a solução é deﬁnida apenas para t ∈ [0, Tmax ].
Diz-se que há uma singularidade no tempo Tmax . Como t tende a Tmax , a curva diminui
para um ponto e sua curvatura tende ao inﬁnito em toda parte, como pode ser observado
na ﬁgura (6.2) [74].
Generalizando, quando α0 limita um domı́nio convexo, todos os pontos movemse em direção ao interior deste domı́nio, os de maior curvatura fazem-no mais rápido.
Intuitivamente, isto tende a ser as diferenças de curvatura, tornando a aparência da curva
cada vez mais circular, como se pode observar na ﬁgura (6.3).
CAPÍTULO 6. O FLUXO DE RICCI
55
Figura 6.2: Ilustração que mostra um cı́rculo encolhendo sob o ﬂuxo de redução da curva (todos os
cı́rculos são concêntricos mas, estão dispostos paralelamente para facilitar a visualização de [79]).
Figura 6.3: Ilustração que mostra uma elı́pse encolhendo sob o ﬂuxo de encurtamento da curva e por
ﬁm, se tornando cada vez mais semelhante a um circulo de [79].
Enquanto os pontos de movimento com maior curvatura vão mais rápido, a excentricidade da elipse diminui; próximo da singularidade, a olho nú não será possı́vel distinguila de um cı́rculo.
6.1 Teorema
Seja, [αt ]t∈[0,Tmax ] uma solução máxima do ﬂuxo de encurtamento da curva equação,
então:
i. O comprimento de αt é decrescente em t;
ii. Há uma singularidade, ou seja, Tmax < 1;
iii. Como t tende a Tmax , o diâmetro de ∝t tende a 0 e a relação entre a curvatura máxima
e mı́nima tende a 1.
Apesar do ﬂuxo de Ricci não ser necessariamente uma generalização do ﬂuxo de
redução da curva, já que faz uso de uma noção intrı́nseca de curvatura, o Teorema 6.1,
fornece valiosas referências sobre o tipo de resultados que devem (ou não) ser esperados
sobre o ﬂuxo de Ricci, ou seja, não se deve esperar uma fórmula fechada geral para dados
iniciais ou mesmo uma descrição precisa de uma solução geral, com exceção de informações qualitativas deﬁnidas, monotonicidade de alguma quantidade geométrica, como
fora explicitada na Conclusão (i) do Teorema 6.1.
CAPÍTULO 6. O FLUXO DE RICCI
56
Por outro lado, espera-se provar a existência ou inexistência de uma singularidade,
e obter informações sobre o comportamento da solução próxima do tempo máximo. Essa
construção pode ser generalizada de várias maneiras: pode-se permitir que a curva tenha
singularidades e/ou comprimento inﬁnito, ou substituir o plano por outras superfı́cies.
Existem também várias generalizações importantes e úteis para dimensões maiores,
a mais conhecida é, talvez, o ﬂuxo de curvatura média.
O ﬂuxo de encurtamento da curva é muitas vezes considerado como uma espécie
de equação não linear do calor. De fato, se a curva ∝t é parametrizada por arcos de
comprimento s, então, a equação terá a forma
∂α
∂ 2α
= 2
∂t
∂ s
(6.2)
que é a equação clássica do calor. Esta analogia é um dos princı́pios orientadores do estudo
do ﬂuxo de redução da curva. Uma das principais ferramentas é o princı́pio máximo para
a equação do calor, que diz que o ﬂuxo de calor ﬂui espontaneamente das partes de maior
temperatura para as de menor temperatura, fazendo verter a distribuição de calor de
maneira mais uniforme [2].
Para exempliﬁcar o ﬂuxo de redução da curva, sejam ∝t e βt duas soluções tais
que, para algum tempo t0 , ∝t0 e βt0 em x, observa-se que ∝t move-se mais rápido pelo
fato de não ser apanhado por βt0 , fato pelo qual esta conﬁguração é impossı́vel.
Então, esta discussão acarreta um princı́pio de exclusão que é muito útil, pois
se duas curvas evoluirem pelo ﬂuxo de redução e não possuirem um ponto comum no
tempo 0, então isto continua verdadeiro para todos os tempos t > 0. Pode-se deduzir
a existência de uma singularidade (conclusão (ii) do teorema 6.1) a partir do princı́pio
de exclusão. Para isso, faz-se necessário observar que qualquer curva fechada encontra-se
interna a algum grande cı́rculo. A ideia de usar o princı́pio máximo para obter informações
sobre uma solução geral, comparando-a a uma solução particular, cujo comportamento
é conhecido e também útil para o ﬂuxo de Ricci. No entanto, é necessário que haja no
último caso formas mais soﬁsticadas [2].
CAPÍTULO 6. O FLUXO DE RICCI
6.4
57
Deﬁnição matemática do ﬂuxo de Ricci
Seja M , uma variedade fechada, deﬁne-se um ﬂuxo de Ricci em M , como sendo
um parâmetro da famı́lia gij (t) de métricas Riemannianas sobre M e que satisfaçam a
seguinte equação
∂gij
= −2Rij (T ),
∂t
(6.3)
em que, Rij (T ) é o tensor de Ricci de gij (t).
Com referência à equação (6.3) pode-se imaginá-la como uma espécie de equação
do calor tensorial não-linear. Para simpliﬁcar a notação, escreve-se g para uma métrica
riemanniana e g(t) para uma famı́lia de um parâmetro de métricas, apesar de serem de
fato tensores.
Uma solução para a equação (6.3) (ou um ﬂuxo de Ricci) é uma famı́lia de parâmetros de métricas g(t), parametrizado por t em um intervalo não-degenerado I, sobre
uma variedade suave M satisfazendo a equação (6.3). Considerando-se um ponto inicial
t0 , então, (M, g(t0 )), será denominada métrica inicial para o ﬂuxo de Ricci.
Hamilton evidenciou que o puro problema do valor inicial para a pura Equação
(6.3) sempre tem uma solução única para um tempo suﬁcientemente pequeno, ou seja,
para cada métrica g0 em M , existe um número ε > 0 tal que, há uma única famı́lia de
métricas g(t)t∈[0,ε] , que resolve a equação do ﬂuxo de Ricci e satisfaz g(0) = g0 .
Então, pode-se falar sobre a solução máxima g(t)t∈[0,ε] com dados iniciais, sendo
Tmax ∈ [0, +∞], quando Tmax é ﬁnito, diz-se que o ﬂuxo de Ricci desenvolve uma singularidade. Neste caso, um resultado devido a W. X. Shi [80], implica que a normal do
tensor de Riemann é ilimitada quando T → Tmax . A curvatura blows up 2 no tempo Tmax
contrariamente ao ﬂuxo de de redução da curva no plano, o ﬂuxo de Ricci nem sempre
desenvolverá uma singularidade, por exemplo, se a métrica inicial é Ricci-Flat 3 ou seja, o
tensor de Ricci desvanece, então a solução é constante e, naturalmente, deﬁnida para todos os tempos. O exemplo mais simples de uma singularidade é a esfera em que a métrica
inicial tem curvatura seccional constante e contrai-se para um ponto em um tempo ﬁnito.
Neste caso, a curvatura seccional de g(t) é constante para cada valor de t e tende
2
Blow-up (Expansão): é um tipo de transformação geométrica que substitui um subespaço de um
espaço dado com todas as direções apontando para fora daquele subespaço.
3
Deﬁnem-se Ricci Flat como sendo variedades Riemannianas cuja curvatura de Ricci desvanece, são
casos especiais de variedades de Einstein, em que a constante cosmológica não precisa desvanecer
CAPÍTULO 6. O FLUXO DE RICCI
58
a +∞ quando t tende a Tmax .
6.5
Fluxo de Ricci normalizado
O ﬂuxo de Ricci normalizado é deﬁnido para variedades compactas e pode ser
concedido pela equação 6.4, abaixo,
∂t g = −2Ric(g) +
2
Ravg g,
n
(6.4)
em que Ravg é a média da curvatura escalar, que é obtida a partir do tensor de Ricci,
tomando-se o traço, e n é a dimensão da variedade M . Esta equação normalizada preserva
o volume da métrica.
6.6
Exemplos de soluções exatas do Fluxo de Ricci Variedades de Einstein
Seja g0 uma métrica de Einstein, Ric(g0 ) = λg0 , em que λ é uma constante, então
para qualquer constante positiva c, estabelece-se g = cg0 , tem-se que
Ric(g) = Ric(g0 ) = λg0 =
λ
g.
c
(6.5)
Utilizando a equação (6.5), pode-se construir soluções para a equação do ﬂuxo
de Ricci como segue. Considerando-se g(t) = u(t)g0 , se a famı́lia de métricas de um
parâmetro é uma solução do ﬂuxo de Ricci,
∂g
= u (t)g0
∂t
= −2Ric(u(t)g0 )
= −2Ric(g0 )
= −2λg0 ,
(6.6)
então, u (t) = −2λ e portanto, u(t) = 1 − 2λt. Assim, g(t) = (1 − 2λt)g0 é uma solução
do ﬂuxo de Ricci. Os casos λ > 0, λ = 0 e λ < 0, correspondem respectivamente soluções
CAPÍTULO 6. O FLUXO DE RICCI
59
em que variedade colapsa, mantem-se estável e em expansão. Observa-se no caso em que
a solução colapsa, que a solução existe para t ∈
1
2λ
e se tornará singular em t =
1
.
2λ
Se a variedade M em questão é o espaço euclidiano ou, mais geralmente Ricci-ﬂat,
então, o ﬂuxo de Ricci deixa inalterada a métrica, sendo a recı́proca verdadeira. Por
exemplo, se a esfera tem raio unitário em n dimensões, (S n , g0 ), tem-se
Ric(g0 ) = (n − 1)g0 ,
(6.7)
g(t) = (1 − 2(n − 1)t),
(6.8)
dessa forma, a evolução será
de modo que a variedade colapsará a um ponto em um tempo T =
1
.
2(n−1)
Um outro exemplo seria se, g0 for uma métrica hiperbólica, em tal caso,
Ric(g0 ) = −n(n − 1)g0 ,
(6.9)
g(t) = (1 + 2(n − 1)t)g0 .
(6.10)
a evolução é
Em suma, munindo-se da métrica padrão S n , Rn e H n que são variedades de
Einstein, o ﬂuxo de Ricci colapsará em S n , se manterá constante em Rn e se expandirá
em H n , como foi descrito anteriormente. O ﬂuxo de Ricci em S n tem uma singularidade
em um tempo ﬁnito em que o diâmetro da variedade tende a zero e a curvatura tende
uniformemente a +∞. Um ﬂuxo de Ricci em H n existe para todo t ≥ 0 e como t vai para
o inﬁnito, a distância entre qualquer par de pontos cresce sem limites e a curvatura tende
uniformemente para zero.
Para uma variedade de Einstein compacta, a métrica é inalterada sob o ﬂuxo de
Ricci normalizado, sendo a recı́proca verdadeira.
Seja h0 a métrica sobre S 2 com curvatura Gaussiana constante 12 , deﬁne-se,
h(t) = (1 − t)h0 ,
(6.11)
(S 2 , h(t)), −∞ < t < 1
(6.12)
então, o ﬂuxo,
é um ﬂuxo de Ricci.
CAPÍTULO 6. O FLUXO DE RICCI
60
Tem-se também o produto deste ﬂuxo com o ﬂuxo trivial sobre a reta
(S 2 × R, h(t) × ds2 ),
(6.13)
com −∞ < t < 1, denominado padrão de colapso do cilindro.
6.7
Fluxo de Ricci de forma geométrica
6.7.1
Caso bidimensional
A curvatura de Ricci pode ser descrita em duas dimensões, em termos da curvatura
de Gauss K como Ric(g) = Kg. Trabalhando diretamente a partir da equação (6.3),
observa-se, então, que as regiões em que K < 0 tendem a expandir-se e as regiões onde
K > 0 a colapsar [73].
Por inspeção da ﬁgura (6.4), pode-se então veriﬁcar que o ﬂuxo de Ricci tende a
fazer uma 2-esfera mais esférica. É realmente o caso e há uma excelente teoria que mostra
que em qualquer superfı́cie fechada, o ﬂuxo de Ricci tende a fazer a curvatura de Gauss
constante após a renormalização. Mais demonstrações podem ser observadas no trabalho
de [81].
Figura 6.4: Caso bidimensional da esfera S 2 , com uma ilustração demonstrando que, regiões onde
K < 0, tendem à se expandir e regiões onde K > 0, tendem à colapsar [73].
6.7.2
Caso tridimensional: Neck Pinch
Pode-se perceber uma complexidade maior no caso de variedades tridimensionais
e considerar o ﬂuxo de uma 3-esfera análoga [73].
CAPÍTULO 6. O FLUXO DE RICCI
61
Agora, a esfera de secção transversal é uma S 2 , para o caso supra-descrito, tinha-se
S 1 , observa-se que a ﬁgura (6.5) tem uma curvatura positiva. Sejam e1 , e2 e e3 vetores
ortonormais no ponto p da ﬁgura (6.5), com e3 perpendicular à secção transversal S 2 . Em
seguida, as curvaturas seccionais e Ke2 Λe3 dos “planos” e1 Λe2 e e2 Λe3 são ligeiramente
negativas, como pode ser observado na ﬁgura (6.5). Não obstante, Ke2 Λe2 é extritamente
positiva, portanto,
Ric(e1 , e1 ) = Ke1 Λe2 + Ke1 Λe3 = extritamente positiva.
Ric(e2 , e2 ) = Ke2 Λe1 + Ke2 Λe3 = extritamente positiva.
Ric(e3 , e3 ) = Ke3 Λe1 + Ke3 Λe2 = ligeiramente negativa.
Figura 6.5: Caso tridimensional da esfera S 2 , com uma ilustração demonstrando que, regiões onde
K < 0, tendem à se expandir e regiões onde K > 0, tendem à colapsar [73].
As informações que se apresentam indicam como a variedade sob a ação do ﬂuxo
de Ricci evolui. As distâncias e1 e e2 devem colapsar rapidamente e expandir-se lentamnte
na direção e3 .
Assim, a métrica contrai rapidamente a secção transversal S 2 indicada na ﬁgura
(6.5), enquanto lentamente estica o pescoço, evoluirá para as formas descritas na ﬁgura
(6.6).
Singularidades são tipicamente analisadas por “blowing up”. Quando a curvatura
for grande esta é ampliada, ou seja, reescala ou “blow-up”, de modo que a curvatura já
não é tão grande, como pode ser observado na ﬁgura (6.7).
Neste caso, em particular, o “blow-up” assemelha-se a uma secção do cilindro S 2 ×R
- um pescoço.
CAPÍTULO 6. O FLUXO DE RICCI
62
Figura 6.6: Ilustração de como a métrica evolui contraindo assim a secção transversal S 2 [73].
Figura 6.7: Ilustração da ampliação da curvatura, em que se pode observar o neck pinch se alongando
e limitado por uma esfera S 2 [73].
6.7.3
Neck Pinch degenerado
Um “Blow-up” possı́vel, pode ser feito de forma intuitiva com o neck “pinch dege-
nerado”. Seja o ﬂuxo similar a uma 3-esfera mais assimétrica, como na ﬁgura (6.8).
Figura 6.8: Ilustração apresentando uma 3-esfera assimétrica em que, em L, a região tende a se expandir
e em R, a região tende a colapsar [73].
Se R é uma peça pequena, então o ﬂuxo deve ser visualizado como na ﬁgura (6.9).
Deve-se então, observar a variedade assintoticamente como uma pequena esfera.
Se a peça R é grande, então o ﬂuxo deve se comportar como na ﬁgura (6.10).
Em algum lugar intermediário, quando R é apenas o tamanho certo, tem-se algo
CAPÍTULO 6. O FLUXO DE RICCI
63
Figura 6.9: Representação de uma 3-esfera assimétrica, ilustrando que R colapsou até se tornar um
pequeno ponto que no ﬂuxo do tempo tende a desvanecer [73].
Figura 6.10: Ilustração onde se pode observar a formação de uma singularidade [73].
como observado na ﬁgura (6.11). Se fosse possı́vel ampliar esta singularidade, deveria-se
visualizar algo como na ﬁgura (6.12), o soliton de Bryant [73].
Figura 6.11: Ilustração onde se pode observar a formação de um neck pinch degenerado [73].
Deﬁne-se então, o cilindro colapsado padrão como sendo um modelo para a evolução
de ε − neck. No caso dos ﬂuxos, para se obter os limites geométricos suaves, é necessário
ter o conceito de ε-neck bem consolidado [73]. Nesta forte noção, o pescoço não existe só
numa fatia de tempo, mas existe para trás no ﬂuxo de uma quantidade adequada de tempo
e está próxima ao cilindro, rodada padrão encolhendo em todo o intervalo de tempo. A
existência de gargalos em evolução é explorada quando se estuda limites de ﬂuxos de Ricci
[73].
Para todas as deﬁnições que serão apresentadas a seguir, será ﬁxado 0 < ε < 12 ,
seja k igual ao maior inteiro ou menor igual a ε−1 , em particular para k ≥ 2.
CAPÍTULO 6. O FLUXO DE RICCI
64
Figura 6.12: Ilustração da ampliação do neck pinch degenerado, onde se pode observar um soliton de
Bryant [73].
6.7.4
Deﬁnição de ε-Neck
Seja (N, g) uma variedade riemanniana e x N , um ponto. Então, uma estrutura
ε-neck (N, g) centrado em x, consiste em um difeomorﬁsmo,
ϕ : S 2 × (−−1 , −1 ) → N,
(6.14)
com x ϕ (S 2 × 0), tal que a métrica de R(x) ϕ∗ g está em ε na topologia C [1/2] do
produto da métrica euclidiana usual no intervalo aberto com a métrica de curvatura
gaussiana constante 1/2 sobre S 2 . Também há a seguinte terminologia: N é um ε-neck
centrado em x [2].
A imagem ϕ da famı́lia de subvariedades S 2 × t é denominada de 2-esferas de
ε-neck. Será denominada então de subvariedade ϕ(S 2 × 0) de 2-esferas central de uma
estruta ε-neck. Denota-se por s N : N → R a composição p2 ◦ ϕ−1 , em que p2 é a projeção
de S 2 × (−−1 , −1 ) no segundo fator. O campo vetorial ∂/∂s N , em N é o ϕ∗ do campo
vetorial padrão no intervalo-direção do produto. Utilizando-se também da terminologia
do mais e menos e do ε-neck no sentido claro. A estrutura ε-neck oposta é aquela obtida
−1
por intermédio da composição do pescoço respectivamente como as regiões SN
(0, −1 ) e
−1 −1
SN
( , 0). Para qualquer outra fração, são noções análogas, todas as medidas em relação
a SN : N → (−−1 , −1 ) [2].
Um ε-neck em uma variedade riemanniana X é uma subvariedade N de dimensão
nula e uma ε-estrutura em N centrada em algum ponto X N . A escala de um ε-neck N
centrado em X é R(x)−1/2 . Denota-se a escala de N por rN . Intuitivamente esta é uma
medida do raio da secção transversal S 2 no pescoço. O diâmetro extrı́nseco de qualquer
√
fator S 2 no pescoço está próximo de 2πrN , como pode ser observado na ﬁgura (6.13).
Seja (M, g(t)) um ﬂuxo de Ricci. Um evolving ε-neck centrado em (x, t0 ) e deﬁnido
CAPÍTULO 6. O FLUXO DE RICCI
65
Figura 6.13: Ilustração da secção transversal de uma 2-esfera com curvatura escalar próxima a 1 [2].
para um tempo t1 re-escalado é um ε-neck.
ϕ : S 2 × (−−1 , −1 ) −→∼
= N ⊂ (M, g(t)),
(6.15)
centrado em (x, t0 ) com a propriedade pull back via ϕ da famı́lia de R(x, t0 )g(t )|N , −t1 <
t ≤ 0 em que t1 = R(x, t0 )−1 (t − t0 ). Está ε na topologia C [1/] do produto da métrica
padrão no intervalo que evolui com a métrica em S 2 com curvatura escalar
1
(1−t )
no
tempo t . Um strong ε-neck centrado em (x, t0 ) em um ﬂuxo de Ricci é um evolving εneck centrado em (x, t0 ) e deﬁnido para o tempo re-escalado 1, como pode ser observado
na ﬁgura 6.14.
Figura 6.14: Ilustração onde observa-se a evolução do ε-neck [2].
CAPÍTULO 6. O FLUXO DE RICCI
6.7.5
66
Sóliton
Existe uma noção mais geral e auto-similar do que as soluções que colapsam uni-
formemente ou se expandem. Considera-se estas soluções, “Sólitons de Ricci”, sem a
suposição de que M seja compacta. Para entender tais soluções, deve-se considerar a
ideia de modiﬁcar um ﬂuxo por famı́lia de difeomorﬁsmos.
Um sóliton de Ricci é deﬁnido como sendo um ﬂuxo de Ricci (M, g(t)), 0 ≤ t <
T ≤ ∞, com a propriedade que para cada t [0, T ], existe um difeomorﬁsmo ϕt : M → M
e uma constante σ(t) tal que σ(t)ϕ∗ tg(0) = g(t).
Assim, em um sóliton de Ricci, todas as variedades riemannianas (M, g(t)) são
isométricas além de um fator escala que permite variar com t. O soliton irá colapsar se
σ(t) < 0 para todo t.
Tal ﬂuxo é denominado soliton de Ricci estável, em expansão ou colapsante dependendo se λ = 0, λ < 0 ou λ > 0, respectivamente.
Uma maneira de gerar solitons de Ricci é descrita a seguir. Suponha que se tenha
um campo vetorial X em M , uma constante λ e uma métrica g(0), tal que:
1
−Ric(g(0)) = LX g(0) − λg(0).
2
(6.16)
Seja T = ∞ se λ ≤ 0 e igual a (2λ)−1 se λ > 0. Então, para todo t [0, T ], deﬁne-se a
função
σ(t) = 1 − 2λt,
(6.17)
X(x)
.
σ(t)
(6.18)
e, um campo vetorial
Yt (x) =
Deﬁne-se λt como a famı́lia de um parâmetro de difeomorﬁsmos gerados pelos
campos de vetores Yt dependentes do tempo.
Pode-se aﬁrmar que o ﬂuxo (M, g(t)), em que g(t) = σ(t)λ∗ tg(0), é um soliton e
trata-se de um soliton que colapsa se λ > 0.
Este ﬂuxo satisfaz a equação do ﬂuxo de Ricci, a partir do resultado que segue
∂g(t)
= σ (t)ϕ∗t g(0) + σ(t)ϕ∗t LY (t) g(0) =
∂t
ϕ∗t (−2λ + LX )g(0) = ϕ∗t (−2Ric(g(0))) = −2Ric(ϕ∗t (g(0)))
desde que, Ric(αg) = Ric(g). Para qualquer α > 0, segue que,
(6.19)
(6.20)
CAPÍTULO 6. O FLUXO DE RICCI
67
∂g(t)
= −2Ric(g(t)).
(6.21)
∂t
Será denominado então, um soliton colapsante (M, g(t)), 0 ≤ t < T , de soliton
gradiente colapsante se o campo vetorial X na equação 6.16, é o gradiente de uma função
f suave em M .
6.8
Generalização do ﬂuxo de Ricci
A generalização da equação do ﬂuxo de Ricci não envolve a generalização com a
permuta da equação diferencial parcial (EDP), reciprocamente, mas permite a topologia
global do espaço-tempo diferir de um produto. Há duas maneiras básicas para exibir um
ﬂuxo de Ricci n-dimensional:
(i) como uma famı́lia de um parâmetro de métricas g(t) em uma variedade M, n-dimensional
suave ﬁxa;
(ii) como uma métrica parcial (na direção horizontal) sobre a variedade (n+1)-dimensional
M × I.
Denomina-se uma variedade (n + 1)-dimensional espaço-tempo e as fatias horizontais são as “fatias tipo tempo”.
Por espaço-tempo, entende-se uma variedade (n + 1)-dimensional, M (possivelmente com bordo) equipado com uma função suave t = M → R, que será denominada
tempo e um campo vetorial suave X descrito para os axiomas abaixo:
6.2 Axioma 1
A imagem de t é um intervalo I (possivelmente inﬁnito) e o bordo de M é a préimagem sob t de ∂I.
6.3 Axioma 2
Para cada x M , existe uma vizinhança aberta U ⊂ M de x que é um difeomorﬁsmo f : V × J → U , em que V é um subconjunto aberto em Rn e J é um intervalo com
a supra propriedade do axioma 1, t é a composição de f −1 pela projeção no intervalo J e
do axioma 2, X é a imagem sob f do campo vetorial unitário na direção positiva tangente
à foliação pelas retas v × J de V × J. Observa-se que X (t) = 1.
CAPÍTULO 6. O FLUXO DE RICCI
68
As frações de tempo do espaço-tempo são os conjuntos de nı́vel t, que formam uma
foliação de codimensão 1 de M . Para cada tI tem-se denotado por M t ⊂ M o espaçotempo “t-slice”, ou seja, t−1 (t). Faça-se notar que, cada componente na fronteira de M
está contido em uma única fatia de tempo, sendo que a distribuição horizontal HT M é
a distribuição tangente a esta foliação. A métrica horizontal do espaço-tempo varia como
um produto interior suave positivo deﬁnido em HT M.
É necessário observar que uma métrica horizontal no espaço-tempo induz a métrica
riemanniana ordinária em cada fatia de tempo Mt , assim, e garante-se a reciprocidade.
A curvatura de uma métrica horizontal G com pode ser deﬁnida com uma secção
dual de forma simétrica quadrada, Λ2 HT M, cujo valor em cada ponto x com t(x) = t
é um tensor de curvatura de Riemann usual da métrica induzida em Mt no ponto x,
constituindo-se uma secção suave de Sym2 (Λ2 HT ∗ M ). A curvatura de Ricci e a escalar de
uma métrica horizontal usual são oriundas do universo de suas curvaturas riemannianas.
Deﬁne-se a curvatura de Ricci como uma secção suave de Sym2 (HT ∗ M ), enquanto a
curvatura escalar é uma função suave em M .
Consoante a segunda condição constante na deﬁnição do espaço-tempo, o campo
de vetores X preserva a foliação horizontal e, portanto, a distribuição horizontal.
Deﬁne-se um ﬂuxo de Ricci generalizado n-dimensional como sendo composto por
um espaço-tempo M , (+1)-dimensional e uma métrica horizontal G satisfazendo a equação
de ﬂuxo de Ricci generalizada:
Lx (G) = −2Ric(G)
(6.22)
Seja (M, G) um ﬂuxo de Ricci generalizado e seja xM . Trazendo de volta G para
coordenadas locais V × J deﬁnidas nas proximidades de qualquer ponto de uma famı́lia
de métricas de um parâmetro (V, g(t)), t J, satisfaz-se a equação usual do ﬂuxo de Ricci.
A fórmulas de evolução para as curvaturas de Riemann, de Ricci e a escalar mantêm-se
neste contexto generalizadas.
Naturalmente, o ﬂuxo de Ricci usual constitui-se de um caso particular do ﬂuxo
de Ricci generalizado, em que o espaço-tempo é um produto M × I, com o tempo sendo
a projeção para I e X e o campo vetorial unitário na I-direção positiva.
Consiste em um problema geral em geometria encontrar as melhores destas em uma
dada variedade M n . Naturalmente, o que se realizou anteriormente fora a formalização de
um tal conceito, propondo-se forma de encontrar métricas riemannianas mais adequadas
CAPÍTULO 6. O FLUXO DE RICCI
69
sobre a supra citada variedade, neste contexto, devemos entender a mais adequada como
sendo aquela cuja curvatura escalar seja constante.
Assim, a importância de resultados desta natureza, podem ser observados em ramos
diversos da matemática, uma vez que, a existência de métricas de curvatura constante dão
restrições à topologia da variedade. Isso é útil quando utilizado para o estudo de questões
ligadas à TGR, uma vez que engloba geometria e topologia de variedades.
As teorias relativı́sticas são parte importante das grandes conquistas fı́sicas deste
século. Sua fundamentação matemática está na geometria pseudo-riemanniana, e a base
desta é a Geometria Diferencial.
Capı́tulo 7
R
Visualizações com o Maple 7.1
R
Software Maple R foi desenvolvido nos anos 1980 pelos matemáticos Keith GedO software Maple
des e Gaston Gonnet, na Universidade Waterloo e é considerado uma plataforma de
R é um sistema
computação simbólica genérica com sólida base matemática. O Maple de computação simbólica que facilita a manipulação de expressões matemáticas em forma
R se
simbólica. Entre os sistemas de computação algébrica disponı́veis, o sistema Maple destaca como um dos mais utilizados no mundo inteiro, devido à sua facilidade de uso,
suporte e desenvolvimento contı́nuos, preço acessı́vel e superioridade de algoritmos.
R embora de forma
A computação numérica também pode ser realizada pelo Maple,
R Matlab,
R ou C .
R
mais lenta do que com programas tradicionais, como Fortran,
A
integração numérica/simbólica e a superioridade da sua linguagem de programação, fazem
R possa ser utilizado como uma ferramenta de criação de protótipos de
com que o Maple
R vem sendo desenvolvido em várias partes do mundo,
programas. Há vários anos o Maple
graças ao fato dele ser construı́do sobre sua própria linguagem, não compilada. Somente
um pequeno núcleo básico é compilado.
R é caTal como outros sistemas generalistas de computação algébrica, o Maple
paz de manipular expressões simbólicas e numéricas, incluindo diferenciação, integração,
séries, transformadas de Laplace, equações diferenciais ordinárias e parciais, sistemas de
equações lineares, polinômios, conjuntos, listas, vetores, matrizes e tensores. O Maple
pode gerar resultados numéricos com grande acuracidade utilizando frações exatas e
R pode gerar gráﬁcos em duas ou a três
números com precisão arbitrária. O Maple
R
CAPÍTULO 7. VISUALIZAÇÕES COM O MAPLE 71
dimensões, no contexto deste trabalho, superfı́cies mergulhadas, interativos ou animados.
R como parceiro no desenvolvimento
Por todos estes motivos, elegeu-se o Maple
R encontra-se em sua versão 15, porém neste tradeste trabalho. Atualmente, o Maple
balho, será utilizado o Maple 13. Ao se abrir a tela inicial do software, a interface encontrada pode ser observada na ﬁgura 7.1.
R - versão 13.
Figura 7.1: Ilustração da tela de abertura do Maple
7.2
R para visualização de
Utilização do Maple variedades regulares
7.2.1
Variedades regulares
Variedades regulares são superfı́cies de dimensão m em um espaço euclidiano Rn
com n ≥ m uma direta generalização de objetos que guardam relação de pertinência com
a geometria diferencial clássica, curvas em R2 ou R3 e que possuam vetor e plano tangente
em cada ponto, respectivamente [41].
Dessa forma, retas, arcos de parábola e circunferências são exemplos de variedades de dimensão 1, que podem estar mergulhadas em R3 ou R4 ou espaços de dimensões
maiores, dá-se o mesmo para planos, parabolóides e superfı́cies esféricas, considerando-se
naturalmente, neste caso, como variedades de dimensão 2 que podem estar mergulhadas
R
CAPÍTULO 7. VISUALIZAÇÕES COM O MAPLE 72
em dimensão R3 ou R4 ou mesmo espaços de dimensões maiores, mais informações pertinentes ao assunto e teoremas podem ser encontrados em [41].
Esfera
Inserindo-se na tela do software Maple o comando abaixo,
with(plots);
spacecurve[0, 1 + cos(s), sin(s)], s = 0..P i,
tickmarks = [2, [1, 3, 5], 2],
axes = normal, view = [0..3, 0..3, −1..1];
obtém-se a ﬁgura 7.2, que é uma semicircunferência no plano y, z, com raio 1 e centro (0, 1, 0).
Figura 7.2: Gráﬁco de uma semicircunferência construı́da utilizando-se o software Maple.
Pode-se plotar o gráﬁco também em R3 , digitando-se os comandos abaixo,
plot3d[cos(s) ∗ sin(t), sin(s) ∗ sin(t), cos(t)], s = 0..2 ∗ P i,
t = 0..P i, tickmarks = [2, 2, 2], style = patch, axes = f rame
assim, obtém-se uma esfera, que é uma circunferência - (R1 ), mergulhada no espaço (R3 )
como pode ser observado na ﬁgura 7.3.
R
CAPÍTULO 7. VISUALIZAÇÕES COM O MAPLE Figura 7.3: Gráﬁco uma esfera construı́da utilizando-se o software Maple.
Parabolóide
Inserindo-se na tela do Maple os comandos abaixo,
with(plots);
spacecurve([0, y, y 2 ], y = 0..1, axes = normal),
obtém-se a ﬁgura 7.4, ou seja, uma curva.
Figura 7.4: Curva Espacial construı́da utilizando-se o software Maple.
Neste caso, também pode-se plotar o gráﬁco em R3 , digitando-se os comandos
plot3d[cos(s) ∗ sin(t), sin(s) ∗ sin(t), cos(t)], s = 0..2 ∗ P i, t = 0..P i,
tickmarks = [2, 2, 2], style = patch, axes = f rame
73
R
CAPÍTULO 7. VISUALIZAÇÕES COM O MAPLE 74
assim, obtém-se um cone, que é uma curva - (R1 ), mergulhada no espaço (R3 )como pode
ser observado na ﬁgura 7.5, será um hemisfério sul de uma esfera de raio 1 e centro (0, 0, 0).
Figura 7.5: Gráﬁco de um paraboloide construı́do utilizando-se o software Maple.
Toro
Pode-se observar um último exemplo de formação de variedades utilizando-se o
software Maple, ao se plotar os comandos abaixo,
with(plots);
spacecurve([0, 4 + cos(s), sin(s)], s = 0..2 ∗ P i, tickmarks =
[2, [1, 3, 5], 2], axes = normal, view = [0..5, 0..5, −1..1], scaling = constrained)
obtém-se uma circunferência de raio 1 e centro (0, 4, 0), portanto superfı́cie pertencente
ao R1 , como pode ser observado na ﬁgura 7.6,
Para plotar o gráﬁco em 3D, é preciso digitar os seguintes comandos,
plot3d[(4 + cos(q)) ∗ cos(p), (4 + cos(q)) ∗ sin(p), sin(q)], p = 0..2 ∗ P i,
q = 0..2 ∗ P i, numpoints = 1000, tickmarks = [[−3, 3], [−5, −3, 3, 5], [−1, 1]],
axes = normal, view = [−5..5, −5..5, −2..2], scaling = constrained).
Figura 7.6: Gráﬁco de uma circunferência construı́da utilizando o software Maple.
Assim, obtém-se o T oro, uma superfı́cie mergulhada no espaço R3 , como pode ser observado na ﬁgura 7.7.
Figura 7.7: Gráﬁco de um toro construı́do utilizando-se o software Maple
7.3
Visualizações com o ﬂuxo de Ricci
Simulações numéricas e visualizações com ﬂuxo de Ricci em variedades de dimensão
2 ou 3 decorrem naturalmente devido à natureza geométrica deste.
O ﬂuxo de Ricci atua diretamente sobre a métrica da superfı́cie, tendendo a não
preservar o mergulho. Resultados interessantes podem ser obtidos restringindo as classes
de métricas de revolução, pois as simetrias são preservadas sob o ﬂuxo de Ricci e da
métrica, dependem menor número de parâmetros em tais casos.
Similarmente para variedades tridimensionais como uma 3-esfera, com uma métrica
que é invariante sob a ação de SO(3) 1 , pode a métrica ser representada por uma 2-esfera
1
SO(3): Grupo de todas as rotações sobre a origem do espaço euclidiano R3 no âmbito da operação de
R
CAPÍTULO 7. VISUALIZAÇÕES COM O MAPLE 76
de revolução, sendo que, a distância ao eixo de revolução representa o raio da órbita de
uma 2-esfera. Pode-se também visualizar o desenvolvimento de tais métricas sob o ﬂuxo de
Ricci. Será discorrido sobre como superfı́cies de 3-variedades de revolução permanecerem
mergulhadas em R3 e R4 , respectivamente, sob o ﬂuxo de Ricci e, ﬁnalmente, adentrar
em alguma especulação sobre a ideia do ﬂuxo de Ricci em espaços maiores de métricas
positivas deﬁnidas e indeﬁnidas.
Diferente dos ﬂuxos de curvatura média e aﬁns, que atuam em primeira instância
fazendo com que as superfı́cies tendam a ﬁcar mergulhadas no espaço euclidiano, o ﬂuxo
de Ricci atua diretamente sobre a métrica da superfı́cie, tendendo a não preservá-las
mergulhadas.
É importante portanto, veriﬁcar o fato de que métricas, sob o ﬂuxo de Ricci
preservam o mergulho no espaço euclidiano. Além disso, a chave mestra do fenômeno, o
neck-pinch, que ocorre naturalmente para métricas de revolução. Permite compreender
o comportamento de métricas que tornam-se singulares sob a sua ação. A abordagem
de visualização permite gerar imagens interessantes e informações sobre o neck-pinching.
Evidencia-se que qualquer métrica em uma 2-esfera converge para a métrica esférica sob
o ﬂuxo de Ricci, de modo que o neck-pinching ocorre apenas em dimensões superiores.
Há um número muito limitado de exemplos em que sabe-se completamente como
evolui a métrica. Seria muito útil ter mais exemplos em que o ﬂuxo de Ricci continua por
tempo inﬁnito, sem singularidades em desenvolvimento. Por exemplo, existem trabalhos
importantes, como a cirurgia de Dehn [82, 83, 84], de métricas com curvatura seccional
estritamente negativa em 3-variedades. Assim, mesmo neste caso, não há certeza de
formação de singularidades sob o ﬂuxo de Ricci. Na verdade, não são conhecidos exemplos,
em que uma métrica com todas as curvaturas seccionais negativas ﬂui para uma métrica
com uma curvatura seccional positiva em alguns pontos.
composição. É uma transformação linear que preserva o comprimento de vetores (isto é uma isometria) e
preserva a orientação do espaço. A transformação que preserva o comprimento e que inverte a orientação
é denominada de rotação imprópria. Cada rotação imprópria de um espaço tridimensional euclidiano é
uma rotação seguida de uma reﬂexão em um plano passando pela origem. Compondo dois resultados de
rotações em outra rotação; cada rotação tem uma rotação única inversa, e o mapa identidade satisfaz a
deﬁnição de uma rotação.
Devido às supra descritas, o conjunto de todas as rotações é um grupo sob a composição. Além disso,
o grupo de rotação tem uma estrutura natural de variedade pois as operações de grupo são suaves, por
isso é de fato um grupo de Lie.
R
CAPÍTULO 7. VISUALIZAÇÕES COM O MAPLE 77
Será discutido o motivo pelo qual esferas de revolução de n-dimensão(ões) (k2 = 1),
que são inicialmente isometricamente mergulhadas em um espaço Euclidiano (n + 1)dimensional, permanecem isometricamente mergulhadas, desde que o ﬂuxo de Ricci tenha
uma solução suave.
Posteriormente, pode-se fazer uso de coordenadas extrı́nsecas, úteis para visulização de como os pontos da superfı́cie ou de uma variedade movem-se sob o ﬂuxo de Ricci,
quando visualizados no espaço Euclidiano.
Sobre S n , uma métrica é escolhida da forma ds2 + α2 s dθ2 , em que S é o comprimento do arco ao longo de uma geodésica unindo o Pólo Norte ao Pólo Sul e θ representa
as coordenadas de uma hiperesfera de raio α(s), que é a órbita de uma ação isométrica
de SO(n) em S n , em que o espaço de órbita é um arco, e que s varie entre 0 e L.
Evidencia-se uma condição necessária e suﬁciente para que S n , munida com uma
métrica desta forma, possa ser isometricamente mergulhada em R3 como uma superfı́cie
de revolução, é que a integral da curvatura Gaussiana sobre qualquer ”calota polar” seja
positiva, em tal região e composta de todos os pontos 0 ≤ s ≤ k ou k ≤ s ≤ L, para
algum k com 0 < k < L.
Deve-se observar que uma superfı́cie de revolução em R3 é invariante sob uma ação
isométrica de SO(2) pela rotação sobre o eixo x1 . Da mesma forma que se deﬁne uma
variedade de revolução em R(n+1) como sendo invariante sob a ação isométrica de SO(n)
por rotação sobre o eixo x1 , ﬁnalmente deve-se impor que qualquer variedade de revolução
em R(n+1) tenha no máximo uma componente de intersecção com qualquer hiperplano da
forma x1 = k, para todo k constante.
Da mesma forma, obtem-se a variedade pela rotação do gráﬁco de uma função de
uma variável em torno do eixo x1 , pela ação da SO(n). Deve-se observar que para a
visualização não é essencial, mas é certamente conveniente ter essa restrição.
7.1 Teorema
Suponha que uma métrica da forma ds2 + α2 s dθ2 é escolhida em S n . Então, há
um mergulho isométrico de uma variedade de revolução em R(n+1) , se e somente se a
mesma métrica, vista como S 2 , possa ser isometricamente mergulhada em R3 como uma
superfı́cie de revolução [5].
Para uma calota polar, o Teorema de Gauss-Bonnet evidencia que a soma da
integral da curvatura Gaussiana da calota polar e a integral de curvatura da curva de
R
CAPÍTULO 7. VISUALIZAÇÕES COM O MAPLE 78
fronteira C é π. Portanto, a positividade da primeira integral é equivalente à segunda
integral sendo estritamente menor que π. Nota-se que C é a órbita de SO(2) atuando em
um plano paralelo ao plano x2 x3 e por isso é um cı́rculo padrão neste plano com centro
na intersecção do plano com o eixo x1 . Portanto, a integral de sua curvatura em R3 é
exatamente π e a direção de sua curvatura, cada ponto aponta para o eixo x1 .
Objetivando computar a curvatura da superfı́cie de revolução, tem-se que projetar
sobre o espaço tangente desta superfı́cie, por isso o vetor curvatura projetado será mais
curto, a menos que o plano tangente seja vertical em cada ponto de C. Portanto, a
condição nas calotas polares permanece com o prosseguimento da ação do ﬂuxo de Ricci,
a menos que em algum momento e por algum valor de s, com 0 < s < L, |α (s)| = 1.
portanto, previsa-se mostrar que |α (s)| < 1 continua a ser verdade, longe dos pólos, tanto
tempo como o ﬂuxo de Ricci produz uma solução suave.
7.2 Teorema
Se há um mergulho isométrico de S n como uma variedade de revolução em R(n+1) ,
então a variedade de revolução permanece isometricamente mergulhada, enquanto o ﬂuxo
de Ricci, produz uma solução suave [5].
7.3 Prova
Seja ν = α , em que ν e α são deﬁnidos como funções de s e t tempo, e a derivada
de α é tomada com relação a s. Pela equação 7.3 [85], pode-se veriﬁcar que satisfaz a
seguinte equação de evolução: [5]
∂t ν = νss +
n−2
n−1
ννs +
(1 − ν 2 )ν
α
α2
(7.1)
Inicialmente tem-se |ν| = |αs | < 1, para todos os valores 0 < s < L, por suposição.
Seja t um primeiro valor de tempo em que |ν(st) = 1|, em algum s não correspondente ao
pólo norte ou sul da esfera. Se ν(st) = 1, então é um valor máximo de α reciprocamente se
ν(st) = −1, então este é um valor mı́nimo. Assim, observa-se que consoante ao princı́pio
máximo, que isso resulta em uma contradição, já que 1 − ν 2 = νs = 0 para ambos os
casos. Isso mostra que a esfera mantém-se mergulhada, desde que seja suave.
No trabalho de Rubinstein [5] são apresentadas visualizações do ﬂuxo de Ricci
de superfı́cies e de variedades de revolução 3-dimensionais, isto é um fato muito útil
R
CAPÍTULO 7. VISUALIZAÇÕES COM O MAPLE 79
quando aplicado ao estudo da TRG, que é por excelência uma teoria geométrica. Após o
desenvolvimento dos gráﬁcos, o comportamento dos buracos negros e de outras estruturas
podem assim serem investigados detalhadamente.
O ﬂuxo de Ricci é um adjutório importante, tornando-se fundamental para as
tentativas de provar a Conjectura da geometrização de Thurston [4, 86, 87]. Encontra-se
em Rubinstein [5] a inspiração para resolução de dois problemas, que são o objetivo desta
seção.
R uma
Assim, objetiva-se realizar computacionalmente com o adjutório do Maple forma de realizar superfı́cies mergulhadas para o estudo da evolução e o comportamento
dos buracos negros, isso a partir do tensor métrico, que é um dos componentes necessários
para o desenvolvimento de outro ferramental matemático fundamental, o ﬂuxo de Ricci.
Objetiva-se ainda, obter a visualização das superfı́cies oriundas de métricas a priori para
o estudo dos buracos negros. Não obstante, um prosseguimento exequı́vel e possı́vel
seria prosseguir na direção do trabalho de Rubinstein [5], no que tange ao tratamento da
visualização do ﬂuxo de Ricci. Esta última etapa do processo e as eventuais consequências
e aplicações ao estudo da TRG e do desenvolvimento dos buracos negros será o ponto de
partida para um futuro trabalho.
Capı́tulo 8
Resultados e discussões
Nos próximos tópicos serão apresentados os resultados obtidos utilizando-se o
R aplicado ao estudo da métrica dos buracos negros.
software Maple
R será utilizado para a visualização de superfı́cies mergulhadas,
O software Maple
de forma análoga a descrita por Rubinstein [5], mas neste caso para superfı́cies de revolução, descrita anteriormente, e mesmo uma aplicação do ﬂuxo de Ricci, uma aplicação
ligada ao problema da Esfera Colapsante [81] para modelar o comportamento dos buracos
negros.
8.1
Buraco Negro de Schwarzschild
Nas variedades lorentzianas, os espaços-tempo esfericamente simétricos admitem
uma famı́lia de esferas concêntricas; sendo que pode-se encontrar neste espaço-tempo, uma
carta, a qual denomina-se carta de Schwarzschild, que é um tipo de carta coordenada
polar esférica em um espaço-tempo estático e com simetria esférica. Relativamente às
cartas de Schwarzschild existe uma caracterı́stica notável relacionada à coordenada radial,
possuindo esta uma interpretação geométrica natural, no que tange a área de superfı́cie
e a curvatura gaussiana de cada esfera concêntrica. Dessa forma, as distâncias radiais e
ângulos não possuem uma repreentação mais aperfeiçoada [88, 89, 90].
A métrica é uma forma bilinear simétrica sobre cada espaço tangente de M que
varia de forma diﬁrenciável de um ponto a outro.
80
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
81
Espaço-Tempo de Minkowski
Deﬁnição:
Deﬁne-se um espaço-tempo de Minkowski de quatro dimensões, uma variedade
pseudo-Riemanniana, como sendo um espaço vetorial real, equipado com uma forma
simétrica bilinear não degenerada, com assinatura (−, +, +, +), alternativamente (+, −, −, −).
De forma alternativa é o espaço de Minkowski um espaço pseudo-euclidiano com n = 4 e
n − k = 1, em uma deﬁnição mais ampla permite-se qualquer n > 1. Denominam-se os
elementos do espaço de Minkowski eventos ou quadrivetores. Espaço de Minkowski será
denotado por R1,3 para enfatizar a assinatura ou ainda M 4 [6].
Métrica
Deﬁnição:
Dados dois vetores tangentes u e v em um ponto x em M , a métrica pode ser
avaliada sobre u e v para um dado número real, como sendo [88]:
gx (u, v) = gx (u, v) ∈ R.
(8.1)
Métrica - Forma Local
Deﬁnição:
Em coordenadas locais xμ , μ = 0, ..., 3, pode ser a métrica escrita da seguinte
forma: g = gμν dxμ dxν . Os fatores dxμ são 1-formas gradiente de um campo de coordenadas escalares xμ [90].
Dessa forma, a métrica é uma combinação linear de produtos tensoriais de 1-formas
gradiente de coordenadas. sendo a métrica simétrica tem-se que
gμν = gνμ .
(8.2)
Escrevendo-se o produto tensorial simétrico por justaposição, obtém-se
dxμ dxν = dxν dxμ ,
(8.3)
dessa forma, pode-se escrever a métrica com 10 coeﬁcientes independentes, assim, pode-se
então escrevê-la da seguinte forma
g = gμν dxμ dxν .
(8.4)
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
82
Forma Matricial
Deﬁnição:
A métrica pode ser escrita como uma matriz simétrica 4 × 4 não degenerada, não
singular, com entradas gμν .
8.1.1
Métricas: Codiﬁcação por Vierbein
Deﬁnição: Vierbein
1
Deﬁne-se em μ como sendo a matriz das transformações entre o sistema tétrade e o
sistema de coordenadas
γm = em μ gμ
(8.5)
é uma matriz 4 × 4 com 16 componentes independentes. A inversa de Vierbein em μ é
deﬁnida para a matriz inversa de Vierbein em μ , dessa forma
8.1.2
em μ em ν = δμν
(8.6)
n
em μ e n μ = δ m
(8.7)
Métricas Codiﬁcadas por Vierbein
A distância escalar do espaço tempo é dada por
ds2 = gμν dxμ dxν = gμ gν dxμ dxν = γmn em
μ
en
ν
dxμ dxν
(8.8)
onde resulta que a coordenada métrica gμν seja
gμν = γmn em
μ
en ν .
(8.9)
Seja a métrica de Schwarzschild,
−1
2M
2M
2
2
ds = − 1 −
dt + 1 −
dr2 + r2 dθ2 + r2 sin2 θdφ2 .
r
r
(8.10)
codiﬁcando-a por Vierbein inversa,como pode ser observado na equação 8.11 abaixo,
0
μ
e μ dx =
1
μ
e μ dx =
2M
1−
r
2M
1−
r
12
dt,
−1
2
dr,
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
83
e2 μ dxμ = rdθ,
e3 μ dxμ = rdθ2 μ dxμ = r sin θdφ.
(8.11)
Tendo como ponto de partida a Métrica de Minkowski, descrita em 8.12
dS 2 = c2 dt2 − (dr2 + r2 dθ2 + r2 sin2 θdφ2 )
(8.12)
e, utilizando um procedimento de cálculo descrito em [94], ter-se-á como resultado:
dS 2 = c2 dt2 − dr2 − r2 (dθ2 + sin2 θdφ2 ).
(8.13)
Deve-se reescrever a métrica de forma a apresentar compatibilidade com o problema, ou seja, da seguinte forma
dS 2 = udt2 − V dr2 − wr2 (dθ2 + sin2 θdφ2 ),
(8.14)
sendo u, V e w, funções de r, com w = 1, u = e2v e V = e2λ , considerando v e λ funções
de r, ter-se-a então,
dS 2 = e2v dt2 − e2λ dr2 − r2 dθ2 − r2 sin2 θdφ2 .
(8.15)
As matrizes obtidas com adjutório do Maple, são a representação de um tensor de
segunda ordem, denominado métrica, em particular, é a métrica de Schwarzschild.
Explicitamente, é a inversa vierbein da métrica de Schwarzschild a matriz diagonal
⎛
8.16:
em μ
⎜
⎜
⎜
=⎜
⎜
⎜
⎝
(1 − 2M/r)
0
1
2
⎞
0
(1 − 2M/r)
−1
2
0
0
0
0
0
0
0
r
0
0
0 r sin θ
⎟
⎟
⎟
⎟
⎟
⎟
⎠
e a correspondente Vierbein é 8.17:
⎛
−1
0
0
0
(1 − 2M/r) 2
⎜
⎜
1
⎜
0
(1 − 2M/r) 2 0
0
em μ = ⎜
⎜
⎜
0
0
1/r
0
⎝
0
0
0 1/(r sin θ)
(8.16)
⎞
⎟
⎟
⎟
⎟.
⎟
⎟
⎠
(8.17)
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
8.2
84
Exemplo de Solução e Plotagem dos Gráﬁcos
Segue abaixo a determinação da métrica de Schwarzschild, com o tensor métrico
descrito na forma matricial. Na sequência poderá ser observada também uma breve descrição de propriedades topológicas da solução de Schwarzschild, particularmente no que
tange o Paraboloide de Flamm, que será o gráﬁco plotado. Abaixo, tem-se o código
plotado no Maple.
restart :
with(tensor) :
with(plots) :
with(linalg) :
with(dif f orms) :
coord := [t, r, theta, phi] : #sphericalcoordinates, whichwillbedesignatedintextas[0, 1, 2, 3]
gc ompts := array(symmetric, sparse, 1..4, 1..4) : #metriccomponents
gc ompts[1, 1] := −exp(2 ∗ P hi(r)) : #componentof intervalattached tod(t)2
gc ompts[2, 2] := exp(2 ∗ Lambda(r)) : #componentof intervalattachedtod(r)2
gc ompts[3, 3] := r2 : #componentof intervalattachedtod(theta)2
gc ompts[4, 4] := r2 ∗ sin(theta)2 : #componentof intervalattachedtod(phi)2
g := create([−1, −1], eval(gc ompts)) : #covariantmetrictensor
ginv := invert(g, detg ) : #contravariantmetrictensor
Considerando-se a matriz 8.17, cujo cálculo é realizado pelo software Maple, tem-se
que, a partir da descrição do formalismo da tétrada e das descrições das substituições das
variáveis W = 1, u = eφ(r) e V = e2λ .
A matriz 8.18 é obtida a partir da plotagem comando abaixo no software Maple
ginv := invert(g, detg ) : #contravariantmetrictensor
assim, obtém-se a componente contravariante 8.18, uma vez que a matriz 8.17 é composta por componentes contravariantes.
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
⎛⎡
⎡
⎢
⎜⎢
⎜⎢
⎢
⎜⎢
⎢
⎢compts = ⎢
table ⎜
⎜⎢
⎢
⎜⎢
⎢
⎝⎣
⎣
−e
85
⎤⎞
⎤
2φ(r)
0
0
e
2Λ(r)
0
0
0
0
0
0
r2
0
0
0
0
r2 sin(θ)2
⎥⎟
⎥
⎥⎟
⎥
⎥⎟
⎥
⎥ , indexchar = [−1, −1]⎥⎟ . (8.18)
⎥⎟
⎥
⎥⎟
⎥
⎦⎠
⎦
Na matriz 8.19, tem-se a descrição dos componentes da matriz que é obtida a partir
da plotagem do comando abaixo no softtware Maple,
⎛⎡
⎡
⎜⎢
⎢
⎜⎢
⎢
⎜⎢
⎢
⎢
⎢
table ⎜
⎜⎢compts = ⎢
⎜⎢
⎢
⎝⎣
⎣
⎤⎞
⎤
−1
0
0
0
0
1
e2Λ(r)
0
0
0
0
1
r2
0
0
0
0
1
r 2 sin(θ)2
e2φ(r)
⎥⎟
⎥
⎥⎟
⎥
⎥⎟
⎥
⎥ , indexchar = [1, 1]⎥⎟ .
⎥⎟
⎥
⎥⎟
⎥
⎦⎠
⎦
(8.19)
Na matriz 8.20 tem-se os componentes da matriz que fornecerão condições para
deﬁnir a métrica, seguindo-se para a matriz 8.21, onde ocorrerá o mesmo que em 8.19.
gm atrix := getc ompts(g).
gm atrix := getc ompts(g)
⎡
⎢
⎢
⎢
table ⎢
⎢
⎢
⎣
−e
⎤
2φ(r)
0
0
e
2Λ(r)
0
0
0
0
0
0
r2
0
0
0
0
r2 sin(θ)2
⎥
⎥
⎥
,⎥
⎥.
⎥
⎦
(8.20)
coord := [t, r, theta, phi];
schc ompts := array(symmetric, sparse, 1..4, 1..4);
schc ompts[1, 1] := expand(subs(P hi(r) = −(1/2)∗ln(r)+(1/2)∗ln(r−2∗M ), gm atrix[1, 1]));
schc ompts[2, 2] := expand(subs(Lambda(r) = −(1/2) ∗ ln(1 − 2 ∗ M/r), gm atrix[2, 2]));
schc ompts[3, 3] := gm atrix[3, 3];
schc ompts[4, 4] := gm atrix[4, 4]; sch := create([−1, −1], eval(schc ompts))
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
⎛⎡
⎡
⎜⎢
⎢
⎢
⎜⎢
⎜⎢
⎢
⎢compts = ⎢
table ⎜
⎜⎢
⎢
⎜⎢
⎢
⎣
⎝⎣
−1 +
86
⎤
2M
r
0
0
0
0
1
1− 2M
r
0
0
0
0
r2
0
0
0
0
r2 sin θ2
⎤⎞
⎥
⎥⎟
⎥
⎥⎟
⎥
⎥⎟
⎥ , indexchar = [−1, −1]⎥⎟ . (8.21)
⎥
⎥⎟
⎥
⎥⎟
⎦
⎦⎠
getc ompts(sch)
⎡
⎢
⎢
⎢
table ⎢
⎢
⎢
⎣
8.2.1
−1 +
⎤
2M
r
0
0
0
0
1
1− 2M
r
0
0
0
0
r2
0
0
0
0
r2 sin θ2
⎥
⎥
⎥
⎥.
⎥
⎥
⎦
(8.22)
Parabolóide de Flamm
O paraboloide de Flamm, também denominado diagrama mergulhado, é utilizado
para a visualização da curvatura espacial da métrica de Schwarzschild, e é uma superfı́cie
de curvatura gaussiana negativa [91]. O Parabolóide de Flamm poderá ser derivado da
forma proposta na equação 8.23. A métrica Euclidiana em coordenadas cilı́ndricas (r, ϕ, w)
é escrita,
ds2 = dw2 + dr2 + r2 dφ2 ,
(8.23)
sendo a superfı́cie descrita pela função w = w(r), pode-se escrever a métrica euclidiana
como [92],
%
ds2 = 1 +
dw
dr
2 &
dr2 + r2 dφ2 .
(8.24)
Comparando a equação 8.24 com a métrica de Schwarzschild no plano equatorial
(φ = π/2) em um tempo ﬁxo (t = constante, dt = 0), obtém-se, a equação 8.25
rs −1 2
dr + r2 dφ2 ,
ds2 = 1 −
r
(8.25)
a equação 8.25 produz uma integral para w(r), como pode ser observado na equação 8.26:
r
dr
− 1 + constante
(8.26)
= 2rs
w(r) r
rs
−1
rs
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
w = 2 rs (r − rs ),
87
(8.27)
cuja solução da equação 8.27 é o parabolóide de Flamm [91].
As caracterı́sticas referentes à simetria da métrica em questão são bem conhecidas
pois são dadas pela existência de vetores de Killing, ademais, conhece-se os vetores de
Killing de S 2 e sabe-se que há três deles. Portanto, uma variedade esfericamente simétrica
é a que tem três campos vetoriais de Killing como em S 2 [39]. O comutador dos vetores
de Killing é o mesmo em ambos os casos. Pode-se escolher os três vetores de Killing em
S 2 para serem (V (1) , V (2) , V (3) ), tais que,
[V (1) , V (2) ] = V (3)
[V (2) , V (3) ] = V (1)
[V (3) , V (1) ] = V (2) .
(8.28)
As relações de comutação são exatamente as de SO(3). Tudo o que se precisa é de
uma variedade esfericamente simétrica que possua três campos de vetores de Killing com
as supra relações de comutação. O teorema de Frobenius 2 , diz que se existe um conjunto
de campos vetoriais comutativos então existe um conjunto de funções coordenadas cujos
campos vetoriais são as derivadas parciais em relação a estas funções. Segundo o teorema,
alguns campos de vetores não comutam, mas cujo comutador fecha - o comutador de
quaisquer dois campos no conjunto é uma combinação linear de outros campos no conjunto - em seguida, as curvas integrais dos campos vetoriais envolvidos se encaixam para
descrever subvariedades da variedade em que estão todas deﬁnidas [39].
A dimensionalidade da subvariedade pode ser menor do que o número de vetores
ou mesmo igual, mas, obviamente, não maior. Dessa forma, formarão duas esferas nos
campos vetoriais que obedecerem aos vetores descritos em 8.28. Uma vez que os campos
vetoriais estendem-se por todo espaço, cada ponto estará exatamente sobre uma dessas
esferas. Dessa forma, pode-se aﬁrmar que uma variedade esfericamente simétrica pode
ser foliada em esferas [39].
Considerando-se por exemplo o espaço tridimensional euclidiano plano e considerandose a O(0, 0, 0), então R3 é claramente esfericamente simétrico em relação à rotações em
2
Teorema de Frobenius: Descreve as condições necessárias e suﬁcientes para a existência de uma
folheação por máximas variedades integrais as que cujos ﬁbrados tangentes são estendidos por uma dada
famı́lia de campos vetoriais (satisfazendo uma condição de integrabilidade) de forma parecida com uma
curva integral a qual pode ser atribuı́do um único campo vetorial.
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
88
torno da origem. Sob rotações de investigação, sob o ﬂuxo dos campos vetoriais de
Killing, pontos que se movem um para o outro, mas cada ponto permanece em uma
S 2 a uma distância ﬁxa a partir da origem [39]. Nas esferas da ﬁgura 8.1 abaixo pode-se
observar a representação pictográﬁca de esfera S 1 e S 2 . Sendo n ∈ N , deﬁne-se uma
n-esfera de raio r como sendo o conjunto de pontos em um espaço euclidiano (n + 1)dimensional que estão a uma distância r a partir de um ponto central, em que o raio
r ∈ R, S 2 = x ∈ Rn+1 : |x| = r. Nesse caso em particular tem-se uma 2-esfera, (à esquerda) ou seja, n = 2 e a 1-esfera (à direita), ou seja, n = 1.
Figura 8.1: Uma n-esfera é uma generalização da superfı́cie de uma esfera ordinária em uma dimensão
arbitrária.
São essas esferas que vão folear R3 . Naturalmente, não vão folear todo o espaço,
desde a origem em si só ﬁca colocado sob rotação - não se mover em torno de alguma
dois-esfera. Pode-se ainda ter simetria esférica sem uma ”origem” relativamente a qual
tudo rotaciona. Pode-se pensar em um Buraco de Minhoca 3 , com topologia R × S 2 .
Suprimindo-se uma dimensão e esboçando as 2-esferas como 1-esferas, o espaço terá o
aspecto da ﬁgura 8.2 [94],
z(r)[1] = int(sqrt(2 ∗ r ∗ M − 4 ∗ M 2 )/(−r + 2 ∗ M ), r);
z(r)[2] = int(−sqrt(2 ∗ r ∗ M − 4 ∗ M 2 )/(−r + 2 ∗ M ), r)
√
z(r)1 = −2 2rM − 4M 2
√
z(r)2 = 2 2rM − 4M 2
3
(8.29)
(8.30)
Deﬁnição de buraco de Minhoca Lorentziano: Se um espaço-tempo de Minkowski contém uma região
Ω compacta, e se a topologia de Ω é da forma Ω R × Σ, em que Σ é uma 3-variedade de topologia não
trivial, cujo bordo tem a topologia da forma ∂Σ S 2 , e se, além disso, as hipersuperfı́cies Σ são todas do
tipo espacial, então a região Ω contém um buraco de Minhoca intra-universo quase permanente [?].
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
89
Figura 8.2: Paraboloide de Flamm, com a topologia com topologia R × S 1 , (cilindro topológico). O
buraco negro de Schwarzschild é um reﬂexo da geometria de Schwarzschild normal. Não há buraco branco,
apenas um buraco negro e seu reﬂexo [95].
plot3d(subs(M = 1, r = sqrt(x2 + y 2 ), rhs()), subs(M = 1, r = sqrt(x2 + y 2 ), rhs(“)), x =
−10..10, y = −10..10, axes = boxed, style = P AT CHCON T OU R, grid = [100, 100], title =
‘BuracoN egrodeSchwarzschild‘)
Figura 8.3: Gráﬁco do Buraco negro de Schwarzschild, gerado pelo software Maple.
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
8.3
90
Buraco Negro de Kerr
A métrica de Schwarzschild descreve o espaço-tempo em torno de uma massa
esférica, que não tem qualquer momento angular, não obstante, a métrica de Kerr mais
geral, descreve o espaço-tempo em torno de uma massa esférica que tem um momento
angular, tal como um buraco negro rotativo.
Em suma, corresponde a métrica de Kerr às soluções das equações de campo de
Einstein para o vácuo com simetria axial e assintoticamente plano. São variados esses tipos
de solução, assegura-se a unicidade de Kerr pelo fato de proporcionar um espaço-tempo
assintoticamente Minkowskiano:
gμν = (1−, −1, −1, −1).
8.3.1
(8.31)
Exemplo de Solução e Plotagem dos Gráﬁcos - Buraco
Negro de Kerr
Segue abaixo a determinação da métrica de Kerr, com o tensor métrico descrito na
forma matricial, para tanto, deve-se considerar os métodos de tratamento análogos aos da
métrica de Schwarzschild, logo após será realizada a plotagem da superfı́cie mergulhada
[60].
Ao se inserir na tela do software Maple os seguintes comandos,
restart :
with(tensor) :
with(plots) :
with(linalg) :
with(dif f orms) :
coord := [t, r, theta, phi] : #sphericalcoordinates, whichwillbedesignatedintextas[0, 1, 2, 3]
gc ompts := array(symmetric, sparse, 1..4, 1..4) : #metriccomponents
gc ompts[1, 1] := −exp(2 ∗ P hi(r)) : #componentof intervalattached tod(t)2
gc ompts[2, 2] := exp(2 ∗ Lambda(r)) : #componentof intervalattachedtod(r)2
gc ompts[3, 3] := r2 : #componentof intervalattachedtod(theta)2
gc ompts[4, 4] := r2 ∗ sin(theta)2 : #componentof intervalattachedtod(phi)2
g := create([−1, −1], eval(gc ompts)) : #covariantmetrictensor
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
91
ginv := invert(g, detg ) : #contravariantmetrictensor
obtém-se a seguinte matriz, 8.35 (abaixo, pode-se acompanhar os cálculos do software).
⎛⎡
⎡
⎜⎢
⎢
⎢
⎜⎢
⎜⎢
⎢
⎢
⎢
table ⎜
⎜⎢compts = ⎢
⎜⎢
⎢
⎝⎣
⎣
⎤
2φ(r)
−e
0
0
⎛⎡
e
2Λ(r)
0
0
0
0
0
0
r2
0
0
⎡
0
0
r2 sin(θ)2
⎜⎢
⎢
⎜⎢
⎢
⎜⎢
⎢
⎜
⎢
table ⎜⎢compts = ⎢
⎢
⎜⎢
⎢
⎣
⎝⎣
⎤⎞
⎥
⎥⎟
⎥
⎥⎟
⎥
⎥⎟
⎥ , indexchar = [−1, −1]⎥⎟ . (8.32)
⎥
⎥⎟
⎥
⎥⎟
⎦
⎦⎠
⎤
−1
0
0
0
0
1
e2Λ(r)
0
0
0
0
1
r2
0
0
0
0
1
r 2 sin(θ)2
e2φ(r)
⎤⎞
⎥
⎥⎟
⎥
⎥⎟
⎥
⎥⎟
⎥ , indexchar = [1, 1]⎥⎟ .
⎥
⎥⎟
⎥
⎥⎟
⎦
⎦⎠
(8.33)
gm atrix := getc ompts(g)
⎡
⎢
⎢
⎢
table ⎢
⎢
⎢
⎣
−e
⎤
2φ(r)
0
0
e
2Λ(r)
0
0
0
0
0
0
r2
0
0
0
0
r2 sin(θ)2
⎥
⎥
⎥
,⎥
⎥.
⎥
⎦
(8.34)
coord := [t, r, theta, phi];
schc ompts := array(symmetric, sparse, 1..4, 1..4);
schc ompts[1, 1] := expand(subs(P hi(r) = −(1/2)∗ln(r)+(1/2)∗ln(r−2∗M ), gm atrix[1, 1]));
schc ompts[2, 2] := expand(subs(Lambda(r) = −(1/2) ∗ ln(1 − 2 ∗ M/r), gm atrix[2, 2]));
schc ompts[3, 3] := gm atrix[3, 3];
schc ompts[4, 4] := gm atrix[4, 4];
sch := create([−1, −1], eval(schc ompts))
⎛⎡
⎡
⎜⎢
⎢
⎜⎢
⎢
⎜⎢
⎢
⎜
⎢
table ⎜⎢compts = ⎢
⎢
⎜⎢
⎢
⎝⎣
⎣
getc ompts(sch)
−1 +
2M
r
⎤
0
0
0
0
1
1− 2M
r
0
0
0
0
r2
0
0
0
0
r2 sin θ2
⎤⎞
⎥
⎥⎟
⎥
⎥⎟
⎥
⎥⎟
⎥ , indexchar = [−1, −1]⎥⎟ . (8.35)
⎥
⎥⎟
⎥
⎥⎟
⎦
⎦⎠
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
⎡
⎢
⎢
⎢
table ⎢
⎢
⎢
⎣
−1 +
92
⎤
2M
r
0
0
0
0
1
1− 2M
r
0
0
0
0
r2
0
0
0
0
r2 sin θ2
⎥
⎥
⎥
⎥.
⎥
⎥
⎦
(8.36)
Inserindo-se os seguintes comandos,
coord := [t, r, theta, phi] :
rnc ompts := array(symmetric, sparse, 1..4, 1..4) : #‘metriccomponents
rnc ompts[1, 1] := −(1 − 2 ∗ M/r + Q2 /r2 ) : #‘coef f icientof d(t)2 ininterval
rnc ompts[2, 2] := 1/(1 − 2 ∗ M/r + Q2 /r2 ) : #‘coef f icientof d(r)2 ininterval
rnc ompts[3, 3] := gm atrix[3, 3] : #‘coef f icientof d(theta)2 ininterval
rnc ompts[4, 4] := gm atrix[4, 4] : #‘coef f icientof d(phi)2 ininterval
rn := create([−1, −1], eval(rnc ompts)); #‘Reissner − N ordstrom(RN )metric
obtem-se 8.37.
⎛⎡
⎡
2M
r
−
⎜⎢
⎢ −1 +
⎢
⎜⎢
⎢
⎜⎢
0
⎜⎢
⎢
table ⎜⎢compts = ⎢
⎢
⎜⎢
0
⎜⎢
⎢
⎣
⎝⎣
0
⎤
Q2
r2
0
0
0
0
0
0
r2
0
0
0
r2 sin(θ)2
1
2
1− 2M
+ Q2
r
r
⎤⎞
⎥⎟
⎥
⎥⎟
⎥
⎥⎟
⎥
⎥⎟
⎥
=
[−1,
−1]
,
index
⎥⎟ .
⎥
char
⎥⎟
⎥
⎥⎟
⎥
⎦⎠
⎦
(8.37)
subs(Q2 = M 2 , getc ompts(rn));
f actor([1, 1])
⎛⎡
⎡
2M
r
−
⎢ −1 +
⎜⎢
⎜⎢
⎢
⎢
⎜⎢
0
⎢
⎜⎢
table ⎜⎢compts = ⎢
⎢
⎜⎢
0
⎢
⎜⎢
⎝⎣
⎣
0
⎤
M2
r2
0
getc ompts(rn) :
d(s)2 = %[2, 2] ∗ d(r)2 ; #RN metric
0
0
0
0
r2
0
0
0
r2 sin(θ)2
1
2
1− 2M
+ Q2
r
r
−
Digitando-se os comandos,
0
(M − r)2
r2
⎤⎞
⎥
⎥⎟
⎥
⎥⎟
⎥
⎥⎟
⎥
⎥⎟
⎥ , indexchar = [−1, −1]⎥⎟
⎥
⎥⎟
⎥
⎥⎟
⎦
⎦⎠
(8.38)
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
93
#or
d(s)2 = d(r)2 /expand((1 − rp /r) ∗ (1 − rn /r));
#secondrepresentationof expression
obtem-se as equações 8.39 abaixo.
d(s)2 =
d(s)2 =
d(r)2
1−
2M
r
+
Q2
r2
d(r)2
1 − rn
− rp
+
r
r
(8.39)
rprn
r2
Digitando-se no software Maple, os comandos abaixo,
rp := rp
rn := rn
s = Int(1/sqrt((1 − rp /r) ∗ (1 − rn /r)), r = rn ..rp )
simplif y(value(rhs(%)), radical, symbolic)
obtem-se a equação 8.40.
r−p
s=
r−n
−
(1 −
1
rp
)(1
r
−
dr
rn
)
r
1
1
1
1
rp ln(rn − rp ) − rn ln(rn − rp ) + rp ln(rp − rn ) + rn ln(rp − rn )
2
2
2
2
(8.40)
Inserindo-se os comandos abaixo, na tela do Maple,
d(r)2 /(1 − 1/r)2 = (1 + (dif f (z(r), r))2 ) ∗ d(r)2
#equalityof radialelementsof intervals, M = 1dif f (z(r), r) = solve(%, dif f (z(r), r))[1]
dsolve(%, z(r)); #embedding
obtem-se a equação 8.41.
d(r)2
d
z(r))2 )d(r)2
1 2 = (1 + (
dr
(1 − r )
√
d
2r − 1
(r) =
dr
r−1
√
√
√
z(r) = 2 2r − 1 + ln( 2r − 1 − 1) − ln( 2r − 1 + 1) +C l
(8.41)
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
94
Após a obtenção das matrizes através do Maple, pode-se plotar o gráﬁco que representa o buraco negro de Kerr, como pode ser observado na ﬁgura 8.4.
plot3d(subs(r = sqrt(x2 +y 2 ), 2∗sqrt(2∗r−1)+ln(sqrt(2∗r−1)−1)−ln(sqrt(2∗r−1)+1)),
x = −10..10, y = −10..10, axes = boxed,
style = P AT CHCON T OU R, grid = [100, 100], title = extremeRN blackhole);
#weexpressedarctanhthroughln
Figura 8.4: Gráﬁco do buraco negro de Kerr, gerado pelo software Maple.
8.4
A esfera colapsante
Um exemplo trivial de aplicação do ﬂuxo de Ricci, é a Esfera Colapsante. Seja
uma 2-esfera com um raio unitário, com a métrica habitual gc = dϕ2 + sin2 (ϕ)dθ2 e
g(t) = (1 − 2t)gc . Sabendo-se que a métrica induzida a partir de R3 para uma esfera de
√
raio r é r2 gc , pode-se supor que o mergulho pode ser dado por it (p) = p 1 − 2t, ou em
termos de parametrizações, a notação pode ser veriﬁcada na equação 8.42,
√
√
√
jt (ϕ, θ) = ( 1 − 2t sin(ϕ) cos(θ), 1 − 2t sin(ϕ) sin(θ), 1 − 2t cos(ϕ)).
(8.42)
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
95
Considerando-se que uma parametrização consiste simplesmente em mergulhar
uma fração do plano com uma métrica bona ﬁde 4 , ou seja, a representação em coordenadas
de S 2 em um 3-espaço, em particular, j0∗ (dx2 + dy 2 + dz 2 ) é exatamente gc considerada
uma métrica em (0, π) × (0, 2π) com as mesmas coordenadas. Esta é uma solução do ﬂuxo
de Ricci, simplesmente nota-se que que Rc = Kg, em que K é a curvatura gaussiana igual
à (1 − 2t)−1 . Portanto, −2Rc(g(t)) = −2g(t) = −2(1 − 2t)−1 (1 − 2t)gc = −2gc =
∂g
.
∂t
Procedendo a veriﬁcação deve-se calcular jt∗ (dx2 , dy 2 , dz 2 ), assim segue que
√
√
√
dx = d( 1 − 2t sin ϕ cos θ) = 1 − 2t cos ϕ cos θdϕ − 1 − 2t sin ϕ sin θdθ, sodx2 =
(1 − 2t) cos2 (ϕ) cos2 θdϕ2 + (1 − 2t) sin2 (ϕ) sin2 θdθ2 − cos ϕ cos θ sin ϕ sin θdϕdθ
dy 2 = (1−2t) cos2 (ϕ) sin2 (θ)dϕ2 +(1−2t) sin2 (ϕ) cos2 (θ)dθ2 +cos ϕ cos θ sin θdϕdθanddz 2 =
(1 − 2t) sin2 (ϕ)dϕ2
(8.43)
Realizando-se a soma dos termos d(x)2 , d(y)2 , d(z)2 , obtém-se [93]
jt∗ (dx2 , dy 2 , dz 2 ) =
(1−2t)(cos2 (ϕ) cos2 (θ)+cos2 (ϕ) sin2 (θ)+sin2 (ϕ))dϕ2 +(1−2t) sin2 (ϕ)(sin2 (θ)+cos2 (θ))dθ2
= (1 − 2t)dϕ2 + (1 − 2t) sin2 ϕdθ2 = (1 − 2t)gc
(8.44)
Pode-se pensar em uma esfera diminuindo com o tempo, com seus raios cada vez
menores proporcionais à raiz quadrada do tempo remanescente até à singularidade (t = 12 ),
√
observa-se que x possuindo uma inclinação mais ı́ngreme com x → 0, o colapso se torna
cada vez mais rápido. A ﬁgura 8.5 mostra uma imagem em corte das esferas concêntricas
espaçadas uniformemente até a singularidade. Pode-se observar ainda, que o colapso
acontece em x → 12 .
4
Vocábulo latino cujo signiﬁcado: no contexto em que se encontra autêntico.
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
96
Figura 8.5: Gráﬁco ilustrando uma 2-Esfera Colapsante, vista em corte [93].
Será utilizado um procedimento computacional para descrever a Esfera Colapsante,
analogamente ao que fora descrito pictoricamente na ﬁgura 8.6, deve-se observar entretanto, que será utilizada uma ﬁgura mergulhada em um R2 : S 1 ⊂ R2 . Obtém-se assim,
um modelo do que ocorre no momento da formação de um buraco negro.
plot[2 ∗ cos(t), 2 ∗ sin(t), t = 0..2 ∗ P i], [3 ∗ cos(t), 3 ∗ sin(t), t = 0..2 ∗ P i],
[cos(t), sin(t), t = 0..2 ∗ P i], color = red, scaling = constrained
R
Figura 8.6: Gráﬁco de uma Esfera Colapsante construı́da no software Maple .
Partindo das ideias apresentadas nos parágrafos anteriores, este capı́tulo consagrou
uma pesquisa qualitativa que, em um primeiro momento foi o desenvolvimento de uma
simulação utilizando o programa Maple de computação algébrica, para o cálculo de alguns
elementos matemáticos da Relatividade Geral, como por exemplo, os das componentes
CAPÍTULO 8. RESULTADOS E DISCUSSÕES
97
dos tensores métricos, utilizados ao longo de certos cálculos, também para obtenção das
superfı́cies mergulhadas, oriundas das soluções de Schwarzschild e Kerr. Utilizando-se de
um exemplo de aplicação do ﬂuxo de Ricci, que é a esfera colapsante pode-se observar
um modelo do comportamento de formação de uma singularidade, em última instância
a visualização do comportamento de um buraco negro, observando-se naturalmente a
topologia do problema em questão.
Capı́tulo 9
Considerações Finais
O objetivo maior deste trabalho foi ampliar os casos de estudos comparativos
entre o ﬂuxo de Ricci e a Teoria da Relatividade Geral, mais particularmente ao estudo
dos buracos negros, além de realizar um levantamento bibliográﬁco e nos capı́tulos ﬁnais,
realizar algumas visualizações com a utilização do software Maple.
O Fluxo de Ricci possui um alto nı́vel de abstração para a sua visualização entretanto, objetivando também a consecução de uma forma mais instrutiva para visualizar os
resultados em baixas dimensões, constitui-se num auxilio para o estudo e a compreenção
de fenômenos relacionados a esta ideia em si. Utiliza-se vastamente de diagramas para
mostrar como a curvatura evolui, mas não se leva em conta o formalismo matemático
necessário e consequentemente, suas possı́veis aplicações em Relatividade Geral, por exemplo, pois nesse caso tem-se o que ocorre, como ocorre e que aplicações e analogias são
possı́veis.
A utilização fı́sica dá-se por intermédio da computação cientı́ﬁca. Por meio do
mergulho, que é oriundo do formalismo matemático, pode-se primeiramente estabelecer
o problema que pode ser reconhecido devido à natureza intrı́nseca do ﬂuxo de Ricci,
considerando uma variedade ﬁxa, uma métrica a evoluir, que é uma estrutura adicional
sobre esta variedade.
Em suma, está especiﬁcando-se o modo como essas estruturas deformam-se sob a
ação do ﬂuxo de Ricci. Naturalmente pode-se visualizar isso, mostrando como uma grade
de coordenadas se torna deformada, para tanto, o Maple com seus recursos visuais se
fazem necessários.
É essencialmente o que acontece quando se desenham diagramas eurı́sticos do que
CAPÍTULO 9. CONSIDERAÇÕES FINAIS
99
está ocorrendo, por exemplo, em um buraco negro ou em um buraco de minhoca. Para
ter esse signiﬁcante e signiﬁcado deve-se levar em consideração mergulhos isométricos e
a variedade em algum espaço ambiente com uma métrica ﬁxa, o que com as ferramentas
da computação cientı́ﬁca, particularmente o Maple podem verter-se útil para estudar
propriedades geométricas ou mesmo numéricas dessas estruturas.
9.1
Sugestão para Trabalhos Futuros
Seria de interesse, como ulteriores trabalhos, ir além dos estudos aqui apresentados
por meio de simulações no software Maple.
Pode-se por exemplo, utilizar o que foi descrito relativamente ao uso do Maple
para solucionar problemas relacionados à Conjectura de geometrização de Thurston,
para soluções de equações Einstein, pois uma 3-variedade compacta é uma estrutura
matemática essencial para estudar a evolução do universo do ponto de vista gravitacional. Esta conjectura, aﬁrma que qualquer 3-variedade compacta pode ser decomposta
ao longo de 2-esferas mergulhadas e toros em domı́nios, admitindo oito tipos de estruturas
geométricas, isto é, uma solução métrica localmente homogênea.
Pode-se ainda proceder o desenvolvimento de um software especı́ﬁco para a realização de tais soluções. Dessa forma, seria possı́vel obter estudo mais detalhados sobre a
evolução das métricas e o comportamento dos buracos negros.
9.2
Produção de trabalhos
Dentre os objetivos do desenvolvimento do presente trabalho destacam-se o le-
vantamento bibliográﬁco a ﬁm de estabelecer relações entre o Fluxo de Ricci e a Teoria
da Relatividade Geral, mais particularmente ao estudo dos buracos negros. Sendo assim, segue abaixo a relação de trabalhos produzidos durante a elaboração da presente
dissertação.
Participação em Eventos:
CNMAC - Congresso de Matemática Aplicada e Computacional
Tipo de trabalho: Resumo Expandido; apresentação oral e painel
CAPÍTULO 9. CONSIDERAÇÕES FINAIS
100
Tı́tulo do Trabalho: Fluxo de Ricci, energia e entropia dos buracos negros; Um
Estudo Computacional
Local/Data do evento: Uberlândia-MG/Perı́odo de 20 a 23 de Setembro de 2011
Anais: http : //www.sbmac.org.br/cmac − se2011/f iles/programa cmac se.pdf
Resumo: http : //www.sbmac.org.br/cmac − se2011/trabalhos/P DF/265.pdf
Encontro Regional de Matemática Aplicada e Computacional - ERMAC 2012
Tipo de trabalho: Resumo Expandido; apresentação oral
Tı́tulo do Trabalho: Aplicações do Fluxo de Ricci à Teoria da Relatividade por
meio de simulações Computacionais
Local/Data do evento: Botucatu-SP/Perı́odo de 30 de maio a 1 de junho de 2012
Homepage do evento: http : //www.sbmac.org.br/eventos.php?eid = 133
II Workshop do Programa de Pós Graduação em Ciência da Computação - UNESP
Tipo de trabalho: Resumo; banner
Tı́tulo do Trabalho: Estudo de soluções para visualizações e simulações do ﬂuxo
de Ricci para estudo dos Buracos Negros
Local/Data do evento: S.J.Rio Preto-SP/Perı́odo de 19 e 20 de Abril de 2012
Publicação de Trabalhos:
Local de Publicação: Interciência & Sociedade – Revista Eletrônica - Faculdade Municipal Professor Franco Montoro - ISSN 2238-1295 On-Line / ISSN 2236-0548 Impresso
Tipo de Trabalho: Artigo - Pág. 19-26
Tı́tulo do Trabalho: Aplicações do Fluxo de Ricci à Teoria da Relatividade Geral:
Estudo dos Buracos Negros
Revista: www.f mpf m.edu.br/intercienciaesociedade/
Artigo: http : //www.f mpf m.edu.br/intercienciaesociedade/arquivos/buracosn egros.pdf
Local de Publicação: Revista Cientı́ﬁca Unilago - União das Faculdades dos Grandes
Lagos ISSN 1676-9228 - Impresso / Vol. 11 / no. 01 - Janeiro - Dezembro de 2012
Tipo de Trabalho: Artigo - Pág. 41-53
Tı́tulo do Trabalho: Breve História dos Buracos Negros
CAPÍTULO 9. CONSIDERAÇÕES FINAIS
Instituição: http : //www.unilago.com.br
Revista: http : //www.unilago.com.br/publicacoes
101
Referências Bibliográﬁcas
[1] Hamilton, R., Three-Manifolds with positive Ricci Curvature, Journal of Diﬀerential Geometry, Bethlehem, Pa., US: American Mathematical Society, Vol. 17, n.2,
p. 255-306, 1982.
[2] Morgan, J.; Tian G., Ricci Flow and the Poincaré Conjecture, American Mathematical Society, Clay Mathematics Institute, Translations of mathematical
monographs / American Mathematical Society, Providence, RI, US 2006.
[3] Eells, J.; Sampson, J. H., Harmonic mappings of Riemannian manifolds, American
Journal of mathematics, Baltimore, Md., US: American Mathematical Society,
Vol. 86, n. 1, p. 109-160, 1964.
[4] Thurston, W. P., Three-dimensional manifolds, Kleinian groups and hyperbolic geometry, Bulletin of the American Mathematical Society, Lancaster, Pa., US:
American Mathematical Society, Vol. 6, n. 3, p. 357-381, 1982.
[5] Rubinstein, J. H.; Sinclair R., Visualizing Ricci Flow of Manifolds of Revolution,
Experimental Mathematics, Boston, Mass., US: Jones and Bartlett Publishers,
Vol. 14, n. 3, p. 285-298 2005.
[6] Wheeler, J. A., Our Universe: the Know and the unknow, The Physics Teacher,
College Park, Md., US: American Association of Physics Teachers, Vol. 7, n. 1, p. 24,
1969.
[7] Hawking, S. W., A Brief History Of Time: From Big Bang To Black Holes,
Bantam Books, 2005.
REFERÊNCIAS BIBLIOGRÁFICAS
103
[8] Einstein, A., On the Electrodynamics of Moving Bodies, Annalen der Physik, Leipzig,
Alemanha, DE: Johann Ambrosius Barth Verlag, Vol. 17, p. 891-921, 1905,
doi:10.1002.
[9] Einstein A., Does the Inertia of a Body Depend Upon Its Energy Content, Annalen
der Physik, Leipzig, Alemanha, DE: Johann Ambrosius Barth Verlag, Vol. 18,
p. 639-641, 1905.
[10] Einstein, A., Die Feldgleichungen der Gravitation (The Field Equations of Gravitation), Königlich Preussische Akademie der Wissenschaften, Berlin, p. 844847, 1915.
[11] Schwarzschild, K., Über das Gravitationsfeld eines Massenpunktes nach der Einstein’schen Theorie, Sitzungsberichte der Preussischen Akademie der Wissenschaften,
Physikalisch-mathematische klasse, Reimer, Berlin, S., Vol. 3, 189-196 ﬀ., 1916.
[12] Minkowski, H., Das Relativitätsprinzip,
Annalen der Physik, Leipzig, Ale-
manha, DE: Johann Ambrosius Barth Verlag, Vol. 352, n. 15, p. 927-938, 1907/1915,
doi:10.1002.
[13] Sitter, de W.; On the curvature of space, Verhandelingen der Koninklijke
Nederlandsche Akademie van Wetenschappen, Afdeelinf natuurkunde, Amsterdam,
NL: North Holland Publishing, Vol. 20, n. 1, p. 229-243, 1917.
[14] Lanczos, C., Über eine stationäre Kosmologie im Sinne der Einsteinischen Gravitationstheorie, Zeitschrift fur physik, Berlin, DE: Deutsche Physikalische Gessellschaft, Vol. 21, p. 73-110, 1924, doi:10.1007.
[15] Eddington, A., The Mathematical Theory of Relativity, Cambridge University
Press, New York, second edition, 1924.
[16] Stoner, E. C., The Limiting Density in White Dwarfs, Philosophical Magazine,
London, Edinburgh and Dublin philosophical magazine and journal of science, Vol.
7, p. 63-70, 1929.
[17] Anderson, W., Über die Existenzmöglichkeit von kosmischem Staube in der Sonnenkorona, Zeitschrift für Physik, Berlin, DE: Deutsche Physikalische Gessellschaft, Number 4, 1937.
REFERÊNCIAS BIBLIOGRÁFICAS
104
[18] Chandrasekhar, S., The Maximum Mass of Ideal White Dwarfs, The Astrophysical
Journal, Chicago, Ill., US: University of Chicago Press, Vol. 74, p. 81-82, 1931.
[19] Kepler, S. O. F; Saraiva, M. F. O., Evolução Final das Estrelas, UFRGS, 2013.
[20] Lane, J. H., On the Theoretical Temperature of the Sun under the Hypothesis of a
Gaseous Mass Maintaining its Volume by its Internal Heat and Depending on the
Laws of Gases Known to Terrestrial Experiment;, American journal of science
and arts, New Haven, Conn., US: S. Converse, 2nd series Vol. 50, p. 57-74 1870.
[21] Landau, L. D.; Lifshitz E. M., Course of Theoretical Physics, Vol. 8, Pergamon
Press, 1960.
[22] Landau, L. D.; Lifshitz E. M., Course of Theoretical Physics, Vol. 5, Pergamon
Press, 1958.
[23] Oppenheimer, J. R.; Snyder, H., On Continued Gravitational Contraction, Physical
Review letters, New York, US: American Society of Physics, New York, US: American Institute of Physics, Vol. 56, p. 455-459, 1939.
[24] Hawking, S. W., Particle Creation by Black Holes, Communications in Mathematical Physics, New York, US: Springer Verlag, Vol. 43, p. 199-220, 1975.
[25] Hawking, S. W.; Penrose, R., The Singularities of Gravitational Collapse and Cosmology, Proceedings of the Royal Society B, London, GB: Royal Society of
London, Vol. 314 n. 1519, p. 529-548, 1970, doi:10.1098.
[26] Israel, W., Event Horizonts in static electrovac space-times, Communications in
Mathematical Physics, New York, US: Springer Verlag, Vol. 8, p. 245-260, 1968.
[27] Israel, W., Event Horizonts in static vacuum space-times, Physical Review, New
York, US: American Physical Society, Vol. 164, p. 1776-1779, 1967.
[28] Kerr, R. P., Gravitational ﬁeld of a spinning mass as an example of algebraically
special metrics, Physical Review Letters, New York, US: American Society of
Physics, New York, US: American Institute of Physics Vol. 11, p. 237-238, 1963.
REFERÊNCIAS BIBLIOGRÁFICAS
[29] Carter, B., Causal Structure in space-time,
105
General Relativity and Gravi-
tation, New York, US: Plenum Press, Vol. 1, Number 4, p. 349-391, 1971, doi:
10.1007/BF00759217.
[30] Robinson, D. C.; Muller, H.; Hagen, Z.; Seifert, H. J., Black holes in static vacuum
space-times, General Relativity and Gravitation, New York, US: Plenum Press,
Vol. 4, p. 53-78, 1973.
[31] Schmidt, M., The Rate of Star Formation, The Astrophysical Journal, Chicago,
Ill., US: University of Chicago Press, Vol. 129, p. 243, 1959.
[32] Hewish, A.; Bell, S. J.; Pilkington, J. D. H.; Scott, P. F.; Collins, R. A., Observation
of a Rapidly Pulsating Radio Source, Nature, London, GB: Macmillan Journals,
Vol. 217 p. 709-713, 1968.
[33] Misner, C. W.; Thorne, K. S.; Wheeler, J. A., Gravitation, W. H. Freeman and
Company, 1973.
[34] Wald, R. M., Quantum Filds Theory in Curved Spacetimes and Black Holes
Thermodynamics, University Chicago Press, 1994.
[35] Matsas, G. E. A., Preliminaries to Quantum Fields Theory in Curved SpaceTimes, em IX Swieca, J. A., Summer School of Particles and Fields, eds. Barata,
J., Malbouisson, A., e Novaes, S., World Scientiﬁc, Singapura, 1998.
[36] Silva, A. R. R., A Segunda Lei Generalizada da Termodinâmica, 134p. Dissertação de Mestrado, (Mestrado em Fı́sica Teória) - Instituto de Fı́sica Teórica IFT, Universidade Estadual Paulista, São Paulo, 2004.
[37] Carrol, S. M., An Introduction to General Relativity - Space-time and Geometry, Pearson Education, San Francisco, USA, 2004.
[38] Davies, P. C. W., Thermodynamics of black holes, Reports on progress in
physics, Bristol, Inglaterra, GB: Institute of Physics, Vol. 41, n. 8, p. 1313-1355,
1978.
[39] Carrol, S. M., Lecture Notes on General Relativity, Institute for Theoretical
Physics, University of California, Santa Barbara, CA 93106, 1997.
REFERÊNCIAS BIBLIOGRÁFICAS
106
[40] Penrose, R.; Floyd, R. M.,; Black Holes and Gravitational Theory, Nature, London,
GB: Macmillan Journals Vol. 236, p. 377-380, 1971.
[41] Hawking, S. W.; Ellis, G. F. R., The Large Scale Structure of Space-Time,
Cambridge University Press, 1973.
[42] Penrose, R.; Hawking S. W., A Natureza do Espaço e do Tempo, Gradiva
Publicações, 1996.
[43] Penrose, R., Techniques of Diﬀerential Topoloty in Relativity, Birkbeck College, University of London, CBMS-NSF - Regional Conference Series in Applied Mathematics,
Society for Industrial and Applied Mathematics by J. W. Arrosmith Ltda.,
Bristol, England, 1972.
[44] Chandrasekhar, S., The Mathematical Theory of Black Holes, The International
series of Monographs on Physics, Oxford University Press, Walton Street, Oxford, 1983.
[45] Carter, B., Complete Analytic Extension of the Symmetry Axis of Kerr’s Solution of
Einstein’s Equations, Physical Review Letters, New York, US: American Society
of Physics, Vol. 141, p. 1242-1247, 1966.
[46] Penrose, R., Gravitational collapse: The Role of general relativity,
Rivista del
Nuovo Cimento, Bologna, Italia, IT: Societa Italiana di Fisica, Vol. 1, p. 252-276,
1969.
[47] Bekenstein, J. D., Black Holes and Entropy, Physical, New York, US: American
Physical Society Review, Vol. D7, p. 2333-2346, 1973.
[48] Parker, B. R.; MacLeod, R. J., Black hole thermodynamics in an undergraduate
course, American journal of physics, New York, US: American Institute of
Physics, Vol. 48, 1066, 1980.
[49] Ashtekar, A.; Corichi J.; Krasnov, K., Quantum Geometry and Black Hole Entropy,
Physical Review Letters, New York, US, Vol. 80, p. 904-907, 1998.
[50] Bardeen, J. M.; Carter B.; Hawking, S. W., The Four Laws of Black Hole Mechanics,
Communications in Mathematical Physics, New York, US: Springer Verlag,
Vol. 31, p. 161-170, 1973.
REFERÊNCIAS BIBLIOGRÁFICAS
107
[51] Carter, B., Axisymmetric black hole has only two degrees of freedom, Physical
Review Letters, New York, US: American Society of Physics, Vol. 26, Number 6,
p. 331-2, 1971.
[52] Huang, K., Statistical Mechanics, second edition, John Wiley and Sons Inc.,
1963.
[53] Hawking, S. W., Black-hole evaporation, Nature, London, GB: Macmillan Journals Vol. 248, p. 30-31, 1974.
[54] Geroch, R., E. H. Kronheimer, and Penrose R.; Ideal points in space-time, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 327, n. 1571, p. 545-567, 1972.
[55] Geroch, R.; Prediction in General Relativity, Foundations of Space-Time Theories,
Minnesota Studies in the Philosophy of Science, Minneapolis: University of Minnesota Press., Vol. 8, p. 81-93, 1977.
[56] Geroch, R., and Horowitz, G.; Global Structure of Spacetimes, in S. W. Hawking
and W. Israel (eds), General Relativity: An Einstein Centenary Survey. Cambridge:
Cambridge University Press, p. 212-293, 1979.
[57] Kronheimer, E. H.; Penrose, R., On the structure of causal spaces, Mathematical
proceedings of the Cambridge Philosophical Society, Cambridge, Inglaterra ,
GB: Cambridge University Press, Vol. 63, p. 481-501, 1967.
[58] Finkelstein D., Past-Future Asymmetry of the Gravitational Field of a Point Particle,
Physical Review, New York, US: American Physical Society, Vol. 110, p. 965-967,
1958.
[59] Davies, P. C. W., and Fulling, S. A.; Radiation from Moving Mirrors and from
Black Holes, Proceedings of the Royal Society A: Mathematical, Physical and
Engineering Sciences, Vol. 356, n. 1685, p. 237-257, 1977.
[60] Tolman, R. C., Relativity, Thermodynamics and Cosmology, Dover Publications Inc., 1987.
REFERÊNCIAS BIBLIOGRÁFICAS
108
[61] Nunes, F. S. M., Elementos Básicos para a Quantização Canônica de Campos Escalares e Vetoriais, Universidade Federal do Pará - PA, 2007.
[62] Zel’dovich, Y. B., The Fate of a Star and the Evolution of Gravitational Energy
Upon Accretion, Soviet Physics Doklady, New York, US: American Institute of
Physics, Vol. 9, p. 195, 1964.
[63] Zel’dovich, Y. B.; Pitaevsky, L. P.; Popov, V. S.; Starobinsky, A. A., Pair Production
in a Field of Heavy Nuclei and in a Gravitational Field, Soviet Physics JETP, New
York, US: American Institute of Physics, Vol. 14, n. 6, p. 811-813, 1972.
[64] Zel’dovich, Y. B.; Starobinsky, A. A., Particle creation and vacuum polarization in
an anisotropic gravitational ﬁeld, Soviet Physics JETP, New York, US: American
Institute of Physics, Vol. 34, n. 6, 1159, 1972.
[65] Arfken, G. B; Weber, H. J.; Harris, F. E., Mathematical Methods for Physicists,
Seventh Edition: A Comprehensive Guide, Elsevier, 2010.
[66] Christodolou, D., Reversible and Irreversible Transformations in Black-Hole Physics,
Physical Review Letters, New York, US: American Society of Physics, Vol. 25,
1596-1597, 1970.
[67] Christodolou, D.; Ruﬃni, R., Reversible Transformations of a Charged Black Hole,
Physical Review Letters, New York, US: American Society of Physics, Vol. D4,
p. 3552-3555, 1971.
[68] Mullins, W. M., Two-dimensional motion of idealized grain boundaries, Journal of
applied physics, New York, US: American Institute of Physics, Vol. 27, p. 900-904,
1956.
[69] Chen, B. L.; Yin Le, Uniqueness and Pseudolocality Theorems of the Mean Curvature Flow, Communications in analysis and geometry, Cambridge, Mass., US:
International Press, Vol. 15, Number 3, p. 435-490, 2007.
[70] Chow, B., The Ricci Flow on the 2-sphere, Journal of Diﬀerential Geometry,
Bethlehem, Pa., US: American Mathematical Society, Vol. 33, p. 325-334, 1991.
REFERÊNCIAS BIBLIOGRÁFICAS
109
[71] Firey, W. J., Shapes of worn stones, Mathematika: Journal of pure and applied
mathematics, London, GB: University College, Department of Mathematics, Vol.
21, p. 1-11, 1974.
[72] Brakke, K. A., The Motion of a Surface by its Mean Curvature (Preliminary Informal
Notes of University Courses and Seminars in Mathematics), Mathematical Notes
- Princeton University Press, Princeton, N. J., 1978.
[73] Topping, P., Lectures on The Ricci Flow, London Mathematical Society, Lecture
Note Series 325, Cambridge University Press, 2006.
[74] Cao, H. D.; XI, P. Z., A Complete Proof of the Poincaré and Geometrization Conjectures - application of the Hamilton-Perelman theory of the Ricci ﬂow, Asian Journal
of Mathematica, Hong Kong, Vol. 10, p. 165-492, 2006.
[75] Bray, H., Proof of the Riemannian Penrose Inequality using the positive mass theorem, Journal of Diﬀerential Geometry, Bethlehem, Pa., US: American Mathematical Society, Vol. 59, p. 177-367, 2001.
[76] Perelman, G., The entropy formula for the Ricci ﬂow and its geometric applications,
Cornell University Library, arXiv:math/0211159v1, 2002.
[77] Perelman G., Ricci ﬂow with surgery on three-manifolds,
Cornell University
Library, arXiv:math/0303109v1, 2003.
[78] Perelman, G., Finite extinction time for the solutions to the Ricci ﬂow on certain
three-manifolds, Cornell University Library, arXiv:math/0307245v1, 2003.
[79] Gage, M.; Hamilton, R. S., The heat equation shrinking convez plane curves, Journal
of Diﬀerential Geometry, Bethlehem, Pa., US: American Mathematical Society,
Vol. 23, p. 69-95, 1986.
[80] Shi, Wan-Xiong, Ricci deformation of the metric on complete non-compact Riemannian manifolds, Journal of diﬀerential Geometry, Bethlehem, Pa., US: American
Mathematical Society, Vol. 30, n. 2, p. 303-394, 1989.
[81] Chow, B.; Knopf D., The Ricci Flow: An Introduction, Mathematical Surveys
and Monographs, Vol. 110, 2011.
REFERÊNCIAS BIBLIOGRÁFICAS
110
[82] Lickorish, W. B. R., A Representation of Orientable Combinatorial 3-Manifolds, Annals of Mathematics, Lawrenceville, NJ, US: Princeton University Press, Vol. 76,
N. 3, p. 531-540, 1962.
[83] Adams, C. C., The Knot Book An Elementary Introduction to the Mathematical Theory of Knots, New York: W. H. Freeman, p. 257-263, 1994.
[84] Wallace, A. H., Modiﬁcations and Cobounding Manifolds, Canadian journal of
mathematics, Toronto, Canada, CA: University of Toronto, Vol. 12, p. 503-552,
1960.
[85] Angenent, S.; Knopf, D., An Example of Neck Pinching for Ricci Flow on, Mathematical Research Letters, Cambridge, Mass., US: International Press, Vol. 11 p.
493-518, 2004.
[86] Thurston, W. P., Hyperbolic structures on 3-manifolds. I. Deformation of acylindrical
manifolds, Annals of mathematics, Lawrenceville, NJ, US: Princeton University
Press, Vol. 124, n. 2, p. 203-246, 1986.
[87] Thurston, W. P., On the Geometry and dynamics of diﬀeomorphisms of surfaces,
Bulletin of the American Mathematical Society, Lancaster, Pa., US: American
Mathematical Society, Vol. 19, n. 2, p. 417-431, 1988.
[88] Kruskal, M. D., Maximal extension of Schwarzschild metric, Physical Reveview
Vol. 119, p. 1743-1745, 1960.
[89] Buchdahl, H. A., Isotropic coordinates and Schwarzschild metric, International
Journal of Theoretical Physics, Vol. 24, p. 731-739, 1985.
[90] Weinberg, G. S., Gravitation and Cosmology: Principles and Applications
of the General Theory of Relativity, John Wiley and Sons, New York, 1972.
[91] Steane, A. M., Relativity Made Relatively Easy, Ed. Univ. Oxford, 2012.
[92] Chrusciel, P. T., An Introduction to Black Holes, Mathematical Institute and Hertford College, Oxford and LMPT, Federation Denis Poisson, Marrakech, May
2008.
REFERÊNCIAS BIBLIOGRÁFICAS
111
[93] Tiee, C., A Quick Note on Visualizing Ricci Flow, University of California, San
Diego, Department of Mathematics (UCSD), 2006.
[94] Javares, M. A., Equações de Einstein e Elementos Finitos: Um exemplo no
espaço de Schwarzschild, Dissertação de Mestrado, Ibilce - Unesp, 1998.
[95] Marccone, C., SETI via Wormholes , Center for Astrodynamics, Torino (TO),
Italy, Vol. 46, Issues 10-12, P. 633-639, 2000.