Problemas Resolvidos de Física

Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 3
CAPÍTULO 36 – A LEI DA INDUÇÃO DE FARADAY
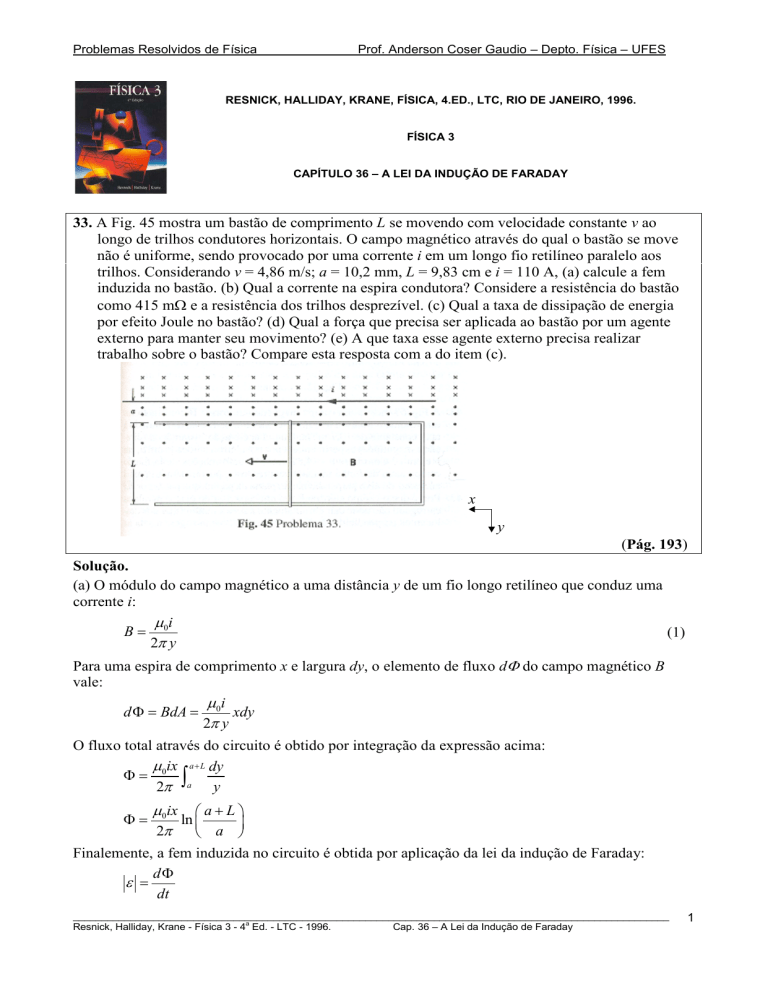
33. A Fig. 45 mostra um bastão de comprimento L se movendo com velocidade constante v ao
longo de trilhos condutores horizontais. O campo magnético através do qual o bastão se move
não é uniforme, sendo provocado por uma corrente i em um longo fio retilíneo paralelo aos
trilhos. Considerando v = 4,86 m/s; a = 10,2 mm, L = 9,83 cm e i = 110 A, (a) calcule a fem
induzida no bastão. (b) Qual a corrente na espira condutora? Considere a resistência do bastão
como 415 mΩ e a resistência dos trilhos desprezível. (c) Qual a taxa de dissipação de energia
por efeito Joule no bastão? (d) Qual a força que precisa ser aplicada ao bastão por um agente
externo para manter seu movimento? (e) A que taxa esse agente externo precisa realizar
trabalho sobre o bastão? Compare esta resposta com a do item (c).
x
y
(Pág. 193)
Solução.
(a) O módulo do campo magnético a uma distância y de um fio longo retilíneo que conduz uma
corrente i:
µi
B= 0
(1)
2π y
Para uma espira de comprimento x e largura dy, o elemento de fluxo dΦ do campo magnético B
vale:
µ 0i
Φ BdA
=
d=
xdy
2π y
O fluxo total através do circuito é obtido por integração da expressão acima:
µ ix a + L dy
Φ= 0 ∫
2π a y
Φ=
µ0ix  a + L 
ln 

2π  a 
Finalemente, a fem induzida no circuito é obtida por aplicação da lei da indução de Faraday:
dΦ
ε =
dt
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 36 – A Lei da Indução de Faraday
1
Problemas Resolvidos de Física
ε=
Prof. Anderson Coser Gaudio – Depto. Física – UFES
µ0iv  a + L 
ln 

2π  a 
(2)
=
ε 2,5279 ×10−4 A
ε ≈ 253 μV
(b) Para o cálculo da corrente induzida, pode-se considerar o circuito como sendo constituído por
uma fonte de fem ε em série com uma resistência R.
ε
i=
= 6, 0915 ×10−4 A
v
R
iv ≈ 609 μA
(c) A potência dissipada vale:
2
=
=
P Ri
1,5399 × 10−7 W
v
P ≈ 154 nW
(d) A força do agente externo pode ser obtida pela seguinte equação:
d=
Fe iv dl × B
dFe = iv dyB sen(π / 2)i
(3)
Substituindo-se (1) em (3):
 µi 
dFe = iv  0  dy.i
 2π y 
µ i i a + L dy
Fe = 0 v ∫
.i
2π a y
Fe =
µ0iv i  a + L 
ln 
i
2π
 a 
(4)
Pode-se identificar o valor de ε, (2), em (4) se multiplicarmos o segundo membro de (4) por v/v:
εi
Fe = v i
v
=
Fe
( 3,1685×10
−8
N) i
Fe ≈ ( 31, 7 nN ) i
(e) A potência do agente externo vale:
P= Fe ⋅ v
P = Fe v cos(0)
P ≈ 154 nW
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 36 – A Lei da Indução de Faraday
2