Capítulo 4
Aulas 14 a 16
Cinemática Vetorial
- Deslocamento vetorial
- Velocidade vetorial
- Aceleração vetorial
Deslocamento Vetorial
Vetor posição consiste num vetor que define a posição de
um dado corpo com referencia em um plano cartesiano.
y
r0
rf
x
r = vetor posição
Deslocamento Vetorial
Deslocamento vetorial é o vetor que determina a variação
do vetor posiçãode um corpo
y
rf
r0
-r 0
Δr
rf
Δr
x
|Δr| ≤ |ΔS|
Deslocamento Vetorial
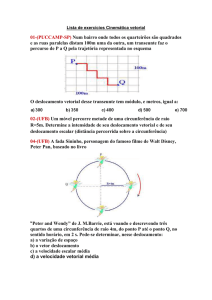
Exemplo 1
O ponteiro dos minutos de um relógio de parede tem 10 cm de
comprimento. Qual é o vetor deslocamento da extremidade do
ponteiro
a) quando ele se move de um quarto de hora para meia hora.
b) quando se move na meia hora seguinte.
c) quando se move na hora seguinte.
Velocidade
Vetorial Média
A velocidade vetorial média é a razão entre o vetor
deslocamento e o intervalo de tempo decorrido
Direção de vm é a mesma do vetor deslocamento.
Sentido de vm é o mesmo do vetor deslocamento.
Velocidade
Vetorial Média
Exemplo 2
Uma partícula desloca-se sobre a trajetória formada pelas setas
que possuem o mesmo comprimento L. A razão entre a
velocidade escalar média e a velocidade vetorial média é:
Velocidade
Vetorial Instantânea
É a medida da velocidade de um corpo quando o
intervalo de tempo é praticamente zero
r0
Δr
r0
rf
Δr
rf
Δr
r0
rf
Para um intervalo de tempo muito
pequeno o vetor deslocamento é
tangente a trajetória.
Velocidade
Vetorial Instantânea
Como o vetor velocidade tem mesma direção que o vetor
deslocamento, a velocidade instantânea é tangente a trajetória
v1
v2
v3
Em trajetória retilínea a direção da velocidade permanece constante
Em trajetória curvilínea a direção da velocidade varia a cada instante
Aceleração Vetorial
Aceleração vetorial mede a razão entre a variação do vetor
velocidade e o intervalo de tempo decorrido
Variação do módulo da velocidade
Δv
Variação da direção da velocidade
A aceleração vetorial tem a mesma direção e sentido do vetor
variação da velocidade
Aceleração Vetorial
v1
v2
v2
am
Δv
-v1
α
Aceleração Vetorial
Decomposição da aceleração vetorial
at
v
α
ac
a
at = a.cos α
ac = a.sen α
at = componente tangencial da aceleração vetorial
ac = componente centrípeta da aceleração vetorial
Aceleração Tangencial
A aceleração tangencial (aceleração escalar) indica a
variação do módulo da velocidade
at
Direção da aceleração tangencial: tangente à trajetória
mesmo da velocidade - movimento acelerado
Sentido
contrário ao da velocidade - movimento retardado
Se a aceleração tangencial for nula o movimento é uniforme
Aceleração Centrípeta
A aceleração centrípeta indica a variação na direção
do vetor velocidade
ac
Direção da aceleração centrípeta: radial (sempre perpendicular
a direção da velocidade)
Sentido da aceleração centrípeta é para o centro da trajetória
Se a aceleração centrípeta for nula o movimento é retilíneo
Velocidade
Vetorial Média
Exemplo 3
Uma partícula descreve trajetória circular, de raio r = 1,0 m, com
velocidade variável. A figura abaixo mostra a partícula em um
dado instante de tempo em que sua aceleração tem módulo, a
= 32 m/s2, e aponta na direção e sentido indicados. Nesse
instante, determine:
a) a aceleração tangencial da partícula;
b) o módulo da velocidade da partícula.