S ∆ = S – S0 ∆S>0 ∆Ss

é o ramo da Física que estuda os
movimentos. Pode ser dividida em:
a)
Cinemática: Estuda os movimentos
preocupar com as suas causas.
b)
Dinâmica: Estuda as causas dos movimentos.
c)
Estática: Estuda o estado de repouso dos corpos.
d)
Gravitação: Estuda as interações gravitacionais
assim como as suas conseqüências.
e)
Hidrostática: Estuda os fluidos em equilíbrio.
sem
S0
S0 : Posição ou espaço inicial.
S : Posição ou espaço final.
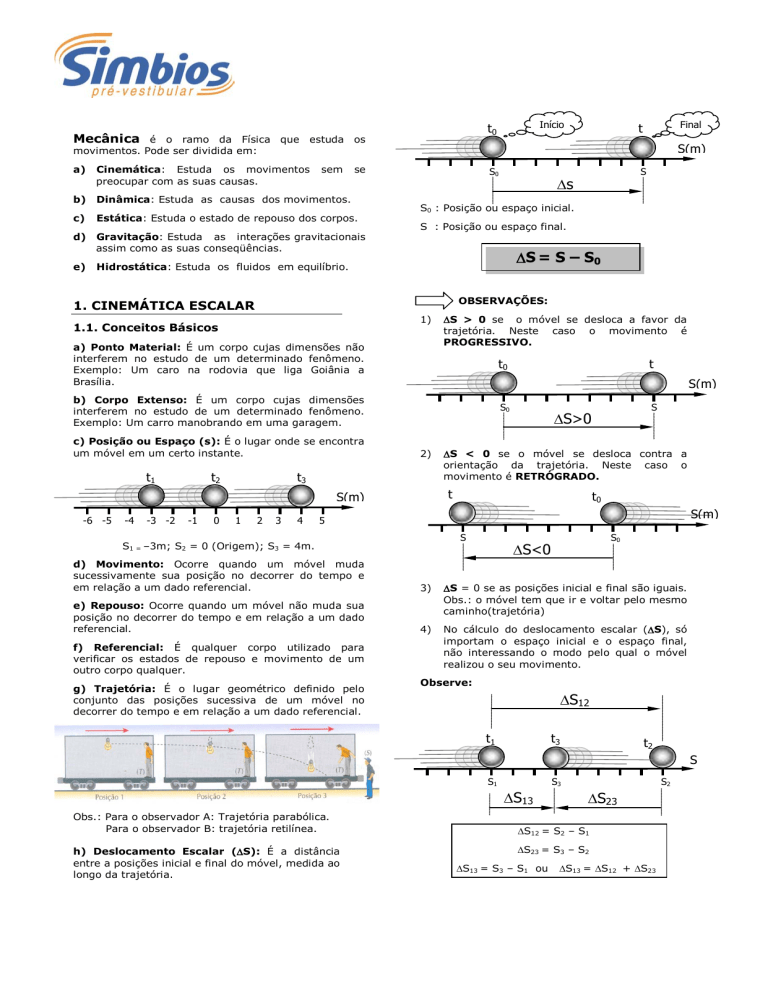
∆ S = S – S0
1)
a) Ponto Material: É um corpo cujas dimensões não
interferem no estudo de um determinado fenômeno.
Exemplo: Um caro na rodovia que liga Goiânia a
Brasília.
∆S > 0 se o móvel se desloca a favor da
trajetória. Neste caso o movimento é
PROGRESSIVO.
t0
c) Posição ou Espaço (s): É o lugar onde se encontra
um móvel em um certo instante.
t2
S0
2)
t3
-1
0
1
2
3
4
S
∆S>0
∆S < 0 se o móvel se desloca contra a
orientação da trajetória. Neste caso o
movimento é RETRÓGRADO.
t
S(m)
-3 -2
t
S(m)
b) Corpo Extenso: É um corpo cujas dimensões
interferem no estudo de um determinado fenômeno.
Exemplo: Um carro manobrando em uma garagem.
-4
S
∆s
OBSERVAÇÕES:
1.1. Conceitos Básicos
-6 -5
Final
t
S(m)
se
1. CINEMÁTICA ESCALAR
t1
Início
t0
Mecânica
t0
S(m)
5
S
S1 = –3m; S2 = 0 (Origem); S3 = 4m.
S0
∆S<0
d) Movimento: Ocorre quando um móvel muda
sucessivamente sua posição no decorrer do tempo e
em relação a um dado referencial.
3)
e) Repouso: Ocorre quando um móvel não muda sua
posição no decorrer do tempo e em relação a um dado
referencial.
∆S = 0 se as posições inicial e final são iguais.
Obs.: o móvel tem que ir e voltar pelo mesmo
caminho(trajetória)
4)
No cálculo do deslocamento escalar (∆S), só
importam o espaço inicial e o espaço final,
não interessando o modo pelo qual o móvel
realizou o seu movimento.
f) Referencial: É qualquer corpo utilizado para
verificar os estados de repouso e movimento de um
outro corpo qualquer.
g) Trajetória: É o lugar geométrico definido pelo
conjunto das posições sucessiva de um móvel no
decorrer do tempo e em relação a um dado referencial.
Observe:
∆S12
t1
t3
t2
S
S1
S3
∆S13
Obs.: Para o observador A: Trajetória parabólica.
Para o observador B: trajetória retilínea.
h) Deslocamento Escalar (∆S): É a distância
entre a posições inicial e final do móvel, medida ao
longo da trajetória.
S2
∆S23
∆S12 = S2 – S1
∆S23 = S3 – S2
∆S13 = S3 – S1 ou
∆S13 = ∆S12 + ∆S23
Sistema CGS
5) O deslocamento escalar (∆S) não deve ser
confundido com a distância efetivamente percorrida
(d). Veja o exemplo:
∆S12
Comprimento
Massa
Tempo
C
G
S
cm(centímetro)
g(grama)
s(segundo)
Sistema MK*S Técnico
t1
-6 -5
-4
t3
-3 -2
-1
0
Comprimento
t2
1
∆S13
2
3
4
5
S(m)
∆S23
M
K
m(metro)
kgf(quilograma-força)
→ ∆S23 = S3 – S2= 0 – 5 = -5m
→ ∆S13 = S3 – S1= 0 – (-3) = 3m
ou
S = 5t2 + 20t +10, no S.I.
∆S13 = ∆S12 + ∆S23 = 8 + (-5) = 3m
S = 4t3 + 10, no S.I.
Observe que as funções horárias do espaço nos
permite, sabendo-se o instante(t), determinar o
espaço(S) e sabendo-se o espaço(S), determinar o
instante(t).
Agora veja a distância percorrida entre t1 e t3:
d13 = ∆S12 + ∆S23
4. VELOCIDADE ESCALAR MÉDIA (Vm)
d13 = 13m
Uma partícula parte de uma posição (S0), no
instante (t0) e chega em uma posição (S) num instante
(t).
2. SISTEMA INTERNACIONAL
DE UNIDADES (S.I.)
t0
Grandeza
S0
S
∆S
Durante o intervalo de tempo ∆t, com ∆t = t
– t0 , a partícula apresentou um deslocamento
escalar ∆S, com ∆S = S – S0. A razão entre ∆S e ∆t
é denominada velocidade escalar média. Assim:
Unidades fundamentais do S.I.
Símbolo
t
S(m)
É um conjunto de unidades fundamentais que
é aceito universalmente e foi formulado durante a
11a Conferência de Pesos e Medidas realizada
em Paris no ano de 1960.
Nome
S
s(segundo)
Chama-se função horária do espaço toda
expressão que relaciona o espaço (S) de uma partícula
com o instante (t) qualquer do movimento.
Matemáticamente temos que S = f(t).
Exemplos:
S = 2t + 12, no S.I.
→ ∆S12 = S2 – S1= 5 – (-3) = 8m
→
Tempo
*
3. FUNÇÃO HORÁRIA DO ESPAÇO
→ S1= -3m; S2=5m; S3= 0.
d13 = 8  + -5 
Força
metro
m
comprimento
quilograma
Kg
massa
segundo
ampère
s
A
tempo
intensidade de corrente elétrica
kelvin
K
temperatura termodinâmica
mol
mol
quantidade de matéria
candela
cd
intensidade luminosa
vm =
∆S
∆t
Unidades:
→ No S.I.: m/s.
→ Outras: Km/h, cm/s,
OBSERVAÇÕES:
1) Conversão m/s ↔ km/h:
Unidades suplementares para medida de ângulos
radiano
rad
ângulo plano
esterradiano
sr
ângulo sólido
× 3,6
m/s
No estudo da Mecânica também são utilizados outros
sistemas de unidades tais como o MKS Giorgi
(subconjunto do S.I.), o CGS, o MKS técnico entre
outros.Sistema MKS Giorgi
Comprimento
Massa
Tempo
M
K
S
m(metro)
kg(quilograma)
s(segundo)
km/h
÷ 3,6
2) Se ∆S > 0 → vm > 0 → MOVIMENTO
PROGRESSIVO.
3) Se ∆S < 0 → vm < 0 → MOVIMENTO
RETRÓGRADO.
5. VELOCIDADE ESCALAR
INSTANTÂNEA (V)
Se considerarmos um intervalo de tempo
infinitamente pequeno, isto é, ∆t tendendo a zero (∆t →
0), a velocidade escalar média passa a ser a chamada
velocidade escalar instantânea (v), que representa
o valor da velocidade escalar em um determinado
instante. Assim:
v = lim
∆t → 0
EXERCÍCIOS PROPOSTOS
1. (PUC/SP)
Leia com atenção a tira da Turma da Mônica mostrada
abaixo e analise as afirmativas que se seguem,
considerando os princípios da Mecânica Clássica.
TURMA DA MÔNICA/ Maurício Souza
∆S dS
=
∆t
dt
OBSERVAÇÃO: Quando utilizamos o termo
velocidade escalar fica subentendido que essa
velocidade é a velocidade escalar instantânea.
6. ACELERAÇÃO ESCALAR MÉDIA (am)
Uma partícula sofre uma variação de velocidade ∆v, com
∆v = v – v0 , em um intervalo de tempo ∆t, com ∆t = t – t0.
A razão entre ∆v e ∆t é denominada aceleração escalar
média. Assim:
am =
∆v
∆t
Unidades:
→ No S.I.: m/s2.
→ Outras: Km/h2, cm/s2, ...
7. ACELERAÇÃO ESCALAR
INSTANTÂNEA (V)
Se considerarmos um intervalo de tempo
infinitamente pequeno, isto é, ∆t tendendo a zero (∆t →
0), a aceleração escalar média passa a ser a chamada
aceleração escalar instantânea (a), que representa
o valor da aceleração escalar em um determinado
instante. Assim:
a = lim
∆t → 0
∆v dv
=
∆t
dt
I. Cascão encontra-se em movimento em relação ao skate
e também em relação ao amigo Cebolinha.
II. Cascão encontra-se em repouso em relação ao skate,
mas em movimento em relação ao amigo Cebolinha.
III. Em relação a um referencial fixo fora da Terra, Cascão
jamais pode estar em repouso.
Estão corretas
a) apenas I
b) I e II
c) I e III
d) II e III
e) I, II e III
2. (UFMG/MG)
Júlia está andando de bicicleta, com velocidade constante,
quando deixa cair uma moeda. Tomás está parado na rua e
vê a moeda cair.
Considere desprezível a resistência do ar.
Assinale a alternativa em que melhor estão representadas
as trajetórias da moeda, como observadas por Júlia e por
Tomás.
a.
Júlia
Thomas
c.
Júlia
Thomas
b.
Júlia
Thomas
OBSERVAÇÃO: Quando utilizamos o termo
aceleração escalar fica subentendido que essa
aceleração é a aceleração escalar instantânea.
ANOTAÇÕES
d.
Júlia
Thomas
3. (Fatec/SP)
Um carro faz uma viagem de São Paulo ao Rio. Os
primeiros 250 km são percorridos com uma velocidade
média de 100 km/h. Após uma parada de 30 minutos para
um lanche, a viagem é retomada, e os 150 km restantes
são percorridos com velocidade média de 75 km/h. A
velocidade média da viagem completa foi, em km/h:
a) 60
b) 70
c) 80
d) 90
e) 100
4. (Unicamp/SP)
O Sr. P. K. Aretha afirmou ter sido seqüestrado por
extraterrestres e ter passado o fim de semana em um
planeta da estrela Alfa da constelação de Centauro. Tal
planeta dista 4,3 anos-luz da Terra. Com muita boa
vontade, suponha que a nave dos extraterrestres tenha
viajado com a velocidade da luz (3,0.108m/s), na ida e na
volta. Adote 1 ano = 3,2.107segundos. Responda:
a) Quantos anos teria durado a viagem de ida e de volta do
Sr.Aretha?
b) Qual a distância em metros do planeta à Terra?
5. (Uel/PR)
Um carro percorreu a metade de uma estrada viajando a
30km/h e, a outra metade da estrada a 60km/h. Sua
velocidade média no percurso total foi, em km/h, de
a) 60
b) 54
c) 48
d) 40
e) 30
6. (Fuvest/SP)
Um automóvel e um ônibus trafegam em uma estrada
plana, mantendo velocidades constantes em torno de 100
km/h e 75 km/h, respectivamente. Os dois veículos
passam lado a lado em um posto de pedágio. Quarenta
minutos (2/3 de hora) depois, nessa mesma estrada, o
motorista do ônibus vê o automóvel ultrapassá-lo. Ele
supõe, então, que o automóvel deve ter realizado, nesse
período, uma parada com duração aproximada de
a) 4 minutos
b) 7 minutos
c) 10 minutos
d) 15 minutos
e) 25 minutos
7. (Unicamp/SP)
"Brasileiro sofre!" Numa tarde de sexta-feira, a fila única
de clientes de um banco tem comprimento médio de 50m.
Em média, a distância entre as pessoas na fila é de 1,0m.
Os clientes são atendidos por três caixas. Cada caixa leva
3,0min para atender um cliente. Pergunta-se:
a) Qual a velocidade (média) dos clientes ao longo fila?
b) Quanto tempo um cliente gasta na fila?
c) Se um dos caixas se retirar por trinta minutos, de
quantos metros a fila aumenta?
8. (Mackenzie/SP)
Na propaganda de um modelo de automóvel, publicada
numa revista especializada, o fabricante afirmou que, a
partir do repouso, esse veículo atinge a velocidade de 100
km/h em 10 s. A aceleração escalar média nessa condição
é:
a) 2,8 m/s2
b) 3,6 m/s2
c) 10 m/s2
d) 28 m/s2
e) 36 m/s2
MOVIMENTO UNIFORME (M.U.)
V
É aquele em que a velocidade escalar
instantânea é constante e diferente de zero, de
modo que o móvel percorre espaços iguais em
intervalos de tempo iguais.
OBSERVAÇÕES:
0
t
1) Como no Movimento Uniforme a velocidade
escalar instantânea (V) é constante, ela será igual
a velocidade escalar média (Vm), ou seja:
v = vm =
2) Como a velocidade
aceleração escalar é nula.
∆S
∆t
escalar
(Repouso)
1.1) Propriedade do Diagrama V x t
não
varia
a
v
3) O M. U. pode ocorrer em qualquer tipo de
trajetória. Ela pode ser
retilínea (M.R.U.),
circular (M.C.U.)
Área
h=v
b = ∆t
0
1) DIAGRAMA VELOCIDADE X TEMPO
Como no M.U. a velocidade
constante e diferente de zero temos:
escalar
t1
t2
t
é
 Área
= b.h = ∆t.v = ∆t.
∆S
∆t
logo:
V
N
∆S =
Área
( Vxt )
OBSERVAÇÃO:
0
t
V
Á
r
(M.U. Progressivo  V > 0)
0
t1
t2
t
Á
V
0
Entre
0
e
t 1:
N
∆S1 = + Área 1
→
o
− Área 2
→
o
movimento é PROGRESSIVO.
N
Entre t1 e t2:
∆S 2 =
(M.U. Retrógrado  V < 0)
movimento é RETRÓGRADO.
 Entre 0 e t2:
OBSERVAÇÃO: O diagrama a seguir não
representa um M.U., pois, mesmo a velocidade
escalar sendo constante, ela é igual a zero e o
corpo se encontra, portanto, em repouso.
N
∆S = Área 1 − Área 2
2) FUNÇÃO HORÁRIA DO ESPAÇO DO M.U.
S = f(t)
OBSERVAÇÃO: Caso o diagrama apresente uma reta
horizontal o móvel estará em repouso, já que sua
posição permanece constante no decorrer do tempo.
Observe o esquema:
t0
3.3) PROPRIEDADE DO DIAGRAMA S X t.
t
S(m)
S0
∆S
No M.U.:
vm
S
S
S
∆S
∆S S − S 0
=
=v=
t − t0
∆t
t
t
→ tg θ = cat. oposto = ∆S
S − S0
S − S0
⇒v=
v=
t
t−0
cat. adjac.
Como
S = S 0 + v.t
⇒
∆t
0
Considerando S0 no instante t0 = 0 temos:
S − S 0 = v.t
θ
S0
OBSERVAÇÕES:
v=
∆S
∆t
temos:
∆t
N
v = tgθ
4) VELOCIDADE ESCALAR RELATIVA (Vrel)
1) S0
é a posição do móvel no instante inicial t0
= 0 e que durante o movimento não varia.
2) V é a velocidade escalar do móvel e, durante
o movimento, permanece constante (M.U.)
3) S
é a posição do móvel num instante
qualquer.
t
4) A função acima é chamada de horária porque o
espaço (S) é função do tempo (t).
5) É uma função do 1o grau já que o espaço (S)
varia linearmente em função do tempo (t)
consequentemente o diagrama S x t no M.U. é
uma reta inclidada.
3) DIAGRAMA ESPAÇO x TEMPO
3.1) Caso o movimento seja progressivo (V > 0), o
diagrama apresenta uma reta ascendente. Veja:
Definimos velocidade escalar relativa (vrel) entre
dois corpos A e B como sendo a velocidade de um em
ralação ao outro, no caso em que um deles estivesse
parado. Temos duas possibilidades: os corpos
movimentando-se no mesmo sentido e os corpos
movimentando-se em sentidos opostos.
No caso em que os corpos movimentam-se no
mesmo sentido (ver figura abaixo) sendo o corpo A
com velocidade escalar vA e o corpo B com velocidade
escalar vB o valor da velocidade escalar relativa entre
A e B (vrel) é dada por:
Vrel = |VA| – |VB|
com |VA| > |VB|.
A
S
B
∆Srel
M.U. PROGRESSIVO
S0
0
No caso em que os corpos movimentam-se em
sentidos opostos (ver figura abaixo) sendo o corpo A
com velocidade escalar vA e o corpo B com velocidade
escalar vB o valor da velocidade escalar relativa entre
A e B (vrel) é dada por:
t
3.2) Caso o movimnto seja retrógrado (V < 0), o
diagrama apresenta uma reta descendente. Veja:
Vrel = |VA| + |VB|
S
A
S0
0
B
M.U. RETRÓGRADO
t
∆Srel
E ainda...
v rel =
∆S rel
∆t
Onde:
Vrel
é a velocidade escalar relativa entre os
móveis.
∆Srel
é o deslocamento escalar relativo entre os
móveis.
∆t
é o tempo gasto para se percorrer o
deslocamento
relativo
(dR)
com
a
velocidade escalar relativa (VR).
EXERCÍCIOS PROPOSTOS
1 - (UnB/DF)
Qual é o tempo gasto para que um metrô de 200m a uma
velocidade de 180km/h atravesse um túnel de 150m? Dê
sua resposta em segundos.
2 - (Unifor/CE)
No gráfico abaixo estão representadas as abscissas de dois
móveis A e B, em função do tempo.
x(m)
B
60
50
A
20
0
5,0
t(s)
O encontro dos dois móveis ocorre no instante em
segundos, igual a:
a. 8,0
b. 10
c. 20
d. 25
e. 50
3 - (Uerj/RJ)
Um trem é composto por doze vagões e uma locomotiva;
cada vagão, assim como a locomotiva, mede 10 m de
comprimento. O trem está parado num trecho retilíneo de
ferrovia, ao lado do qual passa uma estrada rodoviária. O
tempo, em segundos, que um automóvel de 5,0 m de
comprimento, movendo-se a 15 m/s, necessita para
ultrapassar esse trem é:
a. 2,0
b. 3,0
c. 6,0
d. 8,0
e. 9,0
4 - (Uniube/MG)
Um caminhão, de comprimento igual a 20m, e um homem
percorrem, em movimento uniforme, um trecho de uma
estrada retilínea ao mesmo sentido. Se a velocidade do
caminhão é 5 vezes maior que a do homem, a distância
percorrida pelo caminhão desde o instante em que alcança
o homem até o momento em que o ultrapassa é, em m,
igual a
a. 20
b. 25
c. 30
d. 32
e. 35
5 – (ITA/SP)
Um avião voando horizontalmente a 4000m de altura numa
trajetória retilínea com velocidade constante passou por um
ponto A e depois por um ponto B situado a 3000m do
primeiro. Um observador no solo, parado no ponto
verticalmente abaixo de B, começou a ouvir o som do avião,
emitido em A, 4,00 segundos antes de ouvir o som
proveniente de B. Se a velocidade do som no ar era de
320m/s, qual era a velocidade do avião?