Pilha A segunda tarefa da nossa terceira aula foi

Pilha
A segunda tarefa da nossa terceira aula foi estudar a curva característica de uma pilha e criar um
modelo teórico para explicar o seu funcionamento.
Observamos que a tensão numa pilha é sempre 1,5V independentemente do seu tempo de uso. Então, o
que ocorre quando uma pilha fica gasta?
Montamos um circuito no qual a pilha fazia o papel de gerador. Para podermos variar a corrente, o
circuito foi composto de um resistor variável e de uma resistência de proteção para que a pilha não
entrasse em curto.
A resistência variável era um cilindro em cujo eixo havia um fio enrolado e um carrinho. Deslizando o
carrinho podíamos variar o comprimento do fio e conseqüentemente a resistência “resultante”.
Os dados foram coletados com o DataStudio. Aqui cabem duas ressalvas: a primeira é que a resistência
de proteção precisou ser muito elevada ( 100(5) Ω ) uma vez que o aparelho do DataStudio é muito
sensível.A segunda é que para a tomada dos dados a variação da resistência foi efetuada rapidamente,
para evitar erros de leitura (ruído) pelo DataStudio.
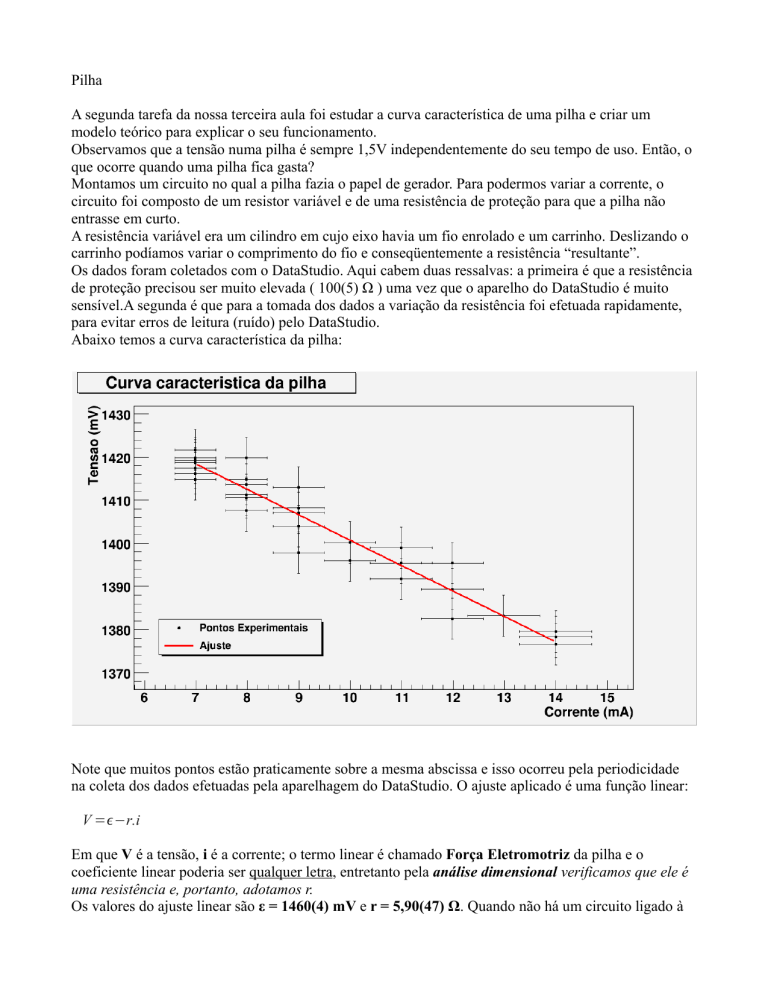
Abaixo temos a curva característica da pilha:
Note que muitos pontos estão praticamente sobre a mesma abscissa e isso ocorreu pela periodicidade
na coleta dos dados efetuadas pela aparelhagem do DataStudio. O ajuste aplicado é uma função linear:
V =−r.i
Em que V é a tensão, i é a corrente; o termo linear é chamado Força Eletromotriz da pilha e o
coeficiente linear poderia ser qualquer letra, entretanto pela análise dimensional verificamos que ele é
uma resistência e, portanto, adotamos r.
Os valores do ajuste linear são ε = 1460(4) mV e r = 5,90(47) Ω. Quando não há um circuito ligado à
pilha espera-se uma tensão em seus terminais de 1,5V indicado pelo fabricante já que a corrente, nesse
caso, é nula.
Se adotarmos a incerteza do fabricante como metade da menor divisão indicada na pilha, isto é 0,05V,
temos um valor compatível com o ε obtido pelo ajuste.
Isso é um procedimento completamente grosseiro. Mas uma vez que não haja documentação disponível
da pilha na qual a incerteza em sua tensão seja especificada, é de se esperar que o a leitura que gerou
1,5V não pudesse gerar 1,51V e, assim, a incerteza seria metade da menor divisão.
Já “r” é um resistência e é fácil ver por uma análise dimensional. Mas o que ela representa? Já que no
modelo não precisamos especificar uma corrente externa total e “r” também não é compatível com isso
já que só o resistor de proteção tinha 100(5)Ω, concluímos que “r” está associado à pilha. “r”
indicaria, portanto, uma resistência interna dependente do modo como a pilha foi construída: seus
constituintes e o arranjo utilizado.
A seguir temos o gráfico da potência fornecida pela pilha em função da corrente:
Veja que esse gráfico é no mínimo esquisito. Uma vez que nosso modelo prediz para a pilha que a
tensão é linear com a corrente, esperaríamos que o gráfico da potência (P)fosse do segundo grau, pois:
P=V.i=−r.i. i= . i−r.i2
Entretanto o gráfico é claramente linear. Então, fizemos o ajuste por três funções diferentes: uma linear,
uma parabólica e uma afim. Os resultados estão esquematizados na tabela abaixo:
Termo
quadrado
(mW/mA²)
ax²+bx+c
-0,56E-2
Tabela1 – Coeficiente dos ajustes utilizados.
Incerteza
Termo linear Incerteza
Independente Incerteza
(mW/mA²)
(V)
(V)
(mW)
(mW)
2,9 E -2
1,45
0,59
0,019
2,8
ax+b
1,34
0,06
0,54
0,55
ax
1,40
0,02
Na tabela vemos termos cujas incertezas são maiores que eles próprios: portanto o termo é
indeterminado ou o ajuste é inadequado. Assim, por exemplo, o coeficiente quadrático ou o
independente podem ser desprezados.
A melhor função é a afim (y=ax) e seu termo linear é compatível com o ε encontrado anteriormente.
Isso também acontece com os termos correspondentes a ε nos outros ajustes como era de se esperar.
Portanto, a resistência interna “r” é pequena e o termo quadrático na expressão da potência tem pouco
efeito para os valores de corrente medidos e utilizados ao longo da discussão.
Ainda pela expressão (2.0) deveria haver um máximo valor de potência para dada corrente,porém não
pudemos observá-lo. Seria interessante refazer a experiência para determiná-lo, mudando o arranjo para
isso (talvez) de modo a não utilizar o DataStudio para isso.
A tensão fornecida pela pilha é constante. Tudo indica que ela está ligada à reação química que ocorre
para gerar a corrente elétrica e isso explicaria a constância da tensão mesmo quando a pilha fica velha.
Pesquisando um pouco, encontramos uma possível explicação. A corrente fornecida é associada a
reações de oxido-redução na pilha. O número de elétrons fornecido na reação depende dos elementos
envolvidos e da concentração molar dos mesmos. Os efeitos da concentração na tensão são dados pela
Equação de Nerst:
=0−
[ Produtos]
RT
. log 
 (Forma simplificada)
nF
[ Reagentes]
Nela, R é a constante dos gases, T é a temperatura, n é o número de elétrons transferidos na reação e F
é uma constante de conversão entre as unidades Farad e Coulomb.
Então, as pilhas são construídas de modo que os elementos envolvidos e o balanceamento da equação
conservem a razão das concentrações no log no valor unitário (chamadas Condições Padrão): assim a
ddp é constante.
Além disso, a equação informa uma dependência na Temperatura o que envolveria toda uma
engenharia na construção da pilha para mantê-la constante em condições diferentes da Padrão. “ε0”
depende (em primeira aproximação) apenas dos elementos envolvidos podendo ter o mesmo valor para
reagentes diferentes. Isso é um dos motivos para umas pilhas utilizarem materiais mais tóxicos e mais
baratos, ainda sim fornecendo a mesma tensão que as “legalizadas”.
Quando a pilha pára de funcionar é porque os reagentes já foram desgastados. Entretanto, esse desgaste
se faz de modo “uniforme” mantendo o log igual a zero e, conseqüentemente, a tensão constante..