AulaP9 - Fem induzida

Força electromotriz criada por movimento
Um condutor rectangular, com R = 2,5 , desloca-se numa região onde existe um
campo magnético uniforme B = 1,7 T. A sua velocidade é v = 2,4 cm/s. Determine,
em função do tempo:
a) O fluxo através do circuito.
b) A f.e.m. induzida e a corrente no circuito.
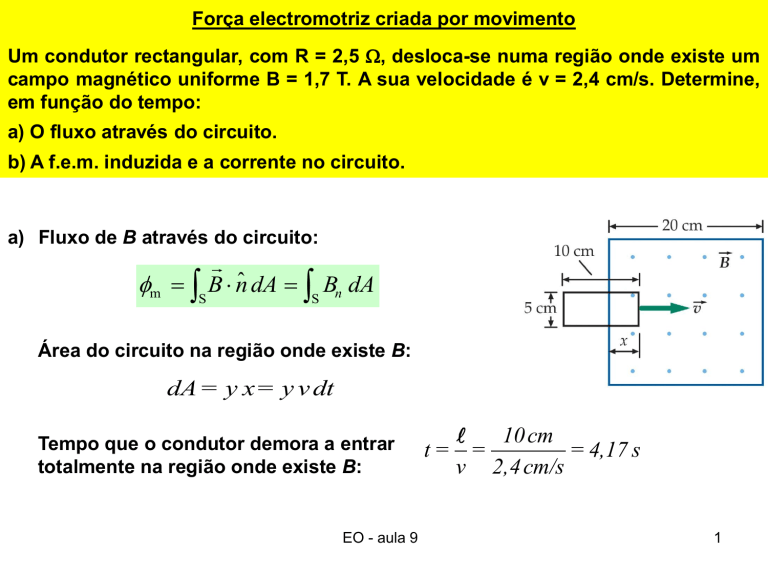
a) Fluxo de B através do circuito:
m  S B  nˆ dA  S Bn dA
Área do circuito na região onde existe B:
dA= y x= y v dt
Tempo que o condutor demora a entrar
totalmente na região onde existe B:
EO - aula 9
10 cm
t= =
= 4,17 s
v 2,4 cm/s
1
Um condutor rectangular, com R = 2,5 , desloca-se numa região onde existe um campo
magnético uniforme B = 1,7 T. A sua velocidade é v = 2,4 cm/s. Determine, em função do
tempo:
a) O fluxo através do circuito.
b) A f.e.m. induzida e a corrente no circuito.
a)
Para 0 < t < 4,17 s :
t
m =  B dA = By  v dt =  0,0024Wb/s  t
S
0
Para 4,17 s < t < 8,34 s o fluxo é
constante (o circuito começa a
sair do campo quando t=8,34 s) :
m = BA= Byx = 0,085Wb
Para 8,34 < t < 12,5 s , a área do circuito na região onde existe B
vai diminuindo (até que, para t>12,5 s, está completamente fora):
m = B A - B y
t

v dt = 0,085 - 0,0024  t - 8,34 
8,34
EO - aula 9
2
Um condutor rectangular, com R = 2,5 , desloca-se numa região onde existe um campo
magnético uniforme B = 1,7 T. A sua velocidade é v = 2,4 cm/s. Determine, em função do
tempo:
a) O fluxo através do circuito.
b) A f.e.m. induzida e a corrente no circuito.
m =  0,0024Wb/s  t
4,17 s < t < 8,34 s : m = 0,085Wb
8,34 s < t < 12,5 s : m = 0,085 - 0,0024  t - 8,34  Wb
t > 12,5 s :
m = 0
0 < t < 4,17 s :
Magnetic flux (mWb)
a)
t (s)
EO - aula 9
3
Um condutor rectangular, com R = 2,5 , desloca-se numa região onde existe um campo
magnético uniforme B = 1,7 T. A sua velocidade é v = 2,4 cm/s. Determine, em função do
tempo:
a) O fluxo através do circuito.
b) A f.e.m. induzida e a corrente no circuito.
b) Força electromotriz induzida (Lei de Faraday):
0 < t < 4,17 s :
ε = - d  0,0024 t  = -0,002V
t > 12,5 s :
ε=0
dt
d
4,17 s < t < 8,34 s : ε = -  constante  = 0
dt
ε = - d 0,085 - 0,0024  t - 8,34  
8,34 s < t < 12,5 s :
dt
=0,002V
emf (V)
d m
 =dt
t (s)
EO - aula 9
4
Força electromotriz criada por movimento
Uma barra condutora de massa m desloca-se, sem atrito, ao longo de dois carris
paralelos, ligados por uma resistência R. Os carris estão apoiados num plano
inclinado e, nesta região, existe um campo magnético B. Mostre que:
a) existe uma força F no sentido contrário ao do movimento:
b) a velocidade terminal da barra é
vt =
mgR senθ
B 2 l 2 v cos 2θ
F=
;
R
B 2l 2 cos 2θ
a) Forças que actuam na barra
enquanto desliza ao longo
do plano:
A força que se opõe ao movimento é
F  Fm cos 
com Fm = I l B , sendo I a
corrente induzida na barra como
consequência do seu movimento
no campo magnético.
EO - aula 9
5
Uma barra condutora de massa m desloca-se, sem atrito, ao longo de dois carris paralelos,
ligados por uma resistência R. Os carris estão apoiados num plano inclinado e, nesta
região, existe um campo magnético B. Mostre que:
2 2
2
a) existe uma força F no sentido contrário ao do movimento:
F=
2 2
2
b) a velocidade terminal da barra é: vt = mgR senθ B l cos θ .
a)
B l v cos θ
;
R
Força electromotriz induzida na barra:
d m
B dA
l dx
 

 B

dt
dt
dt
  B l vx   B l v cosθ
Pela lei de Ohm:
I=
ε = - B l v cosθ
R
R
 B l v cosθ 
F =
 l B cosθ =
R


B 2l 2 v
=
cos 2θ
R
EO - aula 9
6
Uma barra condutora de massa m desloca-se, sem atrito, ao longo de dois carris paralelos,
ligados por uma resistência R. Os carris estão apoiados num plano inclinado e, nesta
região, existe um campo magnético B. Mostre que:
2 2
2
a) existe uma força F no sentido contrário ao do movimento:
F=
2 2
2
b) a velocidade terminal da barra é: vt = mgR senθ B l cos θ .
b) Aplicando
 Fx  max
B l v cos θ
;
R
à barra:
B 2l 2 v
dv
m g senθ cos 2θ = m
R
dt
dv
B 2l 2 v
= g senθ cos 2θ
dt
mR
Velocidade terminal vt
vt =
dv
=0
dt
B 2l 2vt
0 = g senθ cos 2θ
mR
m g R senθ
B 2l 2 cos 2θ
EO - aula 9
7
Força electromotriz criada por movimento
Considere o problema anterior. Determine, quando a velocidade da barra for igual
à velocidade terminal:
a) a potência dissipada na resistência;
b) a taxa de variação da energia potencial da barra.
a) Potência dissipada na resistência:
 B l v cosθ 
P= R

R


b) Energia potencial:
P= RI2
2
U =mg y
dU
dy
 m g   m g vt senθ
dt
dt
EO - aula 9
8
Força electromotriz criada por movimento
Uma barra condutora de comprimento l roda em torno de um dos seus extremos
com velocidade angular constante  . A rotação é feita num plano perpendicular a
um campo magnético B. Mostre que:
a) a força magnética exercida numa carga q à distância r da extremidade fixa é
F  Bqr;
b) o potencial entre as extremidades da barra é V  B  l
2
2;
c) o fluxo através de uma área A  l 2  2 , em que    t , conduz a uma f.e.m.
B l2
induzida dada por

.
2
a) Força sobre uma carga q à distância r do ponto fixo:
F = q v× B
Como
vB
e
v= r
F = qr ωB
EO - aula 9
9
Uma barra condutora de comprimento l roda em torno de um dos seus extremos com
velocidade angular constante  . A rotação é feita num plano perpendicular a um campo
magnético B. Mostre que:
a) a força magnética exercida numa carga q à distância r da extremidade fixa é
F  Bqr;
V  B l2 2 ;
A  l 2  2 , em que    t , conduz a uma f.e.m. induzida
b) o potencial entre as extremidades da barra é
c) o fluxo através de uma área
dada por
2
  B l
2.
b) F.e.m. induzida num segmento de comprimento
dr à distância r do ponto fixo :
d m
E 
dt
 Bl v
dε = B  dr  v = B  dr  r ω = B ωr dr
Integrando esta expressão entre r=0 e r=l :
ε
l
0
0
 dε' = B ω  r dr
ε  V = 21 B ωl 2
EO - aula 9
10
Uma barra condutora de comprimento l roda em torno de um dos seus extremos com
velocidade angular constante  . A rotação é feita num plano perpendicular a um campo
magnético B. Mostre que:
a) a força magnética exercida numa carga q à distância r da extremidade fixa é
F  Bqr;
V  B l2 2 ;
A  l 2  2 , em que    t , conduz a uma f.e.m. induzida
b) o potencial entre as extremidades da barra é
c) o fluxo através de uma área
dada por
2
  B l
2.
c) Para qualquer , a área dA entre r e r+dr é
dA  r  dr
l

l
A   dA   r  dr 
0
0

1 2
l
2
r
dr
1 2
m = B A = B l θ
2
Fluxo de B na área A:
F.e.m. induzida:
dA

d  1 2  1 2 d
1
Bl   Bl
 B l 2ω
 2
dt  2
dt
2
EO - aula 9
11