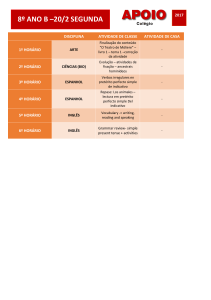
Um Estudo Sobre Espaços Vetoriais Simpléticos

Um Estudo Sobre Espaços Vetoriais Simpléticos
Fabiano Borges da Silva
∗
Lı́via T. Minami Borges
†
28 de novembro de 2015
Resumo
O presente artigo estuda de maneira detalhada espaços vetoriais que possuem
uma estrutura especial dada por uma forma bilinear simplética. A principal finalidade é descrever em detalhes a relação que existe entre as formas bilineares simpléticas e as matrizes anti-simétricas invertı́veis, fornecendo um material
acessı́vel para estudantes de graduação.
Palavras Chave: formas bilineares, espaços vetoriais simpléticos, matrizes antisimétricas.
Introdução
O objetivo deste artigo é divulgar espaços vetoriais simpléticos aos estudantes de
Álgebra Linear, afim de despertar o interesse pela área e propiciar um material que
poderá ser usado de apoio em estudos avançados de Geometria Simplética.
Espaços vetoriais simpléticos fazem parte de um contexto introdutório no estudo
da geometria das variedades simpléticas, as quais são caracterizadas pela existência
de uma 2-forma fechada e não-degenerada definida no espaço vetorial tangente da
variedade. Inicialmente, esta geometria era apenas uma ferramenta de suporte para
estudos de campos hamiltonianos em variedades. Porém, atualmente, é uma área
de pesquisa com diversas aplicações, como pode ser visto em [1] e [4].
Neste trabalho, procuramos demonstrar em detalhes os teoremas 2 ,8 e 9, que
são afirmações encontradas nos capı́tulos iniciais de [1] e [4]. Quanto ao Teorema 2,
encontramos, em [2], apenas uma versão para matrizes simétricas e, por este motivo,
fizemos sua demonstração.
1
Formas bilineares e matrizes.
Nesta seção, veremos que cada forma bilinear está associada a uma matriz e, em
particular, cada bilinear anti-simétrica está associada a uma matriz anti-simétrica.
Esta relação será importante para compreender a relação entre formas simpléticas
e matrizes anti-simétricas invertı́veis.
Definição 1 Seja V um espaço vetorial real. Uma forma bilinear sobre V é uma
função f : V × V → R que satisfaz:
∗
†
Email: [email protected], Departamento de Matemática-UNESP-Bauru/SP
Email: [email protected], Departamento de Matemática-IFSP-Birigui/SP
1
1. f (λu1 + u2 , v) = λf (u1 , v) + f (u2 , v), ∀λ ∈ R, ∀u1 , u2 , v ∈ V ;
2. f (u, λv1 + v2 ) = λf (u, v1 ) + f (u, v2 ), ∀λ ∈ R, ∀u, v1 , v2 ∈ V.
Ou seja, ela deve ser linear em cada uma das variáveis, quando a outra é deixada
fixa.
A matriz associada a uma forma bilinear f, com relação à base β = {v1 , ..., vn }
de V , é a matriz [f ]β = [aij ], onde aij = f (vi , vj ).
Para u, v ∈ V temos que u = a1 v1 + · · · + an vn e v = b1 v1 + · · · + bn vn , com
ai , bj ∈ R. E assim, pela bilinearidade da f , temos que
f (u, v) =
n X
n
X
ai bj f (vi , vj ) =
i=1 j=1
n X
n
X
ai f (vi , vj )bj .
i=1 j=1
Logo podemos escrever
f (u, v) = [u]tβ [f ]β [v]β ,
onde [v]β denota a matriz coluna formada pelas coordenadas do vetor v com relação
à base β e [u]tβ denota a transposta da matriz coluna [u]β .
Se dim V = n, o conjunto B(V, R) das formas bilineares sobre V formam um
espaço vetorial de dimensão n2 , o qual é isomorfo ao espaço vetorial das matrizes
n × n com entradas reais. De fato, se considerarmos a transformação linear
T : B(V, R) −→ Mn (R)
f
7−→ [f ]β
temos que:
(i) T é injetora. De fato, se [f ]β = [g]β para f, g ∈ B(V, R), nos vetores da base
β, temos que f (vi , vj ) = g(vi , vj ) e, para (u, v) ∈ V × V , segue que
f (u, v) =
=
n X
n
X
i=1 j=1
n X
n
X
ai bj f (vi , vj )
ai bj g(vi , vj )
i=1 j=1
= g(u, v).
(ii) T é sobrejetora. De fato, qualquer que seja A ∈ Mn (R), podemos definir
fA (u, v) = [u]tβ A[v]β e, desta maneira, temos que fA é bilinear e T (fA ) =
[fA ]β = A.
Uma forma bilinear f , tal que f (u, v) = −f (v, u), ∀ u, v ∈ V , é chamada de antisimétrica. Uma matriz A é anti-simétrica se At = −A. O próximo resultado mostra
que a bijeção mencionada acima associa formas bilineares anti-simétricas às matrizes
anti-simétricas. Mais precisamente, que o subespaço vetorial das formas bineares
anti-simétricas é isomorfo ao subespaço vetorial das matrizes anti-simétricas.
Teorema 2 Seja V um espaço vetorial real de dimensão finita e f : V × V → R
uma forma bilinear. As seguintes afirmações são equivalentes:
(a) f é anti-simétrica;
(b) [f ]β é uma matriz anti-simétrica para alguma base ordenada β de V ;
(c) [f ]γ é uma matriz anti-simétrica para toda base ordenada γ de V .
2
Demonstração. (a) ⇒ (b) Seja β uma base de V . Então, para todo u, v ∈ V , temos
[u]tβ [f ]β [v]β = f (u, v)
= −f (v, u)
= −[v]tβ [f ]β [u]β
= −([v]tβ [f ]β [u]β )t
= [u]tβ (−[f ]tβ )[v]β .
Portanto,
[f ]tβ = −[f ]β .
(b) ⇒ (c) Seja β uma base de V , tal que [f ]β é anti-simétrica. Para cada base γ
de V , existe uma matriz M invertı́vel tal que
[f ]β = M t [f ]γ M.
E assim,
([f ]β )t = (M t [f ]γ M )t = M t [f ]tγ M.
Como [f ]tβ = −[f ]β , segue que
−[f ]β = M t [f ]tγ M.
Portanto,
−M t [f ]γ M = M t [f ]tγ M.
Logo,
−[f ]γ = ([f ]γ )t .
(c) ⇒ (a) Seja β uma base de V . Então, para cada u, v ∈ V , temos que
f (u, v) = [u]tβ [f ]β [v]β . Como [u]tβ [f ]β [v]β é uma matriz 1 × 1, segue que
f (u, v) = ([u]tβ [f ]β [v]β )t
= [v]tβ ([f ]β )t [u]β
= −[v]tβ [f ]β [u]β
= −f (v, u).
2
Em [2, p.227], existe uma versão análoga à proposição acima para formas bilineares simétricas (f (u, v) = f (v, u) ∀u, v ∈ V ) e matrizes simétricas (At = A). Além
disso, como toda matriz A pode ser escrita como
1
1
A = (A + At ) + (A − At ),
2
2
temos que os subespaços das matrizes podem ser decompostos em soma direta entre
os subespaços das matrizes simétricas e anti-simétricas. A mesma decomposição
ocorre com os subespaços vetoriais das fomas bilineares, com relação às formas
simétricas e anti-simétricas.
3
2
Espaços vetoriais simpléticos.
Nesta seção, daremos uma breve introdução aos espaços vetoriais simpléticos.
Definição 3 Sejam V um espaço vetorial real e Ω : V × V → R uma forma bilinear
anti-simétrica. Dizemos que Ω é não-degenerada ou simplética se:
Ω(u, v) = 0, ∀v ∈ V ⇒ u = 0.
Um espaço vetorial simplético (V, Ω) é um espaço vetorial V , com uma forma
(ou estrutura) simplética Ω.
Para ilustrar a definição acima, daremos agora um exemplo de espaço vetorial
simplético com uma forma bilinear definida em R2 × R2 .
Exemplo 1 Seja V = R2 e considere a forma bilinear dada por
Ω0 ((u1 , u2 ), (v1 , v2 )) = u1 v2 − u2 v1 .
Mostraremos primeiramente que Ω0 é bilinear.
(i)
Ω0 (λ(u1 , u2 ) + (w1 , w2 ), (v1 , v2 )) = Ω0 ((λu1 + w1 , λu2 + w2 ), (v1 , v2 ))
= (λu1 + w1 )v2 − (λu2 + w2 )v1
= λ(u1 v2 − u2 v1 ) + (w1 v2 − w2 v1 )
= λΩ0 ((u1 , u2 ), (v1 , v2 )) + Ω0 ((w1 , w2 ), (v1 , v2 )).
(ii)
Ω0 ((u1 , u2 ), λ(v1 , v2 ) + (w1 , w2 )) = Ω0 ((u1 , u2 ), (λv1 + w1 , λv2 + w2 ))
= u1 (λv2 + w2 ) − u2 (λv1 + w1 )
= λ(u1 v2 − u2 v1 ) + (u1 w2 − u2 w1 )
= λΩ0 ((u1 , u2 ), (v1 , v2 )) + Ω0 ((u1 , u2 ), (w1 , w2 )).
Agora, vamos verificar que Ω0 é anti-simétrica.
Ω0 ((u1 , u2 ), (v1 , v2 )) = u1 v2 − u2 v1
= −(v1 u2 − v2 u1 )
= −Ω0 ((v1 , v2 ), (u1 , u2 )).
Por fim, Ω0 é simplética pois, se
Ω0 ((u1 , u2 ), (v1 , v2 )) = 0, ∀(v1 , v2 ) ∈ R2 ,
então u1 v2 − u2 v1 = 0, para todo v1 , v2 ∈ R e, portanto, u1 = u2 = 0.
De forma geral, podemos estender este exemplo tomando V = R2n e
Ω0 (u, v) = [u]tα · J0 · [v]α ,
onde
J0 =
0 I
−I 0
e I é a matriz identidade n × n. O espaço vetorial R2n , com a estrutura dada pela
forma bilinear Ω0 é chamado de espaço vetorial simplético canônico.
O conceito de isomorfismo para espaços vetoriais simpléticos é dado pela definição abaixo e será útil na compreensão do Teorema 9.
4
Definição 4 Um simplectomorfismo S entre dois espaços vetoriais simpléticos
(V1 , Ω1 ) e (V2 , Ω2 ) é um isomorfismmo linear S : V1 → V2 tal que S ∗ Ω2 = Ω1 ,
ou seja, Ω2 (S(u), S(v)) = Ω1 (u, v), para todo u, v ∈ V1 .
Afim de ilustrar a definição acima, seja Ω0 como no Exemplo 1 e Ω1 dada por
Ω1 ((u1 , u2 ), (v1 , v2 )) = 2u2 v1 − 2u1 v2 .
Podemos verificar, como foi feito no Exemplo 1, que Ω1 é uma forma simplética
1
e que S(x, y) = (− x, y) é um isomorfismo que torna (R2 , Ω0 ) e (R2 , Ω1 ) espaços
2
simplectomorfos.
3 Formas simpléticas e suas matrizes associadas.
Nesta seção, mostraremos que cada forma simplética, uma vez fixada uma base do
espaço vetorial, está associada a uma única matriz anti-simétrica e invertı́vel. Para
isso, necessitaremos dos seguintes resultados de Álgebra Linear.
Proposição 5 Sejam U e V espaços vetoriais reais de mesma dimensão e T : U →
V uma transformação linear. São equivalentes:
1. T é um isomorfismo;
2. T é injetora;
3. T é sobrejetora.
Proposição 6 Sejam U e V espaços vetoriais reais, α base de U e β base de V .
Uma transformação linear T : U → V é um isomorfismo se, e somente se, [T ]αβ for
invertı́vel, onde [T ]αβ é a matriz associada à transformação linear T.
As duas proposições acima podem ser encontradas, entre outros, em [2] e [3].
Lema 7 Sejam Ω uma forma simplética e Ω] : V → V ∗ a transformação linear
dada por Ω] (u)(v) := Ω(u, v). Então, Ω é simplética se, e somente se, Ω] é um
isomorfismo.
Demonstração. Se Ω é simplética, então o núcleo da transformação linear Ω(u, ·) é
{0} e portanto, Ω] é injetora. Pela Proposição 5, temos que Ω] é um isomorfismo.
Reciprocamente, se Ω] é um isomorfismo, como dim V = dim V ∗ , segue que Ω] é
injetora e o núcleo da transformação linear Ω(u, ·) é {0}. Portanto, Ω é simplética. 2
Quando tomamos a base canônica α = {e1 , e2 , ..., en } de V, podemos representar,
conforme visto na Seção 1, uma forma bilinear anti-simétrica Ω por uma matriz
anti-simétrica A = [Aij ], onde Aij = Ω(ei , ej ). Nestas condições, temos o seguinte
resultado.
Teorema 8 Seja Ω uma forma bilinear anti-simétrica. Então, Ω é simplética se, e
somente se, A é invertı́vel.
5
Demonstração. Pela Proposição 6 e pelo Lema 7, temos que Ω é simplética se, e
somente se, [Ω] ]αβ é invertı́vel, onde α é a base canônica e β é sua base dual. Falta
então verificar que a matriz [Ω] ]αβ coincide com a matriz At . Para isto, notemos que
Ω] (e1 ) = Ω(e1 , ·) = Ω(e1 , e1 ).e∗1 + ... + Ω(e1 , en ).e∗n ,
..
.
Ω] (en ) = Ω(en , ·) = Ω(en , e1 ).e∗1 + ... + Ω(en , en ).e∗n .
E portanto,

Ω(e1 , e1 ) · · ·

..
] α
..
[Ω ]β = 
.
.
Ω(e1 , en ) · · ·

Ω(en , e1 )

..
t
=A.
.
Ω(en , en )
2
O teorema acima permite, entre outras coisas, obter vários exemplos de formas
simpléticas a partir de matrizes anti-simétricas invertı́veis.
Exemplo 2 Considere a matriz

0
0
 0
0
A=
 −2 0
1 −1

2 −1
0 1 
.
0 0 
0 0
Como A é uma matriz invertı́vel e At = −A, segue que a forma bilinear Ω :
R4 × R4 → R associada a esta matriz é uma forma simplética. Assim, para
u = (a1 , a2 , a3 , a4 ) e v = (b1 , b2 , b3 , b4 ),
Ω(u, v) =
4 X
4
X
ai Ω(ei , ej )bj .
i=1 j=1
Ou seja, na base canônica β temos que:
Ω((a1 , a2 , a3 , a4 ), (b1 , b2 , b3 , b4 )) = [u]tβ A[v]β
= a1 (2b3 − b4 ) + a2 b4 − 2a3 b1 + a4 (b1 − b2 ).
Segue abaixo um resultado que nos fornece uma maneira de construir um espaço
vetorial simplético a partir de qualquer espaço vetorial W, de dimensão finita, e seu
espaço vetorial dual W ∗ . Além disso, dado qualquer isomorfismo linear T : W → W,
constrói-se um simplectomorfismo a partir de T e seu adjunto T ∗ .
Teorema 9 Sejam W um espaço vetorial de dimenção n e W ∗ seu dual. Então o
espaço vetorial V = W ×W ∗ possui uma estrutura simplética natural Ω : V ×V → R
definida por
Ω((u, f ), (v, g)) := g(u) − f (v).
Além disso, todo isomorfismo T : W → W determina um simplectomorfismo
T ⊕ (T −1 )∗ : V → V.
6
Demonstração. Se {e1 , e2 , ..., en } é a base canônica de W, temos que a base canônica
de V é dada por
α = {(e1 , 0), (e2 , 0), ..., (en , 0), (0, e∗1 ), (0, e∗2 ), ..., (0, e∗n )}.
Então, para todo 1 ≤ i, j ≤ n temos que:
Ω((ei , 0), (ej , 0)) = 0;
Ω((0, e∗i ), (0, e∗j )) = 0;
Ω((ei , 0), (0, e∗j )) = δij ;
Ω((0, e∗j ), (ei , 0)) = −δij .
Desta forma, como na demonstração do Teorema 8, temos que a matriz [Ω]α é
dada por:
0 −I
[Ω]α =
.
I 0
Podemos ver que [Ω]α é anti-simétrica e invertı́vel, uma vez que seu determinante
é diferente de zero. Portanto, Ω é simplética.
E ainda, T ⊕ (T −1 )∗ é um simplectomorfismo pois:
(T ⊕ (T −1 )∗ )∗ Ω((u, f ), (v, g)) = Ω((T u, (T −1 )∗ f ), (T v, (T −1 )∗ g))
= (T −1 )∗ g(T u) − (T −1 )∗ f (T v)
= g((T −1 )T u) − f ((T −1 )T v)
= gu − f v
= Ω((u, f ), (v, g)).
2
Este teorema pode ser adaptado para variedades diferenciáveis, sendo W o
espaço vetorial tangente. O leitor interessado em mais detalhes pode ver, entre
outros, [1] e [4].
7
Referências
[1] Bursztyn, H e Macarini, L. – Introdução à geometria simplética, XIV
Escola de Geometria Diferencial. Instituto de Matemática Pura e Aplicada
(IMPA), Rio de Janeiro, 2006.
[2] Coelho, F. U. e Lorenço, M. L.–Um Curso de Álgebra Linear, Editora da
Universidade de São Paulo, São Paulo, 2001.
[3] Lima, E. L.–Algebra Linear, Coleção Matemática Universitária, Instituto de
Matemática Pura e Aplicada (IMPA), Rio de Janeiro, 2011.
[4] Silva, A. C. – Introduction to symplectic and Hamiltonian geometry, Publicações Matemáticas do IMPA. [IMPA Mathematical Publications] Instituto
de Matemática Pura e Aplicada (IMPA), Rio de Janeiro, 2003.
8