comece do básico

RESOLUÇÃO COMECE DO BÁSICO - FÍSICA
SOLUÇÃO CB1.
[B]
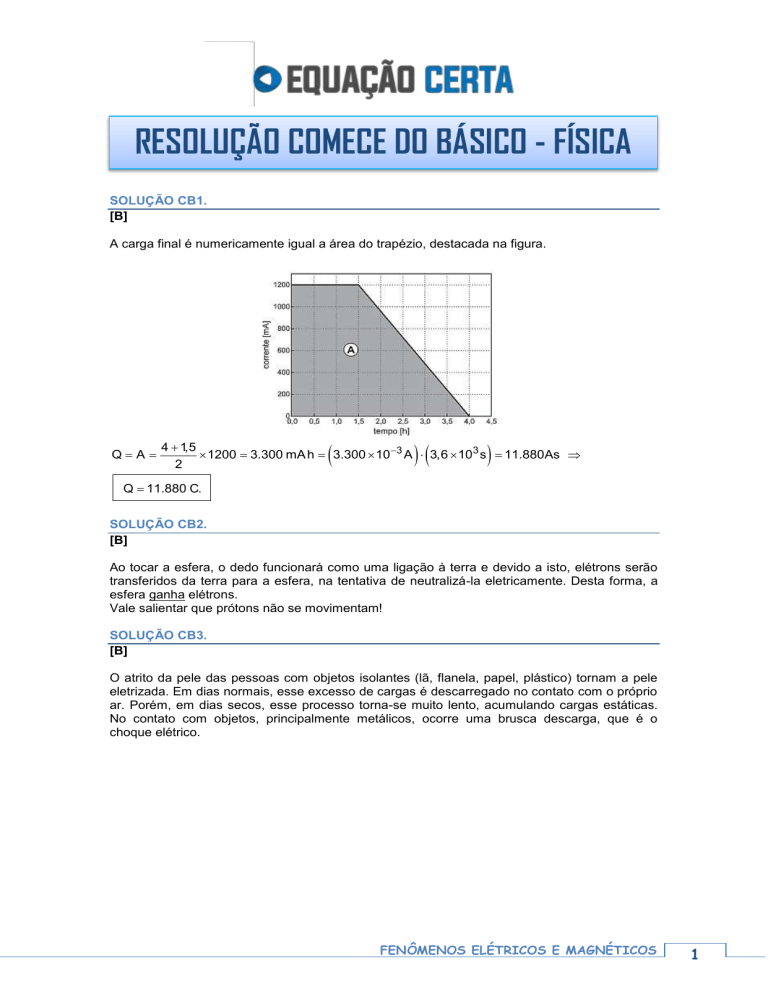
A carga final é numericamente igual a área do trapézio, destacada na figura.
QA



4  1,5
 1200  3.300 mA h  3.300  10 3 A  3,6  103 s  11.880As 
2
Q  11.880 C.
SOLUÇÃO CB2.
[B]
Ao tocar a esfera, o dedo funcionará como uma ligação à terra e devido a isto, elétrons serão
transferidos da terra para a esfera, na tentativa de neutralizá-la eletricamente. Desta forma, a
esfera ganha elétrons.
Vale salientar que prótons não se movimentam!
SOLUÇÃO CB3.
[B]
O atrito da pele das pessoas com objetos isolantes (lã, flanela, papel, plástico) tornam a pele
eletrizada. Em dias normais, esse excesso de cargas é descarregado no contato com o próprio
ar. Porém, em dias secos, esse processo torna-se muito lento, acumulando cargas estáticas.
No contato com objetos, principalmente metálicos, ocorre uma brusca descarga, que é o
choque elétrico.
FENÔMENOS ELÉTRICOS E MAGNÉTICOS
1
SOLUÇÃO CB4.
[E]
FG  FE 
G.m1.m2 K .Q1.Q2

 m1  m2  m  4,8 g  4,8.10 3 kg
2
2
d
d
Q1  Q2  Q  n.e
Substituindo os valores na equação, temos:
FG  FE 
G.m 2  k.Q 2 
Q2 
G.m 2

k
Q
G.m 2

k
Q  m.
G

k
n.e  4,8.10 3.
6,67.1011

9.109
3
4,8.10
. 6,67.1020 
3
n  2,6.10 6 elétrons
n.1,6.10 19 
SOLUÇÃO CB5.
[E]
Situação I: A força entre as esferas é dada por
F
k .3.Q 2
d2
As esferas são postas em contato e depois separadas. As esferas são idênticas, portanto, após
o contato, terão cargas iguais. Aplicando a conservação das cargas, temos:
Q
antes
 Qdepois 
Q  3Q  Q '  Q ' 
 2Q  2Q ' 
Q'  Q
Situação II: A nova força entre as esferas é dada por
k .Q 2
F '  2 , logo, observe que a nova força F’ vale F/3.
d
SOLUÇÃO CB6.
[A]
A configuração correta é apresentada na letra A. Observe que as linhas geram um contorno
saindo das cargas e o campo elétrico no ponto equidistante das duas cargas é nulo.
2
FENÔMENOS ELÉTRICOS E MAGNÉTICOS
SOLUÇÃO CB7.
[D]
Veja que o campo elétrico aponta da placa positiva para placa negativa. Assim, a placa 1 é a
placa positiva e a placa 2 é a placa negativa. Se a gota é positiva, a força elétrica será no
mesmo sentido do campo. Portanto, a partícula será desviada para o ponto C.
SOLUÇÃO CB8.
[B]
F  q.E 
F  e.E 
U  E.d 
U
E 
d
U
F  e.
d
Sendo a carga negativa a força atua contrária ao sentido do campo elétrico.
SOLUÇÃO CB9.
[B]
Segundo os conceitos sobre vetor Campo Elétrico, cargas positivas geram um campo elétrico
de afastamento e cargas negativas um campo elétrico de aproximação.
Analisando a questão em um ponto P entre o topo e a base da nuvem, tem-se o topo da
nuvem, por ser positivo, irá exercer um campo elétrico de afastamento, direção vertical e com
orientação para baixo. Como a base da nuvem é negativa, esta irá exercer um campo elétrico
que irá corroborar com o exercido com o topo.
FENÔMENOS ELÉTRICOS E MAGNÉTICOS
3
SOLUÇÃO CB10.
[B]
[I] (Verdadeira) Se a gaiola metálica for feita com tela metálica de abertura muito maior que o
comprimento de onda a blindagem torna-se ineficiente, pois a onda consegue penetrar a
gaiola.
[II] (Falsa) No interior da gaiola o campo elétrico é nulo.
[III] (Verdadeira) O papel alumínio, sendo metálico, agirá como uma gaiola de Faraday,
impedindo o recebimento de ondas eletromagnéticas, isto é, o celular não recebe
chamadas, pois o campo elétrico no interior do invólucro de alumínio é nulo.
[IV] (Falsa) As cargas se acumulam na superfície externa da gaiola.
SOLUÇÃO CB11.
[B]
[I] (Verdadeira) Se a gaiola metálica for feita com tela metálica de abertura muito maior que o
comprimento de onda a blindagem torna-se ineficiente, pois a onda consegue penetrar a
gaiola.
[II] (Falsa) No interior da gaiola o campo elétrico é nulo.
[III] (Verdadeira) O papel alumínio, sendo metálico, agirá como uma gaiola de Faraday,
impedindo o recebimento de ondas eletromagnéticas, isto é, o celular não recebe
chamadas, pois o campo elétrico no interior do invólucro de alumínio é nulo.
[IV] (Falsa) As cargas se acumulam na superfície externa da gaiola.
SOLUÇÃO CB12.
[B]
Provocando o fechamento da chave, o campo elétrico surge ao longo de todo o fio. Isso gera
um deslocamento instantâneo em todas as cargas ao longo do fio, formando a corrente
elétrica.
SOLUÇÃO CB13.
[D]
As afirmativas [I], [II], [III] e [IV] estão corretas, pois são as propriedades de um condutor em
equilíbrio eletrostático. A afirmativa [V] está incorreta, pois a esfera pode ganhar ou perder
elétrons, eletrizando-se positivamente ou negativamente.
SOLUÇÃO CB14.
[E]
Na figura, observe que o trabalho realizado pela força elétrica é nulo, no trajeto II ou no trajeto
III, pois o potencial inicial e final são os mesmos.
4
FENÔMENOS ELÉTRICOS E MAGNÉTICOS
Observa-se que a ddp entre os pontos 1 e 3 é superior à ddp entre os pontos 2 e 3, logo, o
trabalho realizado pela força elétrica da equipotencial 1 para a equipotencial 3 é superior ao
trabalho realizado da equipotencial 2 para a equipotencial 3.
Assim:
WV  q.V13 e
WI  q.V23
WV  WI
SOLUÇÃO CB15.
[A]
O campo elétrico dentro de uma esfera condutora carregada em equilíbrio eletrostático é nulo
sendo expresso por:
V  VB
U
E E A
d
d
Para esse campo ser nulo é necessário que VA  VB .
Sendo assim, o potencial elétrico dentro da esfera condutora carregada até a distância
equivalente ao raio da esfera será constante e diferente de zero, portanto a alternativa correta
é [A].
SOLUÇÃO CB16.
[A]
ΔE pel  ΔE c  0  Sistema conservativo.
ΔE pel  4.10 6 J
q.V  4.10 6
4.10 6
 2.103V
9
2.10
V  2.103V
V  
SOLUÇÃO CB17.
[A]
A expressão da Lei de Coulomb é:
F
k q1 q 2
d2
.
A intensidade da força elétrica entre duas partículas eletrizadas depende do meio, é
diretamente proporcional ao módulo do produto das cargas e inversamente proporcional ao
quadrado da distância entre elas.
FENÔMENOS ELÉTRICOS E MAGNÉTICOS
5
SOLUÇÃO CB18.
[A]
P  U .i
E  P.t
E  U .i.t
E  2,5.107.2.105.10 3
E  5.109 J
SOLUÇÃO CB19.
[B]
Se o fio 2 é três vezes maior do que o fio 1, a corrente é três vezes menor, já que a resistência
é inversamente proporcional à corrente para uma mesma ddp. Pela lei dos nós, temos no nó B:
I  I1  I 2 
I 1  3. I 2 
3.I 2  I 2  12 A
4 I 2  12 A 
I 2  3A
I1  9 A
SOLUÇÃO CB20.
[B]
Pede-se a razão entre a energia consumida pela lâmpada de LED e a lâmpada incandescente
em um consumo de 3,75 horas e 0,5 horas respectivamente. Disto,
ELED PLED  tLED 4  3,75


1
ELI
PLI  tLI
30  0,5
6
FENÔMENOS ELÉTRICOS E MAGNÉTICOS