Aula 2 - Bizuando

VI.1.1 DIFUSÃO EM FASE LÍQUIDA:
1- SOLUTO NÃO ELETROLÍTICO EM SOLUÇÕES LÍQUIDAS DILUÍDAS:
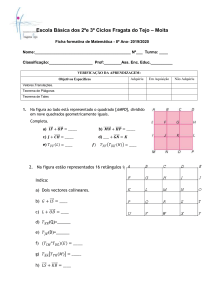
EQUAÇÃO DE Wilke e Chang (1955):
0
D AB
 B
8   M B 
 7,4  10 
T
VbA0,6
0,5
DAB  DIFUSIVIDADE. DO SOLUTO( A) NO SOLVENTE cm 2 s  ;
T  TEMPERATURA DO MEIO K  ;
VbA  VOLUME MOLAR DO SOLUTO cm 3 gmol ;
M B  MASSA MOLECULAR DO SOLVENTE g gmol  ;
  PARÂMETRO DE ASSOCIAÇÃO DO SOLVENTE
 B  VISCOSIDADE DO SOLVENTE (cP)
 ÁGUA  2,6
 ETANOL  1,5
 METANOL  1,9
PARA O RESTANTE DOS SOLVENTES:   1,0
EXEMPLO 14: ESTIME O COEFICIENTE DE DIFUSÃO DO CCl4 EM HEXANO A
25C UTILIZANDO-SE A CORRELAÇÃO DE Wilke e Chang. COMPARE O
RESULTADO COM O vALOR EXPERIMENTAL DAB = 3,70 x 10 -5 cm2/s.
DADOS: (A= CCl4 ; B=HEXANO); B=0,3 Cp.
ESPÉCIE
A=CCl4
B=hexano
Mi (g/gmol)
153, 823
86,178
(TABELA 1.2b DO CREMASCO)
Vbi (cm3/gmol)
102
140,062
2SOLUTO
NÃO
CONCENTRADAS:
ELETROLÍTICO
EM
SOLUÇÕES
LÍQUIDAS
A) CORRELAÇÃO DE Wilke (1949):
*
0
0
 AB  DAB
 x A   A  DBA
 x B   B  DAB
 AB  VISCOSIDADE DA SOLUÇÃO ELETROLÍTICA (cP)
 A  VISCOSIDADE DA SOLUÇÃO A (cP)
 B  VISCOSIDADE DA SOLUÇÃO B (cP)
x A  FRAÇÃO MOLAR DA ESPÉCIE A (cP)
x B  FRAÇÃO MOLAR DA ESPÉCIE B (cP)
0
0
DAB
, DBA
 COEF . DIFUSÃO BINÁRIA EM LÍQUIDOS EM DILUIÇÃO INFINITA (cm 2 s)
TABELA 1.6 (pg. 74 DO CREMASCO)
B) CORRELAÇÃO DE Leffler and Cullinan (1970):
 AB  D
*
AB

 A  D
  
0 xA
BA
B
D

xB
0
AB
*
DAB    DAB
  1  0,354  x A  x B
  GRADIENTE DE ATIVIDADE: REFERE-SE À CORRELAÇÃO DA NÃOIDEALIDADE DA SOLUÇÃO NO FLUXO DE MATÉRIA
EXEMPLO 15: UTILIZANDO-SE OS VALORES DOS COEFICIENTES DE
DIFUSÃO EM DILUIÇÃO PRESENTES NA TABELA 1.6 (CREMASCO), ESTIME O
DAB PARA O SISTEMA CCl4/HEXANO A 25C, NO QUAL A FRAÇÃO MOLAR DO
HEXANO É 0,43. A ESSA TEMPERATURA AS VISCOSIDADES DA SOLUÇÃO,
DO TETRACLORETO DE CARBONO E DO HEXANO SÃO, RESPECTIVAMENTE:
0,515 cP, 0,86 cP e 0,3 cP. PARA ESTE SISTEMA, O HEXANO É A ESPÉCIE A E
O CCl4 A ESPÉCIE B. COMPARE O RESULTADO OBTIDO COM O VALOR
EXPERIMENTAL 2,36 x 10-5 cm2/s E UTILIZE AS CORRELAÇÕES DE Wilke E
Leffler e Cullinan PARA ESTIMAR O VALOR DE DAB.
3- SOLUTO ELETROLÍTICO EM SOLUÇÕES LÍQUIDAS DILUÍDAS:
  z1  z 2   D1  D2 
D 

  z1  D1  z 2  D2 
0
A
DA0  COEF. DIFUSÃO EM SOLUÇÃO DILUÍDA DO ELETRÓLITO A z 2  B z1 EM UM SOLVENTE (cm 2 s)
z1 , z 2  CARGA DO ELETRÓLITO
D1 , D2  COEFICIENT E DE DIFUSÃO IÔNICA EM DILUIÇÃO INFINITA EM ÁGUA A 25C
EXEMPLO 16: DETERMINE O COEFICIENTE DE DIFUSÃO EM DILUIÇÃO
INFINITA A 25C DO NaCl, MgSO4, Na2SO4 E MgCl2 EM ÁGUA. COMPARE OS
RESULTADOS OBTIDOS COM O VALOR EXPERIMENTAL CONTIDO NA TABELA
1.9 DO CREMASCO.
4DIFUSÃO
DE
CONCENTRADAS:
ELETRÓLITOS
EM
SOLUÇÕES
CORRELAÇÃO DE Gordon (1977):
 ln    1    w

D A  D  1  m
  

m   c w  V w    AB

0
A
10
 ln  
1 m
 1   Ai  m i
m
i 1
10
i
1
2
10
A

m

A

m

A

m

....

A

m
 i
1
2
10
i 1
m
1000  w A
M A  1  w A 
c w V w  1  m  4



LÍQUIDAS
10
1   w

i  
D A  D  1   Ai  m   
  
i 1

  c w  V w    AB
0
A



m  MOLALIDADE ( gmol SOLUÇÃO Kg SOLVENTE)
wA  FRAÇÃO MÁSSICA DO SOLUTO ( Kg SOLUTO Kg SOLUÇÃO)
M A  MASSA MOLECULAR DO SOLUTO ( g gmol)
 AB  VISCOSIDADE DA SOLUÇÃO ELETROLÍTICA (cP)
 w  VISCOSIDADE DA ÁGUA (cP)
Vw  VOLUME. PARCIAL MOLAL DA ÁGUA NA SOLUÇÃO (cm 3 gmol)
Ai  CONSTANTE PARA O ELETÓLITO (TABELADO)
DA0  COEF . DIF. A DILUIÇÃO INFINITA DO SOLUTO EM ÁGUA A 25C (TABELADO)
EXEMPLO 17: ESTIME O COEFICIENTE DE DIFUSÃO DO SAL DE COZINHA A
25C EM ÁGUA. A FRAÇÃO MÁSSICA DO SAL É IGUAL A 0,15. COMPARE O
VALOR OBTIDO COM O VALOR EXPERIMENTAL DE 1,538 x 10-5 cm2/s.
DADOS: w=0,894 cP; AB=1,20 cP; D0A =1,612 x 10-5 cm2/s (TABELA 1.9)
VI.1.2 DIFUSÃO EM SÓLIDOS CRISTALINOS:
SÓLIDO CRISTALINO NÃO POROSO  ÁTOMOS MAIS PRÓXIMOS ENTRE
SI DO QUE EM QUALQUER OUTRO ESTADO DA MATÉRIA. NESTE CASO, O
COEFICIENTE DE DIFUSÃO É DADO POR:
D AB  D0  e
 Q 


 RT 
D0  COEF. DIF. SEM QUE HOUVESSE NECESSIDADE DO SALTO ENERGÉTICO (cm2/s);
(TABELA 1.13 DO CREMASCO)
R
CONSTANTE UNIVERSAL DOS GASES (1,987 cal/mol.K);
Q  ENERGIA DE ATIVAÇÃO DIFUSIONAL (cal/mol);
T
TEMPERATURA ABSOLUTA (K).
EXEMPLO 18: ESTIME A DIFUSIVIDADE DO CARBONO EM Fe (ccc) E EM Fe
(cfc) A 1000C.
DIFUSÃO EM SÓLIDOS POROSOS:
UM SÓLIDO POROSO APRESENTA DISTRIBUIÇÃO (OU NÃO) DE POROS E
GEOMETRIA INTERNA E EXTERNA PECULIARES QUE DETERMINAM A
MOBILIDADE DO DIFUNDENTE. EM FACE DISTO, TEM-SE A SEGUINTE
CLASSIFICAÇÃO:
A- DIFUSÃO DE FICK OU ORDINÁRIA;
B- DIFUSÃO DE KNUDSEN;
C- DIFUSÃO CONFIGURACIONAL.
A- DIFUSÃO DE FICK OU ORDINÁRIA: PARA GASES DENSOS SE
DIFUNDINDO PARA O INERIOR DE UM SÓLIDO QUE APRESENTA POROS
RELATIVAMENTE GRANDES (OU SEJA, MAIOR QUE O CAMINHO LIVRE MÉDIO
DAS MOLÉCULAS DIFUNDENTES):
Def  D AB
P


APARECE EM FUNÇÃO DA NATUREZA TORTUOSA
DO SÓLIDO POROSO
Def  f T , P,  P , 
Def 
COEFICIENTE EFETIVO DE DIFUSÃO (cm2/s);
D AB 
P 

COEFICIENTE DE DIFUSÃO DA ESPÉCIE A NA ESPÉCIE B (cm2/s);
POROSIDADE DO SÓLIDO;
TORTUOSIDADE.
TABELADOS
B- DIFUSÃO DE KNUDSEN: PARA GASES LEVES, À PRESSÃO
SUFICIENTEMENTE BAIXA SE DIFUNDINDO PARA O INERIOR DE UM SÓLIDO
QUE APRESENTA POROS ESTREITOS (DA ORDEM DO CAMINHO LIVRE MÉDIO
DO DIFUNDENTE)  COLISÕES ENTRE AS MOLÉCULAS DESPREZÍVEIS NO
FENÔMENO
DIFUSIVO
E
CADA
ESPÉCIE
QUÍMICA
DIFUNDE
INDEPENDENTEMENTE DAS DEMAIS. NESTE CASO A DIFUSIVIDADE É DADA
POR:
 T 

DK  9,7  10 rP 
MA 
3
1
2
2 P
2  VP
rP 

S  B
S
rP  RAIO MÉDIO DOS POROS cm ;
S  ÁREA SUP. ESPECÍFICA DA MATRIZ POROSA cm 2 g ;
 B  MASSA ESPECÍFICA DO SÓLIDO g cm 3 ;
VP  VOL. ESPECÍFICO DO PORO DA PART . SÓLIDA cm 3 g .
QUANDO A TORTUOSIDADE É CONSIDERADA NA DIFUSÃO DE KNUDSEN, O
COEFICIENTE DE DIFUSÃO É CORRIGIDO PELA SEGUINTE EQUAÇÃO:
DK ef
P
 DK 

A ESTRUTURA COMPLEXA DE UM SÓLIDO POROSO FAZ COM QUE UM
SOLUTO GASOSO, SE DEPARE COM VÁRIOS TAMANHOS DE POROS,
CARACTERIZANDO TANTO A DIFUSÃO ORDINÁRIA QUANTO A DE KNUDSEN.
NESTE CASO, UTILIZA-SE A SEGUINTE EQUAÇÃO:
1
1
1


D A ef
Def DK ef


DA ef  COEFICIENTE DIFUSIVO CONSIDERANDO AS LEIS DE FICK E KNUDSEN cm 2 s .
EXEMPLO 19: DETERMINE O COEFICIENTE DE DIFUSÃO EFETIVO DO
DIÓXIDO DE CARBONO EM UMA PARTÍCULA CATALÍTICA ESFÉRICA DE
ALUMINA A 30C, UTILIZANDO OS DADOS APRESENTADOS NA TABELA 1.14
DO CREMASCO.
C- DIFUSÃO CONFIGURACIONAL: OCORRE EM MATERIAIS CONHECIDOS
COMO “zeólitas” QUE SÃO MATERIAIS CONSTITUÍDOS POR UMA REDE
REGULAR DE MICROPOROS COM DIÂMETRO INFERIOR A 1 nm.
CERCA DE 1.000.000.000.000
DE POROS / mm2
 MOLÉCULAS DE DIFERENTES TAMANHOS PODEM SER SEPARADAS
ATRAVÉS DOS MICROPOROS, EM UM PROCESSO QUE PODERIA SER
DESCRITO COMO UM PENEIRAMENTO MOLECULAR.
QUANDO O DIÂMETRO DO PORO APRESENTA A MESMA GRANDEZA DAQUELE
ASSOCIADO AO DIFUNDENTE, TEM-SE A DIFUSÃO CONFIGURACIONAL:
D AZEO  D0  e
 Q 


 RT 
D0  COEF. EFETIVO DE DIFUSÃO EM ZEÓLITAS (cm2/s);
R
CONSTANTE UNIVERSAL DOS GASES (1,987 cal/mol.K);
Q  ENERGIA DE ATIVAÇÃO DIFUSIONAL (cal/mol);
T
TEMPERATURA ABSOLUTA (K).
D AZEO 
COEF. EFETIVO DE DIFUSÃO SO SOLUTO NA ZEÓLITA (cm2/s).