Recredenciamento Portaria MEC 347, de 05.04.2012

Recredenciamento
Portaria MEC 347, de 05.04.2012 - D.O.U. 10.04.2012.
Disciplina de Álgebra I
Algoritmos /Quest(xii)
Grafos e Ciclos Hamiltonianos
Um problema aparentemente similar ao dos grafos eulerianos é o de
procurar em G um caminho fechado que passe por todos os vértices uma
e só uma vez. Um caminho assim teria de ser necessariamente um ciclo;
chamamos um tal ciclo de ciclo hamiltoniano. O nome é em homenagem
a Sir Willian R. Hamilton, matemático irlandês que estudou e divulgou o
problema, embora a primeira formulação tenha sido feita por Kirkman em
1885. As primeiras denotações de grafo hamiltoniano e de grafo semihamiltoniano seguem as mesmas diretrizes dos grafos eulerianos. Um
grafo e seu ciclo hamiltoniano aparecem na figura (a); um grafo semihamiltoniano aparece na figura (b).
O Problema do Caixeiro Viajante
Embora semelhante ao problema do cálculo do circuito euleriano, o
ciclo hamiltoniano é muito mais complexo, pois não são conhecidas todas
as condições necessárias e suficientes para que um grafo genérico
contenha um ciclo hamiltoniano nem tampouco métodos eficientes para
construir tal ciclo.
Este problema está intimamente relacionado ao problema do caixeiro
viajante, o qual consiste em encontrar um caminho que passe por todas
as cidades uma única vez e retorne ao ponto de partida, escolhendo para
isso um caminho de custo mínimo. Este caminho consiste em um ciclo
hamiltoniano de custo mínimo, onde a soma dos custos das arestas
pertencentes ao ciclo é mínima. O problema do caixeiro viajante é um
dos problemas mais estudados no campo da pesquisa operacional, mas até
hoje não foi encontrado um algoritmo computacionalmente eficiente para
resolvê-lo. Sua formulação é simples: dado um grafo completo valorado
G, desejamos determinar o valor do menor ciclo hamiltoniano de G.
Tomemos o exemplo dado pela seguinte matriz valorada de adjacência:
(a)
(b)
Então, como vimos na figura (a), Um grafo G é chamado
Hamiltoniano quando possui um ciclo que inclui todos os vértices de G,
ou seja, neste ciclo cada vértice aparece uma única vez, com exceção do
vértice de partida. Como vimos no exemplo (b), se o grafo não contiver
um ciclo hamiltoniano, mas contiver um caminho entre dois vértices de
forma que cada vértice do grafo seja visitado uma única vez, então este
grafo é chamado semi-hamiltoniano.
Exercícios I
1) Os grafos (c) e (d) abaixo são, cada um, separadamente, hamiltoniano?
Semi-hamiltoniano? É euleriano ou semi-euleriano?
(c)
(d)
(c): ___________________________________________________
(d): ___________________________________________________
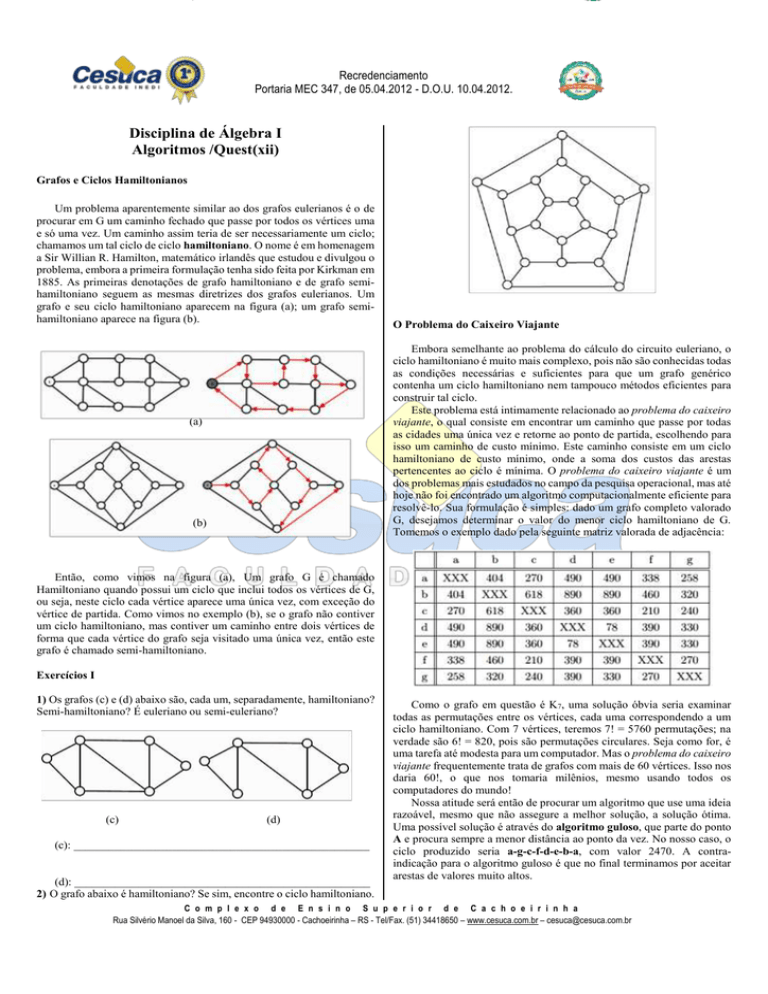
2) O grafo abaixo é hamiltoniano? Se sim, encontre o ciclo hamiltoniano.
Como o grafo em questão é K7, uma solução óbvia seria examinar
todas as permutações entre os vértices, cada uma correspondendo a um
ciclo hamiltoniano. Com 7 vértices, teremos 7! = 5760 permutações; na
verdade são 6! = 820, pois são permutações circulares. Seja como for, é
uma tarefa até modesta para um computador. Mas o problema do caixeiro
viajante frequentemente trata de grafos com mais de 60 vértices. Isso nos
daria 60!, o que nos tomaria milênios, mesmo usando todos os
computadores do mundo!
Nossa atitude será então de procurar um algoritmo que use uma ideia
razoável, mesmo que não assegure a melhor solução, a solução ótima.
Uma possível solução é através do algoritmo guloso, que parte do ponto
A e procura sempre a menor distância ao ponto da vez. No nosso caso, o
ciclo produzido seria a-g-c-f-d-e-b-a, com valor 2470. A contraindicação para o algoritmo guloso é que no final terminamos por aceitar
arestas de valores muito altos.
C o m p l e x o d e E n s i n o S u p e r i o r d e C a c h o e i r i n h a
Rua Silvério Manoel da Silva, 160 - CEP 94930000 - Cachoeirinha – RS - Tel/Fax. (51) 34418650 – www.cesuca.com.br – [email protected]
Recredenciamento
Portaria MEC 347, de 05.04.2012 - D.O.U. 10.04.2012.
Na figura abaixo, por exemplo, temos um grafo completo, valorado
nas arestas, e desejamos encontrar o ciclo hamiltoniano com menor valor
total (problema do caixeiro viajante). Para isto, use o algoritmo guloso e
constate que o valor obtido nem sempre (ou quase nunca) é o melhor valor
(que pode ser encontrado por exame exaustivo).
(e)
Subconjuntos Especiais de um Grafo
Conjuntos Independentes
Suponhamos que um grafo represente a incompatibilidade de horários
entre professores que devem dar prova final; os vértices x e y estarão
ligados se representarem professores que têm alunos em comum para
ministrar a prova. Qual o maior número de professores que podem dar
prova ao mesmo tempo? A resposta é dada pelo subconjunto
independente máximo de vértices do grafo.
O subconjunto assinalado com quadrados negros no grafo dado a
seguir mostra um conjunto com estas características. O número de
independência (G) é a cardinalidade do subconjunto independente
máximo
de
vértices
do
grafo.
No
nosso
exemplo,
𝛼(G) = 4.
(f)
(g)
Coloração
Suponha, no exemplo anterior, o dos professores, que quiséssemos
saber qual o menor número de horários necessários para ministrar as
provas. Para isto, devemos resolver o problema de particionar o conjunto
de vértices do grafo em subconjuntos independentes; cada conjunto
corresponder a um horário de prova. Uma forma de resolver o problema
é atribuir cores aos vértices de forma que vértices adjacentes tenham
necessariamente cores diferentes. O menor número de cores que se pode
utilizar será, portanto a solução do problema.
 Observação: não precisamos efetivamente colorir os vértices, basta
atribuir um número ou um símbolo aos vértices.
Aplicações do conceito de conjunto independente surgem quando,
por exemplo, desejamos evitar duplicação de esforços. Suponhamos que
num parque, representado pelo grafo da figura (e), eu quisesse instalar
barracas para venda de sorvete. A operadora das barracas faz as seguintes
restrições:

Uma barraca deve ser localizada em uma esquina (vértice).

Esquinas próximas (vértices adjacentes) só admitem uma barraca.
O estudo de coloração de grafos nasceu quando Francis Guthrie
percebeu que era possível colorir o mapa da Inglaterra usando apenas 4
cores. A pergunta que surgiu foi se 4 cores eram suficientes para colorir
qualquer decomposição do plano em regiões. Em 1976, usando grafos,
Haken e Appel mostram que a resposta era afirmativa.
Uma coloração de interesse é aquela em que se utiliza um número
mínimo de cores. Um grafo G, que exige k cores para pintar seus vértices,
e não menos, é chamado um grafo k-cromático, ou k-colorável, e o
número k é chamado número cromático de G. Na figura abaixo (i), o
número mínimo de cores é 3, portanto o grafo é 3-cromático.
a
b
Estamos procurando então um conjunto independente. Para instalar o
máximo de barracas procuramos um conjunto independente máximo. Já
vimos que esta pode ser uma tarefa complexa. Na figura abaixo a
configuração da esquerda (f) mostra um conjunto independente maximal,
isto é, não podemos acrescentar mais barracas de sorvete. Mas a
configuração da direita (g) também é independente e contém quase o
dobro de barracas.
a
d
b
b
c
c
(h)
(i)
C o m p l e x o d e E n s i n o S u p e r i o r d e C a c h o e i r i n h a
Rua Silvério Manoel da Silva, 160 - CEP 94930000 - Cachoeirinha – RS - Tel/Fax. (51) 34418650 – www.cesuca.com.br – [email protected]
Recredenciamento
Portaria MEC 347, de 05.04.2012 - D.O.U. 10.04.2012.
Do ponto de vista matemático, o subconjunto de vértices com uma
mesma cor é considerado uma partição de vértices, e no caso do exemplo
(h): {a}, {b, d} e {c}.
Temos então, por definição:
Passo 3 - Repita o Passo 2 com a
segunda cor C2 e os vértices
subsequentes não coloridos.

Uma coloração própria dos vértices de um grafo é uma coloração
de vértices tal que aos vértices (pontos finais) de cada aresta são atribuídas
cores diferentes.
Passo 4 - Repita o Passo 3 com a
terceira cor C3, depois com a quarta
cor C4, e assim por diante, até que
todos os vértices estejam coloridos.

Um
grafo
é
dito
ser
k-cromático ou k-colorável se ele tem uma coloração própria de vértices
que usa k cores.
Vamos ver um exemplo abaixo:

O número cromático de um grafo G, denotado crom(G), é o menor
número de cores diferentes necessárias para obter uma coloração própria
de G.
Teorema das Quatro Cores
A história do problema das quatro cores começou em 1852, quando
Francis Guthrie, aluno de Augustus de Morgan, tentava colorir o mapa
da Inglaterra com cores diferentes de maneiras que não houvesse regiões
vizinhas com a mesma cor. Observou que apenas quatro cores seriam
suficientes, e apresentou o problema a De Morgan. Surgindo então o
Problema das Quatro Cores. Este Teorema foi provado inicialmente em
1976, por Kenneth Appel e Wolfgang Haken na Universidade de Illinois,
com o auxílio de um computador.
O Teorema das Quatro Cores afirma que: Qualquer grafo planar
pode ser colorido com apenas quatro cores.
1º passo: vértice 5 (grau 4) – vértices 1,2,3 e 4 (grau 3)
2º passo: cor azul no vértice 5 (como o restante dos vértices são todos
adjacentes, passamos para próximo passo).
3º passo: cor amarela no vértice 1 e depois no vértice 3, que não é
adjacente ao vértice 1.
4º passo: cor vermelha no vértice 2 e depois cor vermelha no vértice
4, eu não é adjacente ao vértice 2.
Assim o grafo é 3-cromático.
(i) Um grafo é dito planar se pode ser representado no plano sem que
suas linhas se cruzem.
(ii) Um grafo é planar se seu esquema puder ser traçado em um plano de
forma que duas arestas quaisquer se toquem, no máximo, em alguma
extremidade.
Aplicações de Coloração
As aplicações de coloração aparecem quando precisamos repartir o
conjunto de vértices em conjuntos de vértices independentes disjuntos.
Voltando ao problema do parque, suponha que quiséssemos instalar
barracas de sorvete, pipocas, cachorro-quente, algodão doce, etc. Um
algoritmo interessante pode nos ajudar a colorir um grafo.
Algoritmo de Welch-Powell
O Algoritmo de Welch-Powell, é um algoritmo para a coloração de
um grafo G, que consiste em:
Passo 1 - Ordene os vértices de G em ordem decrescente de grau.
Passo 2 - Atribua a primeira cor, C1, ao primeiro vértice e, então,
sequencialmente, atribua C1 a cada vértice que não é adjacente a algum
vértice que o antecedeu e ao qual foi atribuída a cor C1.
C o m p l e x o d e E n s i n o S u p e r i o r d e C a c h o e i r i n h a
Rua Silvério Manoel da Silva, 160 - CEP 94930000 - Cachoeirinha – RS - Tel/Fax. (51) 34418650 – www.cesuca.com.br – [email protected]
Recredenciamento
Portaria MEC 347, de 05.04.2012 - D.O.U. 10.04.2012.
Exercícios II
1) Dê a coloração dos grafos por meio do algoritmo de Welch-Powell e
determine o número cromático (use cores na sequência: azul, amarelo,
vermelho, verde, preto e branco. Também é possível atribuir letras às
cores: a = azul, b = amarelo, c = vermelho, ...).
C o m p l e x o d e E n s i n o S u p e r i o r d e C a c h o e i r i n h a
Rua Silvério Manoel da Silva, 160 - CEP 94930000 - Cachoeirinha – RS - Tel/Fax. (51) 34418650 – www.cesuca.com.br – [email protected]