Trabalho Grupo 8 - Métodos Matemáticos

Equação das Ondas
Muitos fenômenos físicos, aparentemente distintos, podem ser descritos
matematicamente em termos de ondas.
O aspecto essencial da propagação de uma é que esta consiste numa
perturbação auto-sustentada do meio através do qual se propaga.
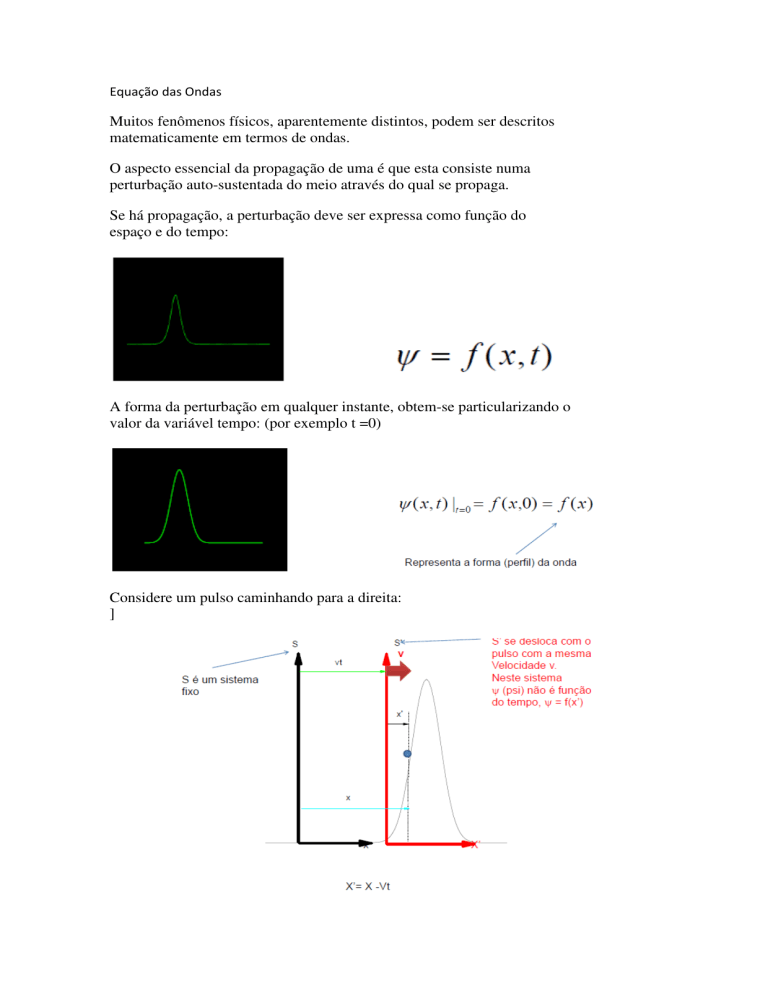
Se há propagação, a perturbação deve ser expressa como função do
espaço e do tempo:
A forma da perturbação em qualquer instante, obtem-se particularizando o
valor da variável tempo: (por exemplo t =0)
Considere um pulso caminhando para a direita:
]
Com base na figura anterior, temos:
Esta equação representa a forma mais geral da função de onda em
uma dimensão.
Basta apenas escolher a forma f(x,o) =f(x) e substituir x por (x-vt) em
f(x)!
Do mesmo modo, se a onda se desloca para a esquerda:
Isto permite obter a forma geral da equação de ondas a uma dimensão:
Se x se mantiver constante, a derivada parcial de (x,t) no tempo é:
Combinando ambas as equações:
Mas como são necessárias duas constantes para especificar totalmente uma
onda , a equação mais geral deve ser de segunda ordem. Calculando as
segundas derivadas parciais:
Uma vez que
E lembrando que
Então
Combinando estas equações, obtemos:
A equação de Ondas!
Que admite soluções da forma
ONDAS PLANAS:
Constituem aos mais simples exemplos de ondas tridimensionais.
Para ondas planas, as superfícies de igual fase são planos, em geral
perpendiculares à direção de propagação da perturbação:
A forma mais reduzida da equação do plano perpendincular à k é
É possível construir um conjunto de planos para os quais (r) dependa
senoidalmente das variáveis espaciais:
A natureza periódica das funções harmônicas no espaço pode ser expressa na
forma:
Para que os planos de igual fase se propaguem é necessário que (r) varie no
tempo, o que se consegue introduzindo a dependência temporal :
Uma onda plana harmônica é representada em coordenadas cartesianas, na forma:
Onde α,β, e γ são os co-senos diretores de k
ONDAS ESFÉRICAS:
O laplaciano em coordenadas esféricas:
Procura-se construir uma descrição de ondas esféricas, ou seja,
Onda esférica harmônica:
ONDAS CILÍNDRICAS:
O Laplaciano em coordenadas cilindricas é
A simetria cilíndrica traduz-se pela seguinte exigência:
Qual deve ser a forma de (r) das soluções desta equação ?
Esta equação representa um conjunto de cilindros coaxiais que preenchem
todo o espaço e que se afastam ou se aproximam de um fonte linear de
comprimento infinito situada no eixo.
Cálculo do Laplaciano em coordenadas esféricas:
Vamos usar os símbolos (r, ɵ, φ) para indicar as coordenadas esféricas de um ponto.
em termos das coordenadas esféricas (r, ɵ, φ). Um cálculo direto é bastante longo. Por
isto segui outro caminho. Usando a expressão do laplaciano em duas variáveis em
termos das coordenadas polares, temos
Notemos que as relações:
são análogas às relações entre as coordenadas cartesianas e polares no plano, somente,
agora, com z e ρ desempenhando, respectivamente, os papéis de x e y. Portanto, usando
novamente a expressão do laplaciano em cordenadas polares, podemos escrever
Somando uzz a ambos os lados em (1), temos
,e usando (2),
Precisamos expressar up em coordenadas esféricas. Pela regra da cadeia,
Em (1), estávamos mantendo z fixo e tomando φ e ρ como variáveis independentes, de
modo que φp= 0 . Portanto,
De
segue que
Por outro lado, de
segue que
Usando (5) e (6) em (7), obtemos
Substituindo (5) e (6) em (4), obtemos
E, portanto,
finalmente, substituindo (9) em (3), obtemos
que é a expressão do laplaciano em coordenadas esféricas.
Solução da Equação da Onda em Coordenadas Esféricas
∇ =
=0
, , , = 0
= ∇ −
1 1 1
1
+
+
= ∇ −
1 1
1
1 1 +
+
−
=0
Usando o método da separação de variáveis:
= 2 + + − =0
1
1
1 1 + 2 ! + + " ! + 1 −
=0
Dividindo a expressão acima por PTR, temos:
1 `` + 2`
1 ` + "%`
1 ``
1 ``
!
+
$
+
&
−
=
1 `` + 2
1 ` + "%`
1 ``
1 ``
!
+
$
+
&
=
= '(
1 ``
= '
⟶
`` = ' `` − ' = 0
⟶
* − ' = 0
⟶
* = ± √' Como esperamos que a solução varie harmonicamente com o tempo, fazemos:
-
'( = − . 3
= /012
⟶
* = ± .4
→
6 = .
1 `` + 2`
1 `` + "%`
1 ``
!+ $
+
& = − .
`` + 2` + . `` + "%`
1 ``
!+ $
+
&=0
x r
`` + 2` + . `` + "%`
1 ``
!= − $
+
& = '
`` + 2`
+ . = '
−$
−
`` + "%`
1 ``
+
& = '
`` "%` ``
+
! − ' = 0
x sen ϕ
x −1
`` + "%` ``
+
+ ' = 0
`` + "%`
``
−
+ ' ! =
= '=
``
= '=
→
`` − '= = 0
∝ + '= = 0
Como P(
é periódica de período 2π,
−
→
∝ = ± ?− '=
'= = − /0@A
`` + "%`
+ ' ! = − `` + "%` + ' − = 0
`` + "%` + ' −
! = 0
Fazendo a mudança de variável = cos , temos:
÷ sen ϕ
C
=
= −
= −
$ & = − −
"
=
−
"
= "
→
?1 − = Substituindo em (I):
− "
− "%
+ ' −
! = 0
1 − −
−
+
'
−
! =0
1 − 1 − −
2
+
'
−
! = 0
1 − CC
Sob esta forma esta equação lembra a equação de Legendre. Para explorar esta
semelhança, faremos uma segunda mudança de variável.
= 1 − @/ 6
@
6 = 1 − @/
+ 1 − / ( −26
2
@
@ 6
1 − = 1 − −
6
1 − = 1 − @/ 6
@ 6
@
6
/ ( −2
1
1
=
−
+
−
2
@
@
@
6
/ (
/ (
/ −2
1
1
−
+
1
−
6
+
H
−
1I
−
−G
6J
2
6 1 − @/ 6 1 − @/ 6 1 − @/ 6
@/
=
1
−
−
−
−
1 − 1 − 1 − 1 − @/
+ 2 K − 1L
6
1 − 2
6
2 6
2 @/
=
1
−
−
−
6
+
6
−
6!
1 − 1 − 1 − 1 − 6
2 6
2 @/
=
1
−
−
+
6
+
−
M−
N!
1 − 1 − 1 − 1 − 6
2 6
− 1 − − 2 @/
=
1
−
−
+
6
M
N !
1 − 1 − 6
2 6
− 1 − @/
= 1 − −
+ 6
!
1 − 1 − 6
2 6
1 − − 1
@/
= 1 − −
− 6!
1 − 1 − Substituindo em (II):
@
1 − O(
@
1 − 6
6 P1 − − 1Q6
6
2 −
2
−
−
2
+
6
+
⋋
−
!6 = 0
1 − 1 − 1 − @
1 − 1 − 6 P1 − − 1Q
6
@/
−
21
−
−
1 − @/ 6 − 21 − @/
1 − 2 1 − @/
+
+ ' −
! 1 − @/ 6 = 0
1 − 1 − P1 − − 1Q
6
6
2 2
−
+
2
+
6
−
+⋋
−
!=0
1 − 1 − 1 − 6
6
2 − P1 − − 1Q + ⋋ 1 − − −
2
+
1
+
6
!=0
1 − 1 − 1 − 6
2 − 1 − + +⋋ 1 − − 6
−
2
+
1
+
6
!=0
1 − 6
6
2 − + − − +⋋ 1 − − −
2
+
1
+
6
!=0
1 − 1 − 6
6
− + − +⋋ 1 − −
2
+
1
+
6
!=0
1 − 1 − 6
⋋ 1 − − 1 − + − 6
−
2
+
1
+
6
!=0
1 − 1 − 1 − 6
⋋ 1 − − + 11 − 6
−
2
+
1
+
6
!=0
1 − 6
6
−
2
+
1
+ 6S⋋ − + 1T = 0
Portanto se fizermos ⋋ = UU + 1 esta equação será satisfeita pelos V
@
derivada de V.
VX = @ V@ "
⋋ = UU + 1 → voltando para a equação em R
²′′ + 2′
+ .²² = UU + 1
′′ + 2 ′ + P. − UU + 1Q = 0
+
2
+ P. − UU + 1Q = 0
Fazendo x = mr e R(r) ⟶ Y(x)
c
c S − UU + 1Tc = 0
+
2
. .
d =
e
√
d = e /(/
²
c
c S − UU + 1Tc = 0
+ 2
CCC
n-ésima
c
e
1
= /(/
+ e − /=/
2
c
1 e e
=
−
√ 2√ =
( 1 e
1 e
3
c
/ e
=
−
−
+
e
2√ = 2√ = 4√ =
1 ²e
1 e
3
c
=
−
+
e
√ ² √ = 4√ =
Substituindo na equação (III):
1 e
1 e
3
1 e e
e
−
+
e! + 2
−
! + S − UU + 1T
=0
=
=
=
√ 4√
√ √ 2√
√
e
2
e
3 e
+
−
!
+
−
+ − UU + 1!
=0
4 √ = √ =
√ √ √ = √
2
e
3 1
1
UU + 1
e
+
−
!
+
−
+
−
! e = 0
4 √ √ √
√ √ = √
√ e
e
3
1
UU + 1
+
+
−
+
−
! e = 0
4√ √ √
√ √ √
e 1 e
1
UU + 1
+
+
−
+
1
−
!e = 0
4
U + U
e 1 e
1
+
+
1
−
−
!e = 0
4 e 1 e
4U + 4U + 1
+
+ 1−
!e = 0
4 1
U + U + 4
e 1 e
+
+ h1 −
ie = 0
1 HU
+
I
e 1 e
2 ke = 0
+
+
j1
−
Comparando com a equação de Bessel modificada:
l 2m + 1 l
m − * n * o +
+
+ /p ! l = 0
l l l
2m + 1 = 1 → m = 0
1 m − * n = − U + →
2
1 1
−n = − U + → n = ± U + 2
2
* o = 1 →
o² = 1
→
o = ±1
Como l é inteiro e p ≠ inteiro, a solução é do tipo:
e = - rVO( + rV/( s
d =
e
√
d = t(
rVO( √
+ t
1
uV = v
r (
w VO
V = v
√
→ rVO( = √w uV 1
x ( →
w VO
xVO( ≈ r/V/( r/V/( r/V/( = y√w V d = t(
rV √w
√
+ t y
d = yV uV + {V V xV √w
√
= .
= yV uV . + {V V .
∅, , , = ∅
∅, , , = y( @ −
y
{( @X + { }@X Pt( cos + t Qy@ 6 + {@ cos6
@O(
Conclusão
A equação de onda é uma importante equação diferencial parcial lineal de segunda
ordem que descreve a propagação de uma variedade de ondas, como as ondas sonoras,
as ondas de luz e as ondas na água. É importante em vários campos como a acústica, o
eletromagnetismo e a dinâmica de fluídos.
Agradecimentos
Agradecemos, primeiramente, ao professor Altair, pela iniciativa de nos propor
esse trabalho visando não só nos preparar para a vida profissional, como ajudar ao
próximo. Aos nossos colegas de turma, em especial os que compartilharam essa tarefa
conosco. Aos nossos pais e familiares, pelo apoio de hoje e sempre.
Referências
- Material disponibilizado na xerox (Prof. Altair)
- Eugene Butkov, Fisica Matemática, 1978 editora Guanabara 2 S.A