EXS PARA PR3 II BIM

Professor:
EXS PARA PR3 II BIM
SÉRIE: 2º ANO
FÍSICA
Conteúdo:
 1a Lei de Ohm (Resistores),
 Associação de Resistores (série, paralelo e mista)
 Potência elétrica e Energia elétrica
1. (Uemg 2016) “Em casa, corria ao banho, à sala, à cozinha
(...). Corria contra a corda bamba, invisível e opressora do
tempo. Era preciso avançar sempre e sempre.”
EVARISTO, 2014, p. 66.
O chuveiro da casa de Cida tem uma potência de 4300 W, na
posição inverno. Como estava quente, Cida mudou a posição
do chuveiro para a posição verão, alterando a resistência
elétrica e a potência do chuveiro.
Ao fazer isso, o chuveiro de Cida:
a) Teve a resistência aumentada e a corrente diminuída.
b) Teve a resistência aumentada e a corrente também
aumentada.
c) Teve a resistência diminuída e a corrente aumentada.
d) Teve a resistência diminuída e a corrente também
diminuída.
2. (G1 - cftrj 2016) Células fotoelétricas ou fotovoltaicas são
dispositivos capazes de transformar a energia luminosa,
proveniente do Sol ou de outra fonte de luz, em energia
elétrica. O conjunto de células fotoelétricas é chamado Placa
Fotovoltaica, e o uso hoje é bastante comum em lugares
afastados da rede elétrica convencional. Existem placas de
várias potências e diferentes tensões para os mais diversos
usos.
Uma placa fotovoltaica com 72,0 W de potência de pico, por
exemplo, é capaz de prover uma diferença de potencial de
12,0 V. Qual a corrente elétrica gerada por esta placa?
a) 864 A.
b) 90,0 A.
c) 12,0 A. d) 6,0 A.
3. (Pucpr 2015) Para fazer o aquecimento de uma sala durante
o inverno, uma família utiliza um aquecedor elétrico ligado à
rede de 120 V. A resistência elétrica de operação apresentada
por esse aquecedor é de 14,4 Ω. Se essa família utilizar o
aquecedor diariamente, por três horas, qual será o custo
mensal cobrado pela companhia de energia se a tarifa for de
R$ 0,25 por kW  h?
Considere o mês de 30 dias.
ELTON PITA
DATA: 28 / 06 / 2016
a) R$ 15,00. b) R$ 22,50. c) R$ 18,30.
d) R$ 52,40. e) R$ 62,80.
4. (Imed 2015) Considere uma bateria ideal de 12 V, na qual
é ligada uma lâmpada. Logo após ser ligada, a lâmpada atinge
um brilho que não varia ao longo do tempo. Nesse estado, a
corrente elétrica que percorre a lâmpada é igual a 0,5 A.
Desprezando efeitos de dissipação nos fios condutores,
determine, respectivamente, a resistência elétrica da lâmpada e
a potência dissipada por ela.
a) 32 Ohms e 12 Watts.
b) 12 Ohms e 12 Watts.
c) 24 Ohms e 6 Watts.
d) 24 Ohms e 12 Watts.
e) 32 Ohms e 24 Watts.
5. (Pucrj 2015) Uma lâmpada é ligada a uma bateria de
120 V e dissipa 40,0 W. A resistência dessa lâmpada, em
Ω, é:
a) 8,00  102
c) 3,00
e) 360
b) 0,33
d) 80,0
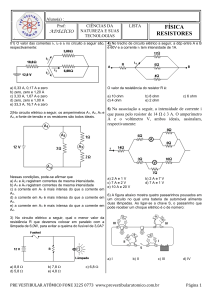
6. (G1 - ifsul 2015) Quatro resistores, todos de mesma
Resistência Elétrica R, são associados entre os pontos A e B
de um circuito elétrico, conforme a configuração indicada na
figura.
A resistência elétrica equivalente entre os pontos A e B é
igual a
R
3R
4R
a)
b)
c)
d) 4R
4
4
3
7. (Mackenzie 2014) No circuito desenhado abaixo, a
intensidade de corrente elétrica contínua que passa pelo
resistor de 50 Ω é de 80 mA.
resistores em série, em função da intensidade de corrente
elétrica que atravessa a associação de resistência equivalente
RS, e a curva P representa a variação da diferença de potencial
elétrico entre os extremos da associação dos dois resistores em
paralelo, em função da intensidade da corrente elétrica que
atravessa a associação de resistência equivalente RP.
A força eletromotriz ε do gerador ideal é igual a
a) 1,5 V
b) 3,0 V
c) 4,5 V
d) 5,0 V
e) 6,0 V
8. (G1 - col.naval 2014) Considere que um determinado
estudante, utilizando resistores disponíveis no laboratório de
sua escola, montou os circuitos apresentados abaixo:
Considere a associação seguinte, constituída por dois
resistores R1 e dois resistores R2.
Querendo fazer algumas medidas elétricas, usou um
voltímetro (V) para medir a tensão e um amperímetro (A) para
medir a intensidade da corrente elétrica. Considerando todos
os elementos envolvidos como sendo ideais, os valores
medidos pelo voltímetro (situação 1) e pelo amperímetro
(situação 2) foram, respectivamente:
a) 2V e 1,2A
b) 4V e 1,2A
c) 2V e 2,4A
d) 4V e 2,4A
e) 6V e 1,2A
9. (G1 - utfpr 2014) Num dia frio, certo chuveiro elétrico é
ligado para dissipar uma potência de 7200 W. Se o tempo em
que permanece ligado é de dez minutos, a energia elétrica que
consome, em kWh, é de:
a) 1,5. b) 1,8. c) 2,2. d) 3,0. e) 1,2.
De acordo com as informações e desprezando a resistência
elétrica dos fios de ligação, calcule a resistência equivalente da
associação representada na figura e os valores de R1 e R2,
ambos em ohms.
13. (Pucrj 2013) O gráfico abaixo apresenta a medida da
variação de potencial em função da corrente que passa em um
circuito elétrico.
10. (Uerj 2014) Um chuveiro elétrico com resistência igual a
5Ω é conectado a uma rede elétrica que fornece 120 V de
tensão eficaz.
Determine a energia elétrica, em kWh, consumida pelo
chuveiro durante 10 minutos.
11. (G1 - cftmg 2014) Em uma residência com 4 pessoas,
cada uma delas utiliza diariamente um chuveiro de 4800 W
ligado por 10 min durante o banho. Além disso, essa casa é
iluminada por 10 lâmpadas fluorescentes de 20 W cada. Para
que o consumo de energia dessas lâmpadas seja o mesmo do
chuveiro em 30 dias, elas devem ficar ligadas continuamente
durante
a) 2 dias. b) 5 dias. c) 15 dias. d) 20 dias.
12. (Unesp 2014) Dois resistores ôhmicos, R1 e R2, podem ser
associados em série ou em paralelo. A resistência equivalente
quando são associados em série é RS e quando são associados
em paralelo é RP.
No gráfico, a curva S representa a variação da diferença de
potencial elétrico entre os extremos da associação dos dois
Podemos dizer que a resistência elétrica deste circuito é de:
a) 2,0 m b) 0,2  c) 0,5  d) 2,0 k e) 0,5 k
TEXTO PARA A PRÓXIMA QUESTÃO:
Leia o texto:
No anúncio promocional de um ferro de passar roupas a vapor,
é explicado que, em funcionamento, o aparelho borrifa
constantemente 20 g de vapor de água a cada minuto, o que
torna mais fácil o ato de passar roupas. Além dessa explicação,
o anúncio informa que a potência do aparelho é de 1 440 W e
que sua tensão de funcionamento é de 110 V.
2
14. (Fatec 2013) Jorge comprou um desses ferros e, para
utilizá-lo, precisa comprar também uma extensão de fio que
conecte o aparelho a uma única tomada de 110 V disponível
no cômodo em que passa roupas. As cinco extensões que
encontra à venda suportam as intensidades de correntes
máximas de 5 A, 10 A, 15 A, 20 A e 25 A, e seus preços
aumentam proporcionalmente às respectivas intensidades.
Sendo assim, a opção que permite o funcionamento adequado
de seu ferro de passar, em potência máxima, sem danificar a
extensão de fio e que seja a de menor custo para Jorge, será a
que suporta o máximo de
a) 5 A. b) 10 A. c) 15 A. d) 20 A. e) 25 A.
15. (G1 - cftmg 2012) A figura representa um trecho de um
circuito elétrico em que a diferença de potencial entre os
pontos A e B vale 12 V.
E  energia elétrica em joules (J) no Sistema Internacional
(SI), porém para o problema é conveniente usar a unidade
usual kWh;
P  potência elétrica em watts no SI. Usaremos em kW;
Δt  tempo em segundos (s) no SI. Usaremos em horas (h).
Primeiramente, calculamos a Potência Elétrica com a equação:
P  U  i, em que:
U  diferença de potencial elétrico em volts (V);
i  intensidade da corrente elétrica em ampères (A).
Como não dispomos do valor da intensidade da corrente
elétrica (i), usamos a 1ª Lei de Ohm para substituí-la por uma
relação entre diferença de potencial e resistência.
U
U  R i  i 
R
Substituindo na equação da potência, temos:
P
U2
, onde R  resistência elétrica em ohms (Ω)
R
Logo, P 
A
O valor da intensidade de corrente elétrica i, em ampères, e da
resistência elétrica do resistor R, em ohm, valem,
respectivamente,
a) 2,0 e 6,0.
b) 4,0 e 2,0.
c) 6,0 e 2,0.
d) 6,0 e 4,0.
120 V 2
14,4 Ω
Energia
Resposta da questão 2: [D]
A potência elétrica em função da corrente é dada por: P  U  i
Onde,
P : a potência em watt
U : a diferença de potencial em volt
i : a intensidade da corrente elétrica em ampères
Assim,
P
72 W
i i
i  6 A
U
12 V
Elétrica
em
kWh
será:
Como o custo mensal da Energia Elétrica consumida é apenas
o produto da Energia Elétrica em kWh pelo seu valor, temos:
R$0,25
 R$ 22,50
kWh
Resposta da questão 4: [C]
A resolução desta questão é aplicação de fórmula direta.
Sabendo que a tensão aplicada à lâmpada é U  12 V, e a
corrente que está circulando no circuito é i  0,5 A, pode-se
aplicar a 1ª Lei de Ohm de forma a encontrar o valor da
resistência.
U  R i
U 12
R 
i 0,5
R  24 Ω
Gabarito:
Resposta da questão 1: [A]
De acordo com a Primeira Lei de Ohm, resistência elétrica e
intensidade da corrente são inversamente proporcionais,
portanto ao diminuir a potência elétrica, deve-se diminuir a
corrente e aumentar a resistência.
14400 V 2
 1000 W  1 kW
14,4 Ω
3h
E  P  Δt  1 kW 
 30 dias  90 kWh
dia
Custo  90kWh 
16. (Ufsm 2012) O uso de datashow em sala de aula é muito
comum. As lâmpadas de filamento que são usadas nesses
equipamentos têm potência elevada de, aproximadamente,
1100 W quando ligadas em 220 V. Se um datashow for usado
durante 1 hora e 40 minutos, que é o tempo de duração de uma
aula com dois períodos, qual é a energia consumida em J?
a) 5,00 X 102.
b) 2,42 X 103.
5
c) 1,10 X 10 .
d) 6,60 X 106.
8
e) 1,45 X 10 .

E para a potência,
P  i U
P  0,5  12
P6W
Resposta da questão 5: [E]
A potência elétrica em função da diferença de potencial e da
resistência elétrica é obtida pela equação:
P
U2
R
Sendo assim, basta substituir os valores e calcular a resistência
elétrica.
U2 120 V 

 360 Ω
P
40 W
2
R
Resposta da questão 6: [C]
Resposta da questão 3: [B]
A Energia Elétrica é dada por: E  P  Δt, onde:
Req 
3
R
R 
3
Req 
4R
.
3
Calculando a resistência equivalente:
Resposta da questão 7: [E]
As resistências estão associadas em série, portanto a
resistência equivalente é:
Req  50 Ω  25 Ω  75 Ω
Com a primeira lei de Ohm, obtemos a tensão elétrica.
U  R i
U  75Ω  80  103 A  U  6 V
Req  RS  RP  16  3 
Resposta da questão 8: [B]
Situação I
Como os resistores estão em série, a resistência equivalente é
igual à soma das resistências. O valor medido pelo voltímetro
é a ddp no resistor de 40.
Aplicando a lei de Ohm-Pouillet:
ε  Re q i  12   60  40  20  i  i 
U  R i  40  0,1 
12
 i  0,1 A.
120
- Valores de R1 e R2.
Do item anterior:
RS  16  R1  R2  16 (I)

R1 R2

 3 (II)
RP  3 
R1  R2

Situação II
Calculando a resistência equivalente:
16  8

R1  2

R  16  8
 1
2
 Req  10 Ω.
O valor medido pelo amperímetro é a corrente total no
circuito.
Aplicando a lei de Ohm-Pouillet:
ε
12
ε  Req i  i 

 i  1,2 A.
Req 10
Resposta da questão 9: [E]
Dados: P = 7.200 W = 7,2 kW; Δt  10min  1/ 6h.
1
6

E  1,2 kWh.
Resposta da questão 10:
Dados: R  5Ω; U  120 V; Δ t  10min  1/ 6h.
ΔE  P Δt 
U2
1202 1
Δt 
  480 W  h  ΔE  0,48 kW  h.
R
5
6
Resposta da questão 11: [D]
A energia consumida deve ser a mesma nos dois casos:
E1  E2
 4 P1 Δ t1  10 P2 Δ t 2
28.800
Δt 2  28.800 min  Δt 2 
24  60
 4  4.800  10  30  10  20 Δt 2
R1 R2
 3  R1 R2  48. (III)
16
R1  R2  16  R2  16  R1 (I)
(I) em (III)  R1 16  R1   48 
R R  48 (III)
 1 2
R12  16 R1  48  0  R1 
E  P  7,2 
(I) em (II) 
Rearranjando:
U  4 V.
1
1
1
1 1 2  3
6
1






Req 60 30 20
60
60 10
Req  19 Ω


Δt 2  20 dias.
Resposta da questão 12:
- Resistência equivalente (Req) da associação representada.
Da leitura direta do gráfico:
16  162  4 1 48 
2

16  8
2

 R1  12 Ω  R2  16  12  R 2  4 Ω
 R1  4 Ω  R2  16  4  R 2  12 Ω.
Portanto, um dos resistores tem resistência 4 Ω e,o outro,
12 Ω.
Resposta da questão 13: [D]
Primeira Lei de OHM
V  R.i  12  Rx6  R  2,0k
Resposta da questão 14: [C]
Dados: P = 1.440 W; U = 110 V.
Da expressão da potência elétrica:
P 1.440
PU i  i 
 13,1 A.
U
110
Portanto, de acordo com as opções fornecidas, a extensão
adequada é a que suporta o máximo de 15 A.
Resposta da questão 15: [D]
Como os dois resistores estão em paralelo, a ddp, U = 12 V, é
a mesma nos dois ramos. Aplicando a 1ª lei de Ohm:
12  2 i  i  6 A.
UR i 
12  R 3  R  4 Ω.
Resposta da questão 16: [D]
Dados: P = 1.100 W; t = 1 h e 40 min = 6.000 s.
E  P t  1.100  6.000   6,6  106 J.
U 48
i  3 A
Série 
 U  RS i  RS  
 RS  16 Ω.
i
3
U  48 V
U 9
i  3 A
Paralelo 
 U  RP i  RP  
 RP  3 Ω.
i 3
U  9 V
4