Física 4 – T.D. Nº 02

Natureza:
Física 4 – T.D. Nº 02
Aluno(a):
Professor(a): Augusto Melo
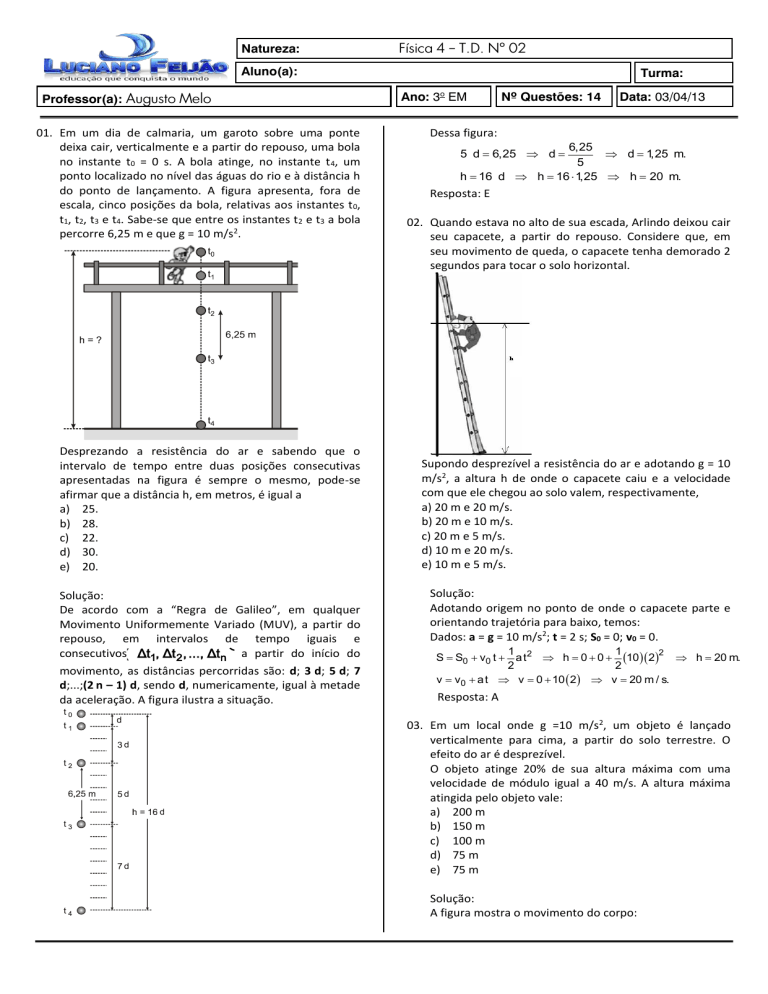
01. Em um dia de calmaria, um garoto sobre uma ponte
deixa cair, verticalmente e a partir do repouso, uma bola
no instante t0 = 0 s. A bola atinge, no instante t 4, um
ponto localizado no nível das águas do rio e à distância h
do ponto de lançamento. A figura apresenta, fora de
escala, cinco posições da bola, relativas aos instantes t 0,
t1, t2, t3 e t4. Sabe-se que entre os instantes t2 e t3 a bola
percorre 6,25 m e que g = 10 m/s2.
Desprezando a resistência do ar e sabendo que o
intervalo de tempo entre duas posições consecutivas
apresentadas na figura é sempre o mesmo, pode-se
afirmar que a distância h, em metros, é igual a
a) 25.
b) 28.
c) 22.
d) 30.
e) 20.
Solução:
De acordo com a “Regra de Galileo”, em qualquer
Movimento Uniformemente Variado (MUV), a partir do
repouso, em intervalos de tempo iguais e
consecutivos( Δt1, Δt 2 , ..., Δtn )a partir do início do
movimento, as distâncias percorridas são: d; 3 d; 5 d; 7
d;...;(2 n – 1) d, sendo d, numericamente, igual à metade
da aceleração. A figura ilustra a situação.
Turma:
Ano: 3o EM
Nº Questões: 14
Data: 03/04/13
Dessa figura:
6,25
 d  1,25 m.
5
h  16 d  h  16  1,25  h  20 m.
5 d  6,25  d 
Resposta: E
02. Quando estava no alto de sua escada, Arlindo deixou cair
seu capacete, a partir do repouso. Considere que, em
seu movimento de queda, o capacete tenha demorado 2
segundos para tocar o solo horizontal.
Supondo desprezível a resistência do ar e adotando g = 10
m/s2, a altura h de onde o capacete caiu e a velocidade
com que ele chegou ao solo valem, respectivamente,
a) 20 m e 20 m/s.
b) 20 m e 10 m/s.
c) 20 m e 5 m/s.
d) 10 m e 20 m/s.
e) 10 m e 5 m/s.
Solução:
Adotando origem no ponto de onde o capacete parte e
orientando trajetória para baixo, temos:
Dados: a = g = 10 m/s2; t = 2 s; S0 = 0; v0 = 0.
1
1
2
S  S0  v0 t  at 2  h  0  0  10  2  h  20 m.
2
2
v  v0  at  v  0  10  2  v  20 m / s.
Resposta: A
03. Em um local onde g =10 m/s2, um objeto é lançado
verticalmente para cima, a partir do solo terrestre. O
efeito do ar é desprezível.
O objeto atinge 20% de sua altura máxima com uma
velocidade de módulo igual a 40 m/s. A altura máxima
atingida pelo objeto vale:
a) 200 m
b) 150 m
c) 100 m
d) 75 m
e) 75 m
Solução:
A figura mostra o movimento do corpo:
T.D. de Física – Prof. Augusto Melo
e) velocidade da régua é constante, o que provoca uma
passagem linear de tempo.
Solução:
O peso da régua é constante (P = mg). Desprezando a
resistência do ar, trata-se de uma queda livre, que é um
movimento uniformemente acelerado, com aceleração
de módulo a = g.
A distância percorrida na queda (h) varia com o tempo
conforme a expressão:
1
h  gt 2 .
2
Dessa expressão, conclui-se que a distância percorrida é
diretamente proporcional ao quadrado do tempo de
queda, por isso ela aumenta mais rapidamente que o
tempo de reação.
Resposta: D
Texto
Aplicando Torricelli, vem:
2
V 
V02
2
 2aΔS  0  40  2  10  0,8 H .
Paraquedista
 16 H  1600  H  100 m
Resposta: C
04. Para medir o tempo de reação de uma pessoa, pode-se
realizar a seguinte experiência:
I.
Mantenha uma régua (com cerca de 30 cm)
suspensa
verticalmente,
segurando-a
pela
extremidade superior, de modo que o zero da régua
esteja situado na extremidade inferior.
II.
A pessoa deve colocar os dedos de sua mão, em
forma de pinça, próximos do zero da régua, sem
tocá-la.
III.
Sem aviso prévio, a pessoa que estiver segurando a
régua deve soltá-la. A outra pessoa deve procurar
segurá-la o mais rapidamente possível e observar a
posição onde conseguiu segurar a régua, isto é, a
distância que ela percorre durante a queda.
O quadro seguinte mostra a posição em que três pessoas
conseguiram segurar a régua e os respectivos tempos de
reação.
Distância percorrida pela
Tempo de reação
régua durante a queda (metro)
(segundo)
0,30
0,24
0,15
0,17
0,10
0,14
Ao saltar de um avião a 4 km de altura, um paraquedista tem,
no início, a mesma sensação de frio na barriga que você sente
quando desce a primeira rampa de uma montanha-russa.
Essa impressão se deve à atração gravitacional, que imprime
uma aceleração uniforme ao corpo do paraquedista.
Mas, ao contrário do que se imagina, no salto, o frio na
barriga acaba antes que o paraquedas seja aberto. É que, em
um determinado instante, a força de atração gravitacional é
contrabalançada pela força de resistência do ar, e o corpo
adquire uma velocidade constante de, aproximadamente,
200 km/h. A partir desse momento, o paraquedista não tem
mais sensação de queda, mas, sim, de flutuação. No entanto,
para chegar ao solo com segurança, é preciso reduzir ainda
mais a velocidade. Ao abrir o velame, a resistência ao ar fica
maior e a velocidade cai para cerca de 20 km/h. Toda essa
emoção da queda livre e da flutuação não é privilégio de
quem pratica o paraquedismo como esporte. Esta é também
uma especialidade dos profissionais militares de carreira. Os
paraquedistas do Exército, da Marinha e da Aeronáutica são
oficiais que passam por quatro anos de formação para depois
receber treinamento nessa especialização, que será
empregada em situações de combate e resgate.
Disponível em: http://br.geocities.com. Acesso em: 1 fev.
2009.
A distância percorrida pela régua aumenta mais
rapidamente que o tempo de reação porque a
a) energia mecânica da régua aumenta, o que a faz cair
mais rápido.
b) resistência do ar aumenta, o que faz a régua cair
com menor velocidade.
c) aceleração de queda da régua varia, o que provoca
um movimento acelerado.
d) força peso da régua tem valor constante, o que gera
um movimento acelerado.
Adaptado de: ALVARENGA, Beatriz; MÁXIMO, Antônio. Física.
São Paulo: Scipione. 2004. p. 33.
Imagem disponível em: www.fotosearch.com.br. Acesso em:
04 jul. 2010.
2
T.D. de Física – Prof. Augusto Melo
05. De acordo com o texto, 4 quilômetros é a distância do
chão até a altura do avião. Se um objeto pequeno for
solto dessa altura, quanto tempo em segundos levaria
para chegar ao solo? (Despreze a resistência do ar e
considere a aceleração gravitacional do local de 10 m/s 2).
a)
800 s .
b)
c)
d)
e)
1
1
S  V0 .t  at2  740   3,7t 2  t  20s
2
2
O movimento na horizontal é uniforme:
S  V.t  30  20  600m
Resposta: E
08. O atleta húngaro Krisztian Pars conquistou medalha de
ouro na olimpíada de Londres no lançamento de
martelo. Após girar sobre si próprio, o atleta lança a bola
a 0,50 m acima do solo, com velocidade linear inicial que
forma um ângulo de 45° com a horizontal. A bola toca o
solo após percorrer a distância horizontal de 80 m.
2065 s
2865 s
4443 s
9998 s
Solução:
Dados: h = 4 km = 4.000 m; g = 10 m/s2.
Da equação da queda livre:
2  4.000 
1 2
2h
gt  t 

2
g
10
Resposta: A
h
 t  800 s.
06. Um projétil é lançado com uma velocidade escalar inicial
de 20 m/s com uma inclinação de 30° com a horizontal,
estando inicialmente a uma altura de 5,0 m em relação
ao solo.
A altura máxima que o projétil atinge, em relação ao
solo, medida em metros, é:
Considere a aceleração da gravidade g = 10 m/s2.
a) 5,0
b) 10
c) 15
d) 20
e) 25
Nas condições descritas do movimento parabólico da
bola, considerando a aceleração da gravidade no local
igual a 10 m/s2, 2 igual a 1,4 e desprezando-se as
perdas de energia mecânica durante o voo da bola,
determine, aproximadamente a altura máxima, em
metros, atingida pela bola.
a) 28 m
b) 20,1 m
c) 12 m
d) 8 m
e) 4 m
Solução:
Decompondo a velocidade inicial, teremos uma
componente vertical de V.sen30  20x0,5  10 m/s
A partir da posição inicial, podemos calcular o
deslocamento vertical até o ponto mais alto da
trajetória, utilizando a equação de Torricelli:
Solução:
Dados: A = 80 m; 2 = 1,4; g = 10 m/s2.
A interpretação do problema leva à seguinte ilustração:
V2  V02  2.a.ΔS  0  102  2x10xΔS  ΔS  5,0 m
Como o corpo havia partido de 5,0 m de altura, sua
altura máxima será H: 5 + 5 = 10 m.
Resposta: B
07. Do alto de uma montanha em Marte, na altura de 740 m
em relação ao solo horizontal, é atirada horizontalmente
uma pequena esfera de aço com velocidade de 30 m/s.
Na superfície deste planeta a aceleração gravitacional é
de 3,7 m/s2.
A partir da vertical do ponto de lançamento, a esfera
toca o solo numa distância de, em metros,
a) 100
b) 200
c) 300
d) 450
e) 600
Chamando a direção vertical de y e a horizontal de x,
temos que as componentes horizontais e verticais da
velocidade no momento do lançamento são:
vox  voy  v0 cos 45 
vox  voy  v0
Solução:
O movimento na vertical é uniformemente variado:
2
2
 vox  v oy  0,7v 0
O movimento vertical da bola é um M.U.V., assim as
posições no eixo y são descritas por:
3
T.D. de Física – Prof. Augusto Melo
a
g
S  S0  V0t  t 2  Y  Y0  V0Y t  t 2 (1)
2
2
O movimento na horizontal é uniforme, assim, as posições
no eixo x são descritas por:
S  V  t  X  V0X  t  t 
X
(2)
V0  cos
A velocidade da granada, ao sair do lançador, é de
100 m s e forma um ângulo “α” com a horizontal; a
Substituindo o tempo da equação (2) na equação (1),
ficamos com a equação da trajetória:
aceleração da gravidade é igual a 10 m s2 e todos os
atritos são desprezíveis. Para que a granada atinja o
ponto A, somente após a sua passagem pelo ponto de
maior altura possível de ser atingido por ela, a distância
D deve ser de:
Dados: Cos α  0,6; Sen α  0,8.
a) 240 m
b) 360 m
c) 480 m
d) 600 m
e) 960 m
2

 g

X
X
Y  Y0  V0  sen  
 
 
 V0  cos   2  V0  cos  
g
X2
Y  Y0  tg   X 
2 V 20  cos2 
Considerando o referencial no solo, conforme ilustra a
figura, quando a bola atinge o chão, temos: x = 80 m e y =
0 m, assim:
g
X2
Y  Y0  tg   X 

2 V 20  cos2 
0  0,5  tg 45 80 
Solução:
Decompondo a velocidade em componentes horizontal e
vertical, temos:

Vx  V0 .cos α  100x0,6  60 m/s


Vy  V0 .senα  100x0,8  80 m/s
Na vertical o movimento é uniformemente variado.
Sendo assim:
10
802

2 V 20  cos2 45
802
802
2

80,5

V


0
1
V 20  cos2 45
80,5 
2
64000
V 20 
 V 20  800  V0 28 m / s
80,5
5
1
ΔSy  Vy .t  gt 2  300  80t  5t 2  t 2  16t  60  0
2
A equação acima tem duas soluções: t= 6s e t’=10 s.
Como o projétil já passou pelo ponto mais alto, devemos
considerar o maior tempo (10s).
Na horizontal, o movimento é uniforme. Sendo assim:
ΔSx  Vx .t  D  60x10  600m
Resposta: D
Na altura máxima a velocidade vertical é igual a zero,
assim, para o movimento vertical da bola, a partir do
ponto de lançamento, temos:
V 2  V02  2aS  0  (V0sen45)  2g  H 
2
 2
(28)


2 
V02 sen2 45

H 
 H 

2g
20
H  19,6 m  H  H  H0  19,6  H  0,5 
H  20,1 m
10. Uma noiva, após a celebração do casamento, tinha de
jogar o buquê para as convidadas. Como havia muitas exnamoradas do noivo, ela fazia questão de que sua
melhor amiga o pegasse. Antes de se virar para, de
costas, fazer o arremesso do buquê, a noiva, que possuía
conhecimento sobre movimento balístico, calculou a que
distância aproximada a amiga estava dela: 5,7 m. Então
ela jogou o buquê, tomando o cuidado para que a
direção de lançamento fizesse um ângulo de 60° com a
horizontal. Se o tempo que o buquê levou para atingir a
altura máxima foi de 0,7 s, qual o valor aproximado da
velocidade dele ao sair da mão da noiva? (Despreze o
atrito com o ar. Considere a aceleração da gravidade
2
Resposta: B
09. Um lançador de granadas deve ser posicionado a uma
distância D da linha vertical que passa por um ponto A.
Este ponto está localizado em uma montanha a de
altura em relação à extremidade de saída da granada,
conforme o desenho abaixo.
igual a 10 m s2 , cos60  0,5 e sen60  0,87.)
a) 1,5 m s
b) 5,5 m s
c) 6,0 m s
4
T.D. de Física – Prof. Augusto Melo
Portanto o tempo total é T = 2tq .
O menor tempo de voo da bola é aquele correspondente
à menor altura.
Resposta: B
d) 8,0 m s
e) 11,0 m s
Solução:
Dados: tsub = 0,7 s; A = 5,7 m; g = 10 ms2; θ = 60°.
12. “O importante não é competir e, sim, celebrar.”
Se a amiga apanhou o buquê na mesma horizontal em
Em sua sabedoria milenar, a cultura indígena valoriza
que foi lançado, o tempo total de movimento (tT) foi o
muito o celebrar. Suas festas são manifestações alegres
dobro do tempo de subida (tsub) e o alcance horizontal
de amor à vida e à natureza. Depois de contatos com
(A) foi igual a 5,7 m.
outras culturas, as comunidades indígenas criaram
No lançamento oblíquo, a componente horizontal da
diversos mecanismos políticos, sociais e econômicos. Foi
velocidade de lançamento (v0x) é constante, portanto o
nesse contexto que nasceu a ideia dos Jogos dos Povos
movimento é uniforme. Então:
Indígenas cujo objetivo é unir as comunidades. Todos
ΔS  v Δt  A  v 0x t T  A  v 0 cos60  2t sub  
participam, promovendo a integração entre as diferentes
tribos através de sua cultura e esportes tradicionais.
5,7
 1
5,7  v0    2  0,7   v 0 
 8,14 
0,7
2
(Carlos Justino Terena Disponível em:
v0  8,0 m / s.
http://www.funai.gov.br/indios/jogos/jogos_indigenas.h
tm Acesso em: 29.08.2010. Adaptado)
Resposta: D
Desde outubro de 1996, os Jogos dos Povos Indígenas
são realizados, em diversas modalidades, com a
participação de etnias de todo o Brasil. Uma dessas
modalidades é o arco e flecha em que o atleta tem
direito a três lances contra um peixe desenhado num
alvo, que fica a 30 metros de distância.
Ao preparar o lance, percebe-se que o atleta mira um
pouco acima do alvo. Isso se deve à
a) baixa tecnologia do equipamento, já que não possui
sistema de mira adequado.
b) ação da gravidade que atrai a flecha em direção à
Terra.
c) inadequada percepção do tamanho do alvo, por
conta da distância.
d) rotação da Terra que modifica a trajetória da flecha.
e) baixa energia potencial armazenada pela corda.
11. Após um ataque frustrado do time adversário, o goleiro
se prepara para lançar a bola e armar um contra-ataque.
Para dificultar a recuperação da defesa adversária, a bola
deve chegar aos pés de um atacante no menor tempo
possível. O goleiro vai chutar a bola, imprimindo sempre
a mesma velocidade, e deve controlar apenas o ângulo
de lançamento. A figura mostra as duas trajetórias
possíveis da bola num certo momento da partida.
Assinale a alternativa que expressa se é possível
determinar qual destes dois jogadores receberia a bola
no menor tempo. Despreze o efeito da resistência do ar.
a) Sim, é possível, e o jogador mais próximo receberia a
bola no menor tempo.
b) Sim, é possível, e o jogador mais distante receberia a
bola no menor tempo.
c) Os dois jogadores receberiam a bola em tempos
iguais.
d) Não, pois é necessário conhecer os valores da
velocidade inicial e dos ângulos de lançamento.
e) Não, pois é necessário conhecer o valor da
velocidade inicial.
Solução:
A força peso, atuando sobre a flecha, faz com que sua
trajetória seja desviada para baixo durante o movimento.
Por isso, o atirador tem que lançá-la numa linha de
visada acima do alvo.
Resposta: B
13. Um superatleta de salto em distância realiza o seu salto
procurando atingir o maior alcance possível. Se ele se
lança ao ar com uma velocidade cujo módulo é 10 m/s, e
fazendo um ângulo de 45° em relação a horizontal, é
correto afirmar que o alcance atingido pelo atleta no
salto é de:
(Considere g = 10 m/s2)
a) 2 m.
b) 4 m.
c) 6 m.
d) 8 m.
e) 10 m.
Solução:
No ponto mais alto a componente vertical da velocidade
é nula. A partir daí, e na vertical, temos uma queda livre
a partir do repouso.
O tempo de queda pode ser tirado da expressão
1
H  gt 2 .
2
Sendo assim quanto maior for a altura maior será o
tempo de queda.
Não podemos esquecer que os tempos de subida e
descida são iguais.
Solução:
Dados: v0 = 10 m/s;  = 45°; g = 10 ms/2.
5
T.D. de Física – Prof. Augusto Melo
do solo depois do chute e o ponto onde ela tocou o solo
atrás da linha de fundo era, em metros, um valor mais
próximo de
a) 52,0.
b) 64,5.
c) 76,5.
d) 80,4.
e) 86,6.
v0x = v0 cos 45° = 10
2
 5 2 m/s.
2
Solução:
Dados: v0 = 30 m/s; θ = 30°; sen 30° = 0,50 e cos 30° = 0,85
e t = 3 s.
A componente horizontal da velocidade (v0x) mantém-se
constante. O alcance horizontal (A) é dado por:
A  v0x t  A  v0 cos30 t  A  30 0,85 3  
2
 5 2 m/s
2
No eixo y o movimento é uniformemente variado, com a
= –g.
Calculemos o tempo de subida (tsub), notando que no
ponto mais alto vy = 0.
v0y = v0 sen 45° = 10
A  76,5 m.
Resposta: C
2
s.
2
Como o tempo de subida é igual ao de descida, o tempo
total (tT) é:
vy = voy – g t  0 = 5 2 – 10 tsub  tsub =
tT = 2 tsub =
2 s.
No eixo x o movimento é uniforme, com velocidade igual
a v0x. O alcance horizontal (D) é:
D = v0x tT = 5 2  2  D = 10 m.
Resposta: E
14. O gol que Pelé não fez
Na copa de 1970, na partida entre Brasil e
Tchecoslováquia, Pelé pega a bola um pouco antes do
meio de campo, vê o goleiro tcheco adiantado, e arrisca
um chute que entrou para a história do futebol brasileiro.
No início do lance, a bola parte do solo com velocidade
de 108 km/h (30 m/s), e três segundos depois toca
novamente o solo atrás da linha de fundo, depois de
descrever uma parábola no ar e passar rente à trave,
para alívio do assustado goleiro.
Na figura vemos uma simulação do chute de Pelé.
Considerando que o vetor velocidade inicial da bola após o
chute de Pelé fazia um ângulo de 30° com a horizontal
(sen30° = 0,50 e cos30° = 0,85) e desconsiderando a
resistência do ar e a rotação da bola, pode-se afirmar que
a distância horizontal entre o ponto de onde a bola partiu
6