1 Resoluções dos testes propostos

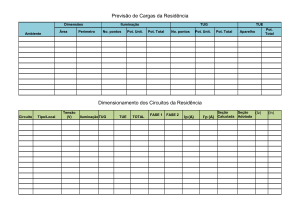
Testes propostos
Capítulo
7
Unidade B
Capítulo 7 Associação de resistores
os fundamentos
da física
T.146
Associação de resistores
3
1
Resoluções dos testes propostos
Resposta: b
220 V � 5 V � 5 V � ... � 5 V ⇒ 220 � n � 5 ⇒ n � 44
1
T.147
2
n
Resposta: b
i
––
4
i
R
U
12 Ω
R
U
i
U = (R + 12) • ––
4
U=R•i
Igualando:
R � i � (R � 12) �
T.148
i
⇒ 4R � R � 12 ⇒ 3R � 12 ⇒
4
R�4Ω
Resposta: c
Situação inicial:
I
R
U�R�I �
U
Os aparelhos ligados ao benjamim são associados em paralelo ao primeiro aparelho.
R
I’
R
––
2
R
––
4
U
1
Req.
�
1
2
4
1
7
R
�
�
⇒
�
⇒ Req. �
R
R
R
Req.
R
7
Unidade B
Capítulo da
7 Associação
de3resistores
Os fundamentos
Física • Volume
• Capítulo 7
3
os fundamentos
da física
22
Testesdos
propostos
Resoluções
testes propostos
Aplicando a lei de Ohm:
U � Req. � I’ ⇒ U �
R
� I’ �
7
Igualando � e �:
R � I’ � R � I ⇒ I’ � 7 � I
7
T.149
Resposta: c
O circuito do aluno desatento é o seguinte:
R
A
C
R
A
C
B
B
R
A
B
R
––
2
R
––
2
R
R
C
R
C
R
A
Curto
R
B
R
––
2
R
––
2
C
R
Portanto: Req. � R ⇒ Req. � 100 Ω
T.150
Resposta: b
2R
A
A
R
2R
B
B
D
2R
R
R
2R
C
E
2R
R
A
R
2R
D
R
2R
E
R
C
B
R
R
R
R
2R
2R
2R
2R
A
R
R
D
E
R
C
R
B
R
A
R
R
C
2R
R
B
R
R
2R
A
D
2R
A
R
Req. � R
B
C
R
B
Unidade B
Capítulo da
7 Associação
de3resistores
Os fundamentos
Física • Volume
• Capítulo 7
os fundamentos
da física
T.151
3
33
Testes
propostos
Resoluções
dos
testes propostos
Resposta: e
No circuito, temos:
i' � 2 A
i � i’ � i’’
i�4A
C
4 � 2 � i’’
i’’ � 2 A
6Ω
i''
6Ω
3Ω
Como i’ � i’’, temos:
4A
12 Ω
D
R
U
12 Ω � 3 Ω � R ⇒ R � 9 Ω
Utilizando a lei de Ohm:
U � Req. � i ⇒ U � 18 Ω � 4 A ⇒ U � 72 V
T.152
Resposta: e
Se o reostato estiver regulado no seu valor mínimo (R � 0), o resistor de 20 kΩ
estará em curto-circuito e a intensidade de corrente será máxima:
U � R1 � imáx.
Sendo U � 100 V e R1 � 10 kΩ � 10 � 103 Ω, vem:
100 � 10 � 103 � imáx. ⇒ imáx. � 10 � 10�3 A ⇒
imáx. � 10 mA
Se o reostato estiver regulado no seu valor máximo (R � 20 kΩ), a intensidade de
corrente será mínima. O circuito correspondente será:
10 kΩ
100 V
20 kΩ
20 kΩ
3
R2 = 20 kΩ = 20 • 10 Ω
10 kΩ
10 kΩ
100 V
10 kΩ
Aplicando a lei de Ohm:
U � R2 � imín. ⇒ 100 � 20 � 103 � imín. ⇒ imín. � 5,0 � 10�3 A ⇒
imín. � 5,0 mA
Unidade B
Capítulo da
7 Associação
de3resistores
Os fundamentos
Física • Volume
• Capítulo 7
os fundamentos
da física
T.153
3
44
Testes
propostos
Resoluções
dos
testes propostos
Resposta: a
B
B
R
A
B
R
A
A
i
A
R
B
R
R
R
4
R
V
B
R
R
A
B
B
A
A
V�
T.154
R
�i ⇒
4
i�
4V
R
Resposta: e
3Ω
i1
A
i
i2
8Ω
6Ω
B
A
10 Ω
C
UAB
B
i
UAB
Pot � R � i 12 ⇒ 27 � 3 � i 12 ⇒ i1 � 3 A
UAC � 3 � i1 � 6 � i2 ⇒ 3 � 3 � 6 � i2 ⇒ i2 � 1,5 A
i � i1 � i2 ⇒ i � 3 � 1,5 ⇒ i � 4,5 A
UAB � Req. � i ⇒ UAB � 10 � 4,5 ⇒ UAB � 45 V
T.155
Resposta: e
i
2
O resistor entre C e B é o que dissipa maior
R
A
potência:
2
Pot � R � i � 32 W
R
C
i
R
B
i
i
2
Os dois resistores em paralelo são percorridos por correntes de intensidades i e
2
dissipam, cada um:
2
i
R � i2
�8W
Pot’ � R �   �
 2
4
A potência total dissipada será:
Pottotal � 32 W � 8 W � 8 W ⇒ Pottotal � 48 W
Unidade B
Capítulo da
7 Associação
de3
Os
fundamentos
Física
•• Capítulo
Os fundamentos
da
Física •• Volume
Volume
3resistores
Capítulo 7
7
os fundamentos
da física
T.156
T.153
3
Testes
propostos
Testes
propostos
Resoluções
dos
testes propostos
Resposta: ca
B
A 0,2 A e i2 � 0,1
Do gráfico,
A A
B para U � 40 V, temos: i1 �
Logo:R
B
R
i
i � i1 � i2 ⇒ i � 0,2 � 0,1 ⇒ i � 0,3 A
A
A
R
R
R
R
4
R
Pot � U � i ⇒ Pot � 40 � 0,3 ⇒ Pot � 12 W
B
V
B
R
T.157
5
54
R
B
B
Resposta:
b
A
A
A
Na situação em que U1 � 110 V, os dois resistores ficam associados em paralelo e
R
4V é R1 � R . Logo, a potência será dada por:
a resistência
V
�
� i ⇒equivalente
i�
2
4
R
U12
2U12
⇒ P(110) �
R
R
Resposta:2e
P(110 ) �
T.154
�
Na situação em
3 Ω que U2 � 220 V, os dois resistores ficam associados em série e a
i1
resistência
equivalente é R28 �
2R. Logo, a potência
será dada por:
10 Ω
Ω
A
i
C
i U22 6 Ω
⇒ P(220) �
2R
UAB
P( 220 ) �2
(2U1)
B
A
2
2R
Comparando � e �, vem:
⇒ P(220) �
B
2
4Ui 1
2R
U
⇒ P(220) �
AB
2
2U 1
R
�
Pot � R � i 12 ⇒ 27 � 3 � i 12 ⇒ i1 � 3 A
P(220) � P(110)
UAC � 3 � i1 � 6 � i2 ⇒ 3 � 3 � 6 � i2 ⇒ i2 � 1,5 A
i � i1 � i2 ⇒ i � 3 � 1,5 ⇒ i � 4,5 A
T.158
T.155
U
Resposta:
AB � Req. �ei ⇒ UAB � 10 � 4,5 ⇒ UAB � 45 V
U2
, vem:
De Pot �
R
Resposta:
e2
(110)
Pot �
�
O resistor2Rentre C e B é o que dissipa maior
potência:
(220)2
(220)2
Pot ’ �
⇒ Pot ’ �
2 2 �
R Pot � R � i � 32 W
R
2
i
2
R
A
�
R
C
i
De � e �, temos:
R
B
i
i
2
Os
resistores
são percorridos por correntes de intensidades i e
2 � (220)2em paralelo
Potdois
’
2R
�
�
2
Pot
R
(110)2
dissipam, cada um:
2
2 
Pot ’
Pot
 220
2 ’
�R4� �i  �
�W
16
 R⇒� i � 8
Pot’
�




Pot
 2110

4 Pot
A potência
será:
Pot’
� 16 � total
Pot ⇒dissipada
Pot’ � 16
� 550 ⇒ Pot’ � 8.800 W
Pottotal � 32 W � 8 W � 8 W ⇒ Pottotal � 48 W
Unidade B
Capítulo da
7 Associação
de3resistores
Os fundamentos
Física • Volume
• Capítulo 7
os fundamentos
da física
T.159
3
Testes
propostos
Resoluções
dos
testes propostos
Resposta: e
O circuito dado pode ser esquematizado como segue:
R1
0,8 A
0,4 A
A
0,4 A
B
16 Ω
20 V
14 Ω
0,3 A
D
R2
C
0,8 A
0,5 A
Podemos concluir que:
R1 � 16 Ω
UAB � 16 � 0,4 ⇒ UAB � 6,4 V
No resistor de 14 Ω:
UBC � 14 � 0,8 ⇒ UBC � 11,2 V
Como U � 20 V corresponde à soma das ddps, vem:
U � UAB � UBC � UCD ⇒ 20 � 6,4 � 11,2 � UCD ⇒ UCD � 2,4 V
No resistor R2, temos:
UCD � R2 � i2 ⇒ 2,4 � R2 � 0,5 ⇒ R2 � 4,8 Ω
Logo, a potência dissipada em R2 será:
Pot2 � R2 � i 22 � 4,8 � (0,5)2 ⇒ Pot2 � 1,2 W
ou
Pot2 � UCD � i2 � 2,4 � 0,5 ⇒
Pot2 � 1,2 W
66
Unidade B
Capítulo da
7 Associação
de3resistores
Os fundamentos
Física • Volume
• Capítulo 7
os fundamentos
da física
T.160
3
Testes
propostos
Resoluções
dos
testes propostos
Resposta: a
Vamos calcular as resistências elétricas das lâmpadas com os dados nominais:
lâmpada L1: R1 �
(12)2
U2
⇒ R1 �
⇒ R1 � 72 Ω
Pot1
2
lâmpada L2: R2 �
(12)2
U2
⇒ R2 �
⇒ R2 � 36 Ω
Pot 2
4
lâmpada L3: R3 �
(12)2
U2
⇒ R3 �
⇒ R3 � 24 Ω
Pot3
6
Assim, temos:
72 � 36 Ω � 24 Ω
72� 36
72 Ω
A
i
L1
i
24 Ω
L3
36 Ω
B
A
Req. � 48 Ω
B
i
L2
U � 12 V
U � 12 V
U � Req. � i ⇒ 12 � 48 � i ⇒ i � 0,25 A � 2,5 � 10�1 A
T.161
Resposta: e
Quando a ligação é em série, temos:
Rs � 2R (sendo R a resistência de cada lâmpada)
Logo, a potência dissipada é dada por:
Ps �
U2
U2
⇒ Ps �
2R
Rs
�
Na associação em paralelo: Rp �
R
2
Logo, a potência dissipada vale:
Pp �
U2
2U 2
U2
⇒ Pp �
⇒ Pp �
R
Rp
R
2
Comparando � e �, vem: Pp � 4Ps
Como Ps � 200 W, vem: Pp � 800 W
�
77
Unidade B
Capítulo da
7 Associação
de3resistores
Os fundamentos
Física • Volume
• Capítulo 7
os fundamentos
da física
T.162
T.162
88
8
da Física • Volume 3 • Capítulo 7
3Os fundamentos
Testes
propostos
Resoluções
dos
testes propostos
Testes propostos
Resposta: b
Resposta:
b
O
fusível suporta
uma corrente elétrica de intensidade 15 A e a tensão elétrica no
O
fusíveldoméstico
suporta uma
corrente
15 A e máxima
a tensão suportada
elétrica no
circuito
é de
110 V.elétrica
Assim,dea intensidade
potência elétrica
circuito
doméstico
de 110 V. Assim, a potência elétrica máxima suportada
no circuito
será dadaé por:
no circuitoPot
será
dada por:
máx. � U � imáx. ⇒ Potmáx. � 110 � 15 ⇒ Potmáx. � 1.650 W
� imáx.
Potmáx.será
� 110
� 15 ⇒
W
máx. � U
máx. � 1.650
A potênciaPot
máxima
total
do⇒circuito
a soma
daPot
potência
da lâmpada
(PotL )
A
potência
máxima
totaldo
doferro
circuito
será a (Pot
soma
da potência da lâmpada (PotL )
com
a potência
máxima
de passar
Fe ). Assim temos:
com a potência máxima do ferro de passar (PotFe ). Assim temos:
Potmáx. � PotL � PotFe ⇒ 1.650 � 150 � PotFe ⇒ PotFe � 1.500 W
Potmáx. � PotL � PotFe ⇒ 1.650 � 150 � PotFe ⇒ PotFe � 1.500 W
T.163
T.163
Resposta: c
Resposta:
c
O
maior aquecimento
corresponde à menor resistência, em vista da fórmula
O maior2 aquecimento corresponde à menor resistência, em vista da fórmula
U
Pot � 2 , mantendo-se U constante. Assim, temos:
UR
Pot �
, mantendo-se U constante. Assim, temos:
R
Aquecimento
Resistência
Associação
Aquecimento
Resistência
Associação

R
máximo
⇒
mínima
⇒
em paralelo  Req. � 

R
2
máximo
⇒
mínima
⇒
em paralelo  Req. � 
mínimo
⇒
máxima
⇒
em série (Req. � 2R) 2
mínimo
⇒
máxima
⇒
em
eq. � 2R)
intermediário
⇒
intermediária
⇒
um série
único(Rresistor
(Req. � R)
intermediário
T.164
T.164
⇒
intermediária
⇒
um único resistor (Req. � R)
Resposta: d
Resposta:
A
potênciadelétrica máxima suportada pelo circuito será:
A
elétrica máxima suportada pelo circuito será:
Potpotência
máx. � U � imáx. � 220 � 30 ⇒ Potmáx. � 6.600 W
Potmáx. � U a� itorneira
� 30 ⇒
Potmáx.
W
máx. � 220
Ligando-se
elétrica
(2.000
W)�e6.600
o chuveiro
(2.200 W, verão, e 4.000 W,
T.165
T.165
Ligando-se
torneira
elétrica
(2.000 W) e o chuveiro (2.200 W, verão, e 4.000 W,
inverno), o afusível
não
queimará.
inverno), o fusível não queimará.
Resposta: d
Resposta:Ld1:
Lâmpada
Lâmpada
Pot1 � U1 L� 1i:1 ⇒ 0,6 � 3 � i1 ⇒ i1 � 0,2 A
Pot1 � U1 L� 2i:1 ⇒ 0,6 � 3 � i1 ⇒ i1 � 0,2 A
Lâmpada
Lâmpada
L:
Pot
2 � U2 � 2i2 ⇒ 0,3 � 3 � i2 ⇒ i2 � 0,1 A
Pot
2 � U2 � i2 ⇒ 0,3 � 3 � i2 ⇒ i2 � 0,1 A
Resistor:
Resistor:
i3 � i1 � i2 � 0,1 A
i3 � i1 � i2 � 0,1 A
U � R � i3 ⇒ 3 � R � 0,1 ⇒ R � 30 Ω
U � R � i3 ⇒ 3 � R � 0,1 ⇒ R � 30 Ω
i1
6V
6V
i1
i1
L1
i1
L1
3V
i2
3V 3V
i2L
3V
i3
2
iR
3 , 3V
L2
R, 3 V
R
Comparando:
R � R ; R2 �P1 1 ; R3 = 2R1
P
1 � P4 ; P2 � 2 1� P1 ;4P3 �
22
Unidade
B a potência dissipada é inversamente proporcional à
Mantida
Portanto,constante
temos: a tensão,
Capítulo da
7 Associação
de3resistores
Os fundamentos
Física • Volume
• Capítulo 7

U2 
P2 � P1 � P4 � P3
os fundamentos
resistência  P �
 . Assim:
Testes
propostos
da física
dos
testes propostos
RResoluções


3
T.166
T.167
T.166
T.167
T.168
T.168
T.167
T.167
T.168
T.168
9
99
P
P1 � P4 ; P2 � 2 � P1 ; P3 � 1
Resposta: d
e
2
Portanto,
Sendo
ρ a temos:
resistividade
doL material de que é feito o filamento das lâmpadas, temos,
U2
Pot � Osefundamentos
�ρ�
R
da Física • Volume
• CapítuloB7 (de filamento mais gros- 9
De
, concluímos
que a3 lâmpada
para a resistência
de cada
R
APuma:
2 � P1 � P4 � P3
propostos
so) tem
menor
resistência
e,Testes
portanto,
maior potência. Logo, brilha mais.
ρ
�
L
ρ
�
L
R11 �
; R22 �
; R33 � ρ � 2 � L ; R 44 � ρ � 2 � L � ρ � L
S
2S
2S
S
S
e R1 � R4 ; R2 � R11 ; R3 = 2R1
Resposta: d
Comparando:
1 � 01
4
2
3
1
Resposta: soma
2
2
Sendo ρ a resistividade
doL material
de que é feito o filamento das lâmpadas, temos,
U
(01)PotCorreta.
�constante
�
e R �aρtensão,
De
, concluímos
a lâmpada
B (de filamento
mais gros-à
Mantida
a potênciaque
dissipada
é inversamente
proporcional
para a resistência
de cada
R
A 2uma:
2
2
U e, portanto, maior potência. Logo, brilha mais.
 de
UPot
so) tem
resistência
, menor
corresponde
resistência, sob
Em
ρ �menor
Lvista
ρ � L.�Assim:
ρ � 2 � potência
ρ�2�L
ρa� maior
L
L
P
�
resistência

R1 �
; R2 � R
; RR3 �
; R4 �
�


S
2S
2S
S
S
mesma ddp.
P11R1
; R3 = 2R1
Comparando:
R1��
�
R;4P; 33R�
(02)
�2
P1101
P
2 �
1 � PIncorreta.
4 ; P2
2soma
Resposta:
1
4
22
lei de Ohm (U � R � i ), pelo resistor de maior resistência (lâmpada de
(01) Pela
Correta.
Mantida
constante
Portanto,
temos: a tensão, a potência dissipada é inversamente proporcional à
60 W) passa a menor2 intensidade de corrente.
2
UP � P � P � P
 de UPot
�Assim:
potência
Em
vista
2 , menor
1
4
3 corresponde a maior resistência, sob
1
4
3
(04) Incorreta.
P
�
.
resistência


R2
R 

Como
lâmpadas estão associadas em paralelo sob ddp constante, a queima
mesmaasddp.
P1 altera a corrente na lâmpada de 100 W, que mantém
da
lâmpada de 60 W não
Incorreta.
P(02)
1 � P4 ; P2 � 2 � P1 ; P3 �
2
Resposta:
d
seu brilho
Pela
lei de normal.
Ohm (U � R � i ), pelo resistor de maior resistência (lâmpada de
2
Portanto, temos:
U 2passa
(08)Pot60
Incorreta.
a menor
intensidade que
de corrente.
�W)
ρ � L , concluímos
eR�
De
a lâmpada B (de filamento mais grosR
A
P
�
P
�
P
�
P
A
corrente
nos
fios
da
tomada
diminui
de (i60 � i100) para i100.
2
1
4
3
(04) Incorreta.
so)
tem
menor
resistência
e,
portanto,
maior
potência. Logo, brilha mais.
(16) Como
Incorreta.
as lâmpadas estão associadas em paralelo sob ddp constante, a queima
A resistência
elétrica
da lâmpada
é modificada
de modo
queW,dissipe
100 W
da
lâmpada de
60 W não
altera a corrente
na lâmpada
de 100
que mantém
Resposta:
d
parabrilho
o
circuito
para o qual foi fabricada.
seu
normal.
Resposta:
soma
� 01
2
U
L
(08)PotCorreta.
Incorreta.
(01)
�
eR�ρ�
De
, concluímos que a lâmpada B (de filamento mais grosR
2 tomada diminui de (i60 � i100) para i100.
A corrente
nos fiosAda
2
U
so)
menor
resistência
maior potência.
Logo,
brilharesistência,
mais.
Pot � e,, portanto,
menor potência
corresponde
a maior
sob
Em
vista de
(16)tem
Incorreta.
R
A resistência
mesma
ddp. elétrica da lâmpada é modificada de modo que dissipe 100 W
o
circuito
para o qual foi fabricada.
(02) para
Incorreta.
Resposta:
soma
� 01
lei de Ohm (U � R � i ), pelo resistor de maior resistência (lâmpada de
(01) Pela
Correta.
60 W) passa a menor2 intensidade de corrente.
U
, menor potência corresponde a maior resistência, sob
vista de Pot �
(04) Em
Incorreta.
R
Como
lâmpadas estão associadas em paralelo sob ddp constante, a queima
mesmaasddp.
lâmpada de 60 W não altera a corrente na lâmpada de 100 W, que mantém
(02) da
Incorreta.
seu
Pelabrilho
lei de normal.
Ohm (U � R � i ), pelo resistor de maior resistência (lâmpada de
(08) 60
Incorreta.
W) passa a menor intensidade de corrente.
A
corrente
60 � i100
100) para i100.
100.
(04) Incorreta. nos fios da tomada diminui de (i60
Incorreta.
(16) Como
as lâmpadas estão associadas em paralelo sob ddp constante, a queima
A
resistência
elétrica
da lâmpada
é modificada
de modo
queW,dissipe
100 W
da lâmpada de
60 W não
altera a corrente
na lâmpada
de 100
que mantém
parabrilho
o circuito
para o qual foi fabricada.
seu
normal.
(08) Incorreta.
A corrente nos fios da tomada diminui de (i60 � i100) para i100.
Unidade B
Capítulo da
7 Associação
de3resistores
Os fundamentos
Física • Volume
• Capítulo 7
os fundamentos
da física
T.169
3
10
10
Testes
propostos
Resoluções
dos
testes propostos
Resposta: d
Lâmpadas concebidas para uma tensão de 120 V, quando ligadas numa rede de
127 V, dissipam maior potência; conseq entemente apresentam maior intensidade luminosa e sua durabilidade diminui.
T.170
Resposta: e
i
Sendo i � i1 � i2, concluímos que a lâmpada L4
i2
possui o maior brilho. L2 e L3 têm brilho igual, mas
L1 brilha mais que L2.
i1
R
L2
R
L3
U
R
R
L1
i
L4
T.171
Resposta: c
Ligação I:
Na ligação I, as lâmpadas estão sob tensão de 110 V, que é a tensão nominal. L1,
L2 e L3 dissipam, respectivamente, as potências 20 W, 100 W e 500 W. Logo, na
ligação I, a lâmpada L3 apresenta maior brilho.
Ligação II:
Por meio dos valores nominais, calculamos as
i2
M
i1
R2
L2
R1
L1
resistências das lâmpadas:
N
i3
R3
L3
R1 �
(110)2
U2
⇒ R1 �
⇒ R1 � 605 Ω
Pot1
20
R2 �
(110)2
U2
⇒ R2 �
⇒ R2 � 121 Ω
Pot 2
100
R3 �
(110)2
U2
⇒ R3 �
⇒ R3 � 24,5 Ω
Pot3
500
110 V
Na ligação II, R1 é a maior resistência e é percorrida pela maior corrente. Logo, a
lâmpada L1 dissipa a maior potência e brilha mais.
Ligação III:
Na ligação III, todas as lâmpadas são percorridas pela mesma corrente. A lâmpada L1 dissipa a maior potência por ter a maior resistência. Logo, ela brilha mais.
Unidade B
Capítulo da
7 Associação
de3resistores
Os fundamentos
Física • Volume
• Capítulo 7
3
os fundamentos
da física
T.172
11
11
Testes
propostos
Resoluções
dos
testes propostos
Resposta: b
No esquema da alternativa b, quando uma lâmpada queima, as demais lâmpadas
do segmento a que ela pertence se apagam. Cada lâmpada dos outros segmentos
fica sob mesma tensão e suas luminosidades não se alteram.
T.173
Resposta: d
Chave Ch aberta
R
i
i
L1
U
R
L2
i�
R
L3
U
2R
Ch
Chave Ch fechada
R
I
U
I2
L1
L2
I�
I3
R
L3
R
Ch
Fechando a chave Ch, resulta:
I � i (o brilho de L1 aumenta)
I2 � i (o brilho de L2 diminui)
U
R
R�
2
I2 � I3 �
⇒ I�
I
U
�
2
3R
2U
3R