Capítulo 4 Interação Radiação-Matéria - Infis-UFU

UNIVERSIDADE FEDERAL DE UBERLÂNDIA
INSTITUTO DE FÍSICA
ESTUDO DA INTERAÇÃO RADIAÇÃO-MATÉRIA
COM APLICAÇÃO EM ELETRODINÂMICA
QUÂNTICA DE CAVIDADES.
GUSTAVO BORGES COELHO
Julho de 2011
1
GUSTAVO BORGES COELHO
ESTUDO DA INTERAÇÃO RADIAÇAO-MATÉRIA COM APLICAÇÃO EM
ELETRODINÂMICA QUÂNTICA DE CAVIDADES.
Monografia apresentada à coo rdenação
do curso de Física de Materiais da
Universidade Federal de Uberlândia
como requisito parcial para obtenção do
título
de
bacharel
em
Física
de
Materiais.
Orientador:
Duzzioni.
Prof.
Uberlândia-MG
2011
Dr.
Eduardo
Inácio
2
ESTUDO DA INTERAÇÃO RADIAÇAO-MATÉRIA COM APLICAÇÃO EM
ELETRODINÂMICA QUÂNTICA DE CAVIDADES.
Monografia
APROVADA
pela
coordenação do curso de Física de
Materiais da Universidade Federal de
Uberlândia.
Área
de
concentração:
Quântica, Informação Quântica.
Banca Examinadora
Prof. Dr. Eduardo Inácio Duzzioni (Orientador)
Prof. Dr. Jose Maria Villas-Bôas
Prof. Dr. Cristiano Alves Guarany
UBERLÂNDIA, 07 de Julho de 2011
Física
3
Dedica tó ria
Dedico este trabalho de conclusão de curso
aos meus queridos pais. Foram eles que
dispensaram a mim todos os recursos
imagináveis durante a graduação do curso
de física de materiais, bem como nas
demais etapas da minha vida.
4
Agradecimento s
Embora possa parecer um lugar comum: o enaltecimento dos pais pelo cumprimento de
uma etapa importante na vida dos seus filhos. É inconcebível não atribuir a eles: Wesley e
Cida todos os méritos que me permitiram ingressar, cursar e graduar em física de materiais
pela UFU. É sem dúvidas, devido aos seus exemplos de amor, dedicação e honradez que foi
possível cumprir um dos processos mais relevantes da minha formação.
Em um plano à parte, devo agradecer ao meu melhor amigo, aquele a quem se deve delegar
a causa primeira de todas as coisas. A ele, todos os meus agradecimentos entre outros diversos
fatores, pelo fornecimento de faculdades como, o raciocínio lógico, o discernimento e o juízo
de valor, que foram os principais recursos que me conduziram a conclusão deste curso.
Obrigado pai!
A todos os colegas que participaram de forma construtiva e agradável durante esses anos de
curso. Se fosse citar todos os nomes, eles certamente iriam ocupar boa parte desta seção, mas
não posso deixar de destacar a participação dos meus amigos Augusto e Fernando em vários
momentos de colaboração nos estudos e pelas incontáveis conversas que descontraíram um
ambiente por vezes tenso.
Por fim, devo agradecimentos a todo corpo docente da UFU, notadamente aos membros do
Infis, pela influência proveniente de suas formações construídas a base de disciplina e méritos.
Dentre eles, o professor Eduardo Inácio Duzzioni foi indubitavelmente, o responsável pelo
empreendimento da maior parte de informações técnicas por mim assimiladas, além de
constituir um modelo de dedicação e conhecimentos profundos à cerca da física. Este
trabalho, só foi possível graças a sua orientação que para a discussão e esclarecimento de
várias dúvidas sempre encontrou nele uma figura disponível e atenta.
5
RESUM O
Este trabalho visa estudar o comportamento físico da interação radiação-matéria, a partir
dos modelos semi-clássico e quântico. Para compreendê-los precisamente foi realizada uma
abrangente revisão acerca das ferramentas matemáticas da mecânica quântica. Posteriormente,
estudou-se a interação considerando estes dois modelos: inicialmente os níveis atômicos são
quantizados enquanto o campo de radiação era concebido em termos de uma visão clássica.
Pretendendo uma análise comparativa, tanto o átomo quanto o campo foram examinados
quanticamente. Algumas diferenças apreciáveis entre estas duas vertentes como, por exemplo,
a emissão espontânea e o aparecimento de colapsos e ressurgimentos são apresentadas. Por
fim, é relatado um experimento que certifica a natureza granular do campo de radiação.
6
ABSTRACT
This work aims to study the physical behavior of radiation-matter interaction, from a semiclassical point of view and a quantum models. To understand them precisely was done on a
comprehensive review of the mathematical tools of quantum mechanics. Subsequently, we
studied the interaction considering these two models: first the atomic levels are quantized
while the radiation field was conceived in terms of a classical view. Then a comparative
analysis, both the atom and the quantum field were examined. Some appreciable differences
between the two wings, for example, spontaneous emission and the appearance of collapses
and revivals are presented. Finally, we describe an experiment that certifies the granular
nature of the radiation field.
7
LISTA DE FIGURAS
4.1 – Representação de um átomo cuja frequência
de transição entre dois níveis é
ressonante ou aproximandamente ressonante a um campo de radiação de radiação de
frequência
............................................................................................................................ 30
4.2 – Representação da variação de energia para um átomo de dois níveis com frequência de
transição
............................................................................................................................ 35
4.3 – Sistema de eixos coordenados, em que o núcleo atômico dista
da origem e δ alude
δ .
ao raio que o elétron descreve em torno do núcleo. Nesta configuração,
................................................................................................................................................ 37
5.1 – Gráfico da probabilidade de transição do elétron de valência entre os níveis fundamental
e excitado segundo a teoria semi-clássica........................................................................... .. 54
5.2 – Gráfico da inversão de população gerado pela interação do campo de radiação coerente
com um átomo de dois níveis no estado excitado ................................................................
57
5.3 – Gráfico da inversão de população supondo que a radiação coerente seja contínua,
obedecendo a expressão
chamada
função
gama
, onde
e
corresponde
ao
fatorial
de
,
para
é
números
naturais................................................................................................................................... 58
5.4 – Esquema do aparato experimental utilizado por S. Haroche e colaboradores [13] ..... 59
5.5 – De A - D são mostradas as inversões de população considerando os estados iniciais
,
,
,
, respectivamente. De a – d
são mostradas as transformadas de Fourier dos gráficos A – D, respectivamente. As
freqüências ,
,
e
estão indicadas pelas linhas pontilhadas [15] ....................... 62
B-1 – Símbolo de Levi-Cevita ............................................................................................ 66
8
LISTA DE TABELAS
2.1 – Resumo da notação padrão utilizada em mecânica quântica para conceitos de álgebra
linear. Este tipo de notação é chamado de notação de Dirac [3]........................................... 22
B-1– As matrizes de Pauli. Algumas vezes
é omitida da lista, e somente
,
,e
são
referidas como matrizes de Pauli [3]...................................................................................... 66
9
SUMÁRIO
1 Introdução
11
2 Bases matemáticas da mecânica quântica
13
2.1 – Bases e independência linear .................................................................................... 13
2.3 – Operadores lineares e matrizes .................................................................................. 14
2.3 – Produto interno ........................................................................................................... 15
2.4 – Autovalores e autovetores ..................................................................................... ... 17
2.5– Operadores adjuntos .................................................................................................. 19
2.6 – Produto Tensorial ..................................................................................................... 20
3 Postulados da mecânica quântica
23
3.1 – Postulado 1............................................................................................................... 23
3.2 – Postulado 2............................................................................................................... 25
3.3 – Postulado 3............................................................................................................... 27
3.4 – Postulado 4............................................................................................................... 28
4 Interação radiação-matéria
30
4.1 – O campo de radiação................................................................................................. 31
4.4 – Modelo semi-clássico................................................................................................ 32
4.2.1 – Segunda quantização do termo do elétron..................................................... 33
4.2.2 – Segunda quantização do termo de interação................................................... 36
4.2.3 – A representação de interação e a aproximação de onda girantes .................. 40
4.2.4 – Determinação da dinâmica do sistema.......................................................... 43
10
4.3 – Teoria quâtica para a descrição da interação radiação matéria............................... 45
4.3.1 – Quantização do campo de radiação.............................................................. 45
4.3.2 – Hamiltoniano quântico da interação átomo-campo..................................... 47
4.3.3 – O modelo de Jaynes-Cummings.................................................................
50
4.3.4 – Dinâmica no modelo de Jaynes-Cummings................................................
51
5 Resultados e discussões
53
5.1 – Análise teórica ........................................................................................................... 53
5.2 – Um experimento para testar a quantização do campo de radiação ........................... 58
6 Conclusões
63
7 Apêndices
64
A – Partícula carregada imersa em um campo eletromagnético ............................................ 64
B – Matrizes de Pauli e suas conexões com operadores de pseudo-spin e eletrônicos .......... 66
C – Solução analítica da equação de Schr dinger para o hamiltoniano radiação-matéria no
regime semi-clássico ............................................................................................................. 69
8 Referências Bibliográficas
73
11
Capítulo 1
Introdução
A afirmação da física quântica como uma área que fornece resultados fiéis ao
comportamento de partículas atômicas provocou um grande alvoroço na primeira metade do
século XX. Esse novo campo científico introduzia conceitos até então renegados pelos físicos
clássicos e se utilizava eminentemente de formulações matemáticas para descrever o
funcionamento dos seus objetos alvo: átomos e seus constituintes, elementos que compõem
toda a matéria conhecida na natureza, além dos fótons, pacotes (quanta) de energia da luz.
Este trabalho se apóia em fundamentos fornecidos pela mecânica quântica a fim de prover
uma descrição precisa a cerca de um átomo sujeito à incidência de radiação eletromagnética.
Antes, porém de ingressar propriamente no assunto, foi discutido as técnicas matemáticas da
mecânica quântica. Estes fundamentos frequentemente geram dúvidas e confusões em alunos
a nível de graduação que desenvolvem estudos na área de ótica quântica, e além disso,
constitui uma parte vital para compreensão dos temas pertinentes a esse campo de pesquisa.
Justificando assim, a sua abordagem. Apoiado neste alicerce algébrico pode-se enunciar os
quatro postulados básicos da física quântica. A partir deles, o comportamento de quaiquer
sistema físico pode ser estudado. Devido a sua abrangência, este trabalho valeu-se das
predições provenientes dos postulados como base teórica para desenvolver uma aprofundada
revisão sobre um dos sistemas interagentes mais elementares já conhecidos, que consiste
pitorescamente na aplicação de luz sobre a matéria.
Para tanto, considerou-se a matéria sendo composta por um átomo no qual o elétron de
valência possui frequência de transição entre dois níveis eletrônicos particulares próxima à
frequência de incidência do campo de radiação. O mesmo, por sinal, foi sem dúvidas o
principal foco de estudo deste texto. Abordado meticulosamente pela teoria semi-clássica e
quântica, o campo pode então ser comparado sobre estas duas modalidades, originando
dicotomias flagrantes entre uma e outra. Fenômenos como a quantização da luz indicando um
caráter corpuscular para esta, previsto apenas pela mecânica quântica, foram verificados
experimentalmente no capítulo 5 no contexto da Eletrodinâmica Quântica de Cavidades
(EQC), colocando átomos de rubídio dentro de pequenas estruturas com a existência de um
12
único modo eletromagnético e alto fator de qualidade1. Concedendo definitivamente a esta
teoria a condição de uma preciosa ferramenta no trato de sistemas em escala espacial.
O trabalho está didaticamente dividido em outros cinco capítulos. No segundo, revisou-se
os conceitos matemáticos da álgebra linear que se faziam necessários para a compreensão dos
postulados da mecânica quântica, assunto este que confere título ao capítulo 3 que tratou
detalhadamente os princípios que regulam a estrutura da física de partículas de baixíssima
escala espacial. No capítulo 4, estudou-se intimamente o tema interação radiação-matéria,
resultando em dois modelos de energia para o sistema, inicialmente obteve-se o hamiltoniano
a nível semi-clássico que descreve a interação considerando apenas os níveis atômicos
quantizados e após uma análise inteiramente quântica foi deduzido o modelo de JaynesCummings. No quinto capítulo foram discutidas as conseqüências dos modelos supracitados,
incompatibilidades importantes foram percebidas e analisadas nesta discussão. Por fim, no
capítulo 6 são apresentadas as conclusões deste texto.
1
Uma definição mais elaborada sobre este conceito é dada no capítulo 5 quando se discute do experimento de
Haroche.
13
Capítulo 2
Bases ma temá tica s da mecâ nica quâ ntica
A mecânica quântica (M.Q.) é considerada por muitos estudiosos como a teoria mais
sofisticada já produzida pelo homem [1]. Ela é inteiramente fundamentada em uma linguagem
matemática que aliada a conceitos físicos fornece um arcabouço capaz de determinar o
comportamento de sistemas em escala atômica. Devido a esse caráter matemático, a M.Q. é
muitas vezes associada a uma estrutura de difícil compreensão por parte dos leitores. Tendo
em vista este fato, convém esclarecer, neste trabalho alguns conceitos associados à álgebra
linear, base teórica na qual se sustentam os postulados da M.Q..
2.1 – Bases e independência linear
Dados dois vetores
segundo as direções de
direções são as de
e
e
encontrar dois números
não-colineares2, qualquer vetor
e
. O problema consiste em determinar dois vetores cujas
e cuja soma seja
e
pode ser decomposto
[2]. Em outras palavras, é necessário
, tais que:
(2.1)
Ou genericamente
Quando o vetor
e
está representado desta forma diz-se que este é combinação linear de
O par de vetores
Os vetores não nulos
conjunto de números complexos
2
e
é chamado de base.
são linearmente independentes se e somente se existir um
com
, onde
, tal que:
Dois vetores
e
são colineares se pertencerem à mesma direção. Ou seja, caso pssuam segmentos de reta
situados sobre uma mesma reta ou a retas paralelas.
14
,
(2.3)
neste caso, o número de vetores linearmente independente define a dimensão do espaço.
2.2 – Operadores lineares e matrizes
Um operador pode ser entendido como uma função
que a cada vetor de entrada
pertencente ao espaço vetorial V produz um novo vetor de saída
pertecente a V. A
linearidade de um operador Ô qualquer se deve ao fato deste obdecer a seguinte propriedade:
Ô
, com
operadores lineares  e
i)
ii)
iii)
=
e
num espaço S de vetores
satisfazem as seguintes relações:
equivale a
equivale a
iv)
. Além disso, dois
;
(adição);
(multiplicação).
(potência de um operador).
Existe uma importante conexão que determina a representação de operadores lineares via
matrizes. Ela é estabelecida através da aplicação de um operador linear
relação resulta em um novo vetor
sobre
onde essa
. Ou seja,
.
(2.4 a)
A partir da equação (2.2), ratificou-se que qualquer vetor pode ser escrito em termos de uma
base. Assim:
Na última equação,
finita n e
Então se:
e
forma uma base ortonormal de um espaço vetorial
são as componentes de
e
de dimensão
, respectivamente, em relação a esta base.
15
A igualdade acima é satisfeita se:
onde
são os elementos da matriz de representação do operador linear
com relação a base
.
No caso mais geral, a relação entre
e
pode ser escrita matricialmente como:
,
onde:
;
e
.
2.3– Produto interno
Um produto interno é uma função que toma dois vetores de entrada
e
de um espaço
vetorial e produz um número complexo como saída. Em M.Q. utiliza-se a seguinte notação
para o uso do produto interno:
, em que
é o vetor dual de
O dual é um operador
linear que leva elementos do espaço V para números complexos C, definido como
(
[3]. Como será mostrada adiante a representação matricial de
um operador dual será uma matriz linha. Uma função
de V x V para C é um produto
interno se obdecer as seguintes propriedades:
1)
2)
3)
é linear no segundo argumento,
*=
, com a igualdade valendo se e somente se
Uma decorrência importante que segue e tem uma conexão direta com uma linguagem
largamente usada em M.Q., diz respeito ao espaço de Hilbert, que por sua vez, é definido
como um espaço vetorial munido de produto interno (espaço de produto interno).
16
Outras definições importantes que merecem ser ressaltadas são a de vetores ortogonais,
norma, vetor unitário e vetores ortonormais. Os vetores
e
são considerados ortogonais
se o seu produto interno for igual a zero. Por exemplo,
ortogonais, pois:
=
e
são
= 0.
Define-se a norma de um vetor por:
.
Um vetor unitário
é aquele para o qual
. Também se diz que tal vetor é
normalizado. A normalização de um vetor é feita dividindo-se o vetor por sua norma, de tal
modo que:
. Um conjunto de vetores
, sendo i um índice, é ortonormal se os vetores
distintos do mesmo conjunto forem ortogonais e se todos os vetores deste mesmo conjunto
forem unitários. Como exemplo ilustrativo vale recorrer novamente aos vetores da base
canônica
e
tanto o vetor
=1e
Verificou-se, acima que eles de fato são ortogonais e
como o vetor
=
são unitários, haja visto que
=
=
=
= 1. Do exposto acima, fica claro que todo conjunto de
vetores distintos que podem ser classificados como ortonormais, são consequentemente
ortogonais, porém a recíproca nem sempre é válida, isto é, para que vetores ortogonais
possam ser considerados ortornormais, faz-se necessário ainda verificar a condição de
unitariedade.
É possível ainda estabelecer uma conexão entre produto interno e sua representação
matricial. Escrevendo os vetores
e
, tal que
e
em termos da base ortonormal
, ou seja,
, então:
(2.6)
17
Um outro artifício que pode ser gerado a partir do uso do produto interno é o que se
conhece como representação de produto externo. Tal técnica surge através da consideração
da existência de dois vetores
respectivamente. Definindo
e
pertencentes aos espaços vetoriais V e W,
o operador linear de V para W cuja ação é dada por [3]:
.
(2.7)
A relação expressa por (2.7) pode ser corretamente interpretada a partir de dois resultados: o
primeiro manifesta a ação do operador
multiplicação
pelo complexo
sobre o vetor
Já o segundo implica na
.
A principal consequência do produto externo é o resultado denominado relação de
completitude. Seja
como
uma base ortonormal de V, tal que qualquer vetor
para algum conjunto de números
Como tal resultado é válido para qualquer
O operador
. Note
pode ser escrito
, e, portanto:
segue que
é conhecido como operador identidade e se mostra altamente relevante no palco
de qualquer espaço vetorial, mantendo invariante as operações em que ele atua.
2.4– Autovalores e autovetores
A idéia de autovalores e autovetores podem ser de suma importância na determinação das
energias e estados de um sistema físico. Dado um operador linear A em um espaço vetorial
tal que
em que
correspondente ao seu autovetor
é um número complexo conhecido como autovalor de
,
[3], é possível obter sua função característica dada por
. As soluções das equações características c(
são os autovalores do
18
operador A. Estabelecidos os autovalores e autoestados do operador A, pode-se reescrevê-lo
sob sua representação diagonal, que consiste em
onde os vetores
correspondentes
formam um conjunto de autovetores ortogonais de A, com autovalores
. Neste caso, diz-se que tal operador é diagonalizável.
A título de ilustração, convém detalhar o processo de obtenção de diagonalização do
operador de uma das matrizes de Pauli (apêndice B), por exemplo, a matriz
cuja equação
característica,
.
(2.10 a)
Fornece os seguintes autovalores,
e
Aplicando agora a definição acima:
.
(2.10 b)
para os valores de
e
,
respectivamente:
, o sistema admite solução do tipo:
Equivalentemente, considerando
. Então:
ou
:
ou
Neste ponto é interessante esclarecer que o resultado dos autovetores,
tipicamente associados em informação quântica a base ortonormal
Feito isso, os autovetores do operador
podem ser reescritos como:
e
e
, são
, respectivamente.
19
De acordo com a definição de representação diagonal, expressa em termos da equação (2.9),
Em que a representação matricial é escrita com relação à base ortonormal
e
. As
representações diagonais são algumas vezes chamadas de decomposições ortonormais.
2.5 - Operadores adjuntos
Suponha que
seja um operador linear sobre um espaço de Hilbert ℋ. Isso quer dizer que
existe um único operador linear
sobre ℋ, tal que todo vetor
e
.
a ℋ,
(2.11)
Esse operador linear é conhecido com adjunto ou conjugado hermiteano de . Pela definição
acima é fácil ver que
. De fato:
(2.12)
Por convenção,
sendo um vetor, então
. Com isso,
(2.13)
20
A representação matricial desse tipo de operador é realizada através da transposição
conjugada dos membros dessa matriz. Ou seja,
complexa, e
, em que * indica conjugação
remete a operação de transposição. Por exemplo,
(2.14)
Um operador
é dito normal se
. Claramente, um operador hermiteano3 é
também um operador normal.
Por fim, outro conceito relevante, é o de operador unitário. Dado um operador U, o mesmo
será denominado unitário, caso satisfaça a seguinte condição:
. Perceba que
assim como os operadores hermiteanos, operadores unitários também são enquadrados dentro
de uma classe mais ampla, já previamente discutida, conhecida como operadores normais.
Geometricamente, eles são importantes porque preservam o produto interno entre vetores [3].
Para ver isso, sejam
mesmo que entre
e
e
dois vetores, onde o produto interno entre U
e U
é o
,
(2.15)
2.6– Produto Tensorial
Como será visto na seção 3.4, a maneira como sistemas quânticos4 individuais se agregam
para formar sistemas compostos constitui o quarto postulado da M.Q.. Tal situação é
inteiramente descrita a partir da aplicação do produto tensorial ou produto direto entre os
vetores de estado que caracterizam cada sistema. Para melhor compreender esse conceito,
convém considerar a seguinte descrição:
3
O operador hermiteano é aquele cujo adjunto é igual ao próprio operador. Isto é,
. Por isso, essa classe
de operadores é também comumente chamada de auto-adjuntos.
4
Neste trabalho o termo sistema quântico será utilizado no sentido de descrever um conjunto de partículas que
possuem dimensão subatômica. Dessa forma, todo seu comportamento físico será tratado por uma teoria
devidamente apropriada, conhecida por mecânica quântica.
21
Sejam V e W espaços de Hilbert de dimensões M e N, respectivamente. Então V
combinações lineares do produto tensorial
entre os elementos
W são
de V e
de
W[3]. Em álgebra linear é comum o uso de outras notações para o produto tensorial desses
elementos. Por exemplo, representações abreviadas tais como:
utilizadas em substituição à expressão
,
,
são
.
Por definição o produto tensorial satisfaz as seguintes propriedades básicas:
1. Para um escalar z arbitrário e elementos
1. Para
2. Para
e
arbitrários em V e
arbitrário em V e
Supondo que
e
e
de V e
de W,
em W,
em W,
sejam matrizes de ordem
. Então a representação do produto
tensorial entre elas é a seguinte:
.
(2.16)
Uma outra notação geralmente encontrada na literatura envolvendo produtos tensoriais é
. Uma maneira de compreendê-la é por meio da “potenciação de um produto tensorial”,
no qual:
Assim para um estado
onde neste caso
, a operação:
.
é efetuada da seguinte maneira:
22
A seguir consta uma tabela que resume os principais conceitos até aqui discutidos
relacionando-os às suas representações matemáticas.
Tabela 2.1: Resumo da notação padrão utilizada em mecânica quântica para conceitos de álgebra
linear. Este tipo de notação é chamado de notação de Dirac [3].
Notação
Descrição
Conjugado complexo de z
Vetor. Também chamado de ket.
Vetor dual de
. Também chamado de bra.
Produto escalar entre
Produto tensorial entre
A*
e
.
e
.
Complexo conjugado da matriz A.
Transposta da matriz A.
Conjugado hermiteano, ou matriz adjunta de ,
Produto escalar entre
entre
e
eA
=(
)*
. Equivalente, ao produto escalar
23
Capítulo 3
Postulados da Mecânica Quântica
A teoria da M.Q. pode ser sintetizada em quatro regras básicas. Nelas, o comportamento de
sistemas em escalas atômicas é plenamente descrito em termos de uma linguagem matemática
que faz uso basicamente dos conceitos explorados no capítulo precedente. Como será visto
adiante, ao contrário da mecânica clássica alicerçada durante os séculos XVIII e XIX que
prevê resultados eminentemente determinísticos para sistemas macroscópicos [4], a M.Q.
estabelece uma visão probabilística acerca de sistemas subatômicos. Esta é uma distinção
notável entre as duas teorias. Enquanto a primeira é capaz de fornecer resultados consistentes
e indubitáveis a respeito do funcionamento de sistemas que podem ser vistos a olho nu, a
segunda prevê apenas a probabilidade que um determinado ente possuirá em estar num estado
físico específico. Na realidade, este fato é consequência da ação “intervencionista” do
observador neste tipo de sistema. Assim, a observação de experimentadores sobre essas
estruturas quânticas modifica o seu comportamento. Estas novidades aliadas a outras oriundas
dos postulados provocaram uma grande estranheza por parte dos físicos. No entanto, os testes
e confrontos que seguiram posteriormente a sua construção se mostraram altamente confiáveis
e concederam à M.Q. o status de uma teoria extremamente eficiente na análise de
nanoestruturas.
3.1 – Postulado 1.
O primeiro postulado utiliza-se dos conceitos abordados no capítulo anterior a fim de
determinar quais são os elementos envolvidos na descrição do objeto a ser estudado. De
acordo com a definição ele dita que:
A todo sistema físico isolado existe um espaço vetorial complexo com produto interno,
conhecido como espaço de estado do sistema. O sistema é totalmente descrito pelo seu vetor
de estado, um vetor unitário no espaço de estados.
O primeiro aspecto que deve ser discutido sobre o exposto acima se refere ao trecho “...
espaço vetorial complexo com produto interno...”. Na seção 2.3, verificou-se que tal espaço
24
recebe um nome peculiar, a saber: espaço de Hilbert. O estado, por sua vez é caracterizado
pela representação do que um observador conhece sobre o sistema em questão, sendo
habitualmente representado por
.
Um sistema quântico de particular interesse em informação quântica é o q-bit. Enquanto
um computador convencional usa bits clássicos para realizar o processamento de informação,
o computador quântico utiliza uma generalização do bit clássico: o bit quântico ou q-bit [5]. O
espaço de estado de um q-bit tem duas dimensões. Suponha que
e
formem uma base
ortonormal neste espaço. Um vetor de estado arbitrário deste sistema é escrito como:
a
(3.1)
em que a e b são números complexos. Segundo o primeiro postulado é necessário verificar
que
deva ser um vetor unitário, ou em outras palavras, que sua norma
. Logo:
.
(3.2)
A diferença entre um q-bit e um bit clássico está na possibilidade de haver superposições de
estados na forma a
[3]. Em tais casos não é possível determinar exatamente qual o
estado do sistema5. Isto é, o q-bit segundo as predições da M.Q. poderá ocupar
simultaneamente os estados
e
com um certo grau de probabilidade em cada caso.
Por fim, cabe lembrar que uma combinação linear
, com amplitudes
é uma superposição de
5
é uma superposição de estados
para cada um deles. Por exemplo, o estado:
e
, com amplitudes 1/
para
e -1/
para
.
A obtenção inequívoca do estado de um sistema quântico como, por exemplo, o q-bit está condicionado a
realização de infinitas medidas sobre o sistema, de tal forma que estas inúmeras medidas convirjam para um
estado específico. Devido as limitações nos modelos de medida, na prática é impossível afirmar com exatidão o
estado deste tipo de sistema.
25
3.2 – Postulado 2.
A importância do 2º postulado da M.Q. reside na possibilidade de se conhecer o estado
entre dois instantes de tempo. Literalmente ele é escrito como:
A evolução de um sistema quântico fechado é descrita por uma transformação unitária. Ou
seja, o estado
de um sistema está relacionado ao estado
unitário U que depende somente dos instantes de tempo
e
por um operador
:
(3.4)
É importante notar que o enunciado acima ressalta que o sistema quântico deve ser
estritamente fechado, ou seja, imune a qualquer interferência com o ambiente externo. Na
prática, isso não é possível. Qualquer ente físico é afetado pelo meio em que ele está inserido.
Contudo, em vários casos essa intervenção é mínima a ponto de ser desprezível, em uma boa
aproximação. Ademais, mesmo sistemas abertos podem ser descritos, a princípio, como partes
de um sistema fechado maior que evolui sob transformações unitárias.
Até aqui fora tratado somente a dependência entre dois instantes de tempo de um sistema
quântico qualquer. Mas caso o interesse seja em conhecer o processamento em tempo
contínuo do estado, o mecanismo utilizado será a equação de Schr dinger (E.S.):
onde ћ é a relação entre a constante de Planck (h
igual a 2π e
J.s) dividido por um fator
representa o operador hamiltoniano do sistema.
Como o hamiltoniano é um operador hermiteano, ele tem uma decomposição espectral
conforme a equação (2.9), que pode ser reescrita como:
com autovalores E e autovetores normalizados
chamados de auto-estados de energia, e
Os estados
são convencionalmente
é a energia associada ao estado
A menor
energia do sistema é chamada de energia do estado fundamental, e o auto-estado
correspondente de estado fundamental.
26
Como o uso da E.S. fornece toda a descrição da evolução em tempo contínuo de um estado
físico e a ação de operadores unitários permite o estudo da relação entre dois instantes de
tempo
e
deste mesmo estado. Uma questão que decorre desta constatação aponta sobre
um possível vínculo entre estas duas ferramentas. Para observar este fato, inicialmente é
necessário atentar-se à equação (3.4), na qual supõe-se que
e
. O uso da
série de Taylor6 em (3.4) se mostra de grande valia, à medida que permite reescrever a função
em termos de
, termo este presente na E.S.. Dessa maneira:
como dt representa um intervalo de tempo infinitesimal, o mesmo elevado ao quadrado pode
ser apropriadamente desconsiderado. De modo que
derivada temporal de
. E substituindo a primeira
em termos da expressão (3.5), que ratifica a conexão entre a
evolução do estado a partir do uso de operadores unitários e a equivalência com a E.S.,
Comparando esse resultado junto a equação (3.4), verifica-se que o operador unitário que
promove a evolução de um sistema quântico de acordo com a E.S., será:
Esse operador pode ainda ser reescrito sob uma nova versão. Para chegar até ela, é preciso
considerar que o intervalo de tempo que separa os instantes
intervalos infinitesimais, ou seja,
e
é subdividido em inúmeros
. Impondo que o limite de todas essas frações
infinitesimais tende ao infinito, é factível7 concluir que:
6
Em geral, séries de Taylor são utilizadas para avaliar o comportamento de uma função numa região pequena
em torno de um ponto.
7
Para chegar a expressão (3.11 b), basta tomar
, onde:
.
27
3.3 – Postulado 3.
O postulado 3 da M.Q. surge como consequência da intervenção de pesquisadores em
experimentos realizados sobre partículas microscópicas. Como visto na seção anterior este
tipo de ação imprimida sobre sistemas fechados acaba por intervir na sua natureza o tornando
então um sistema aberto. Com isso o uso de operadores unitários utilizados no estudo da
relação temporal do sistema não é mais justificável. Para a análise dessa situação o postulado
3 afirma que:
As medidas quânticas são descritas por determinados operadores de medida
. Esses
operadores atuam sobre o espaço de estados do sistema. O índice m se refere aos possíveis
resultados da medida. Se o estado de um sistema quântico for
imediatamente antes da
medida, a probabilidade de um resultado m ocorrer é dado por:
(3.10)
e o estado do sistema após a medida será:
Os operadores de medida satisfazem a relação de completitude:
Esta relação expressa o fato de que a soma das probabilidades deve ser igual a 1:
No primeiro postulado verificou-se que em M.Q. um sistema físico pode engendrar em dois
estados ao mesmo tempo. Para tanto, fora citado o q-bit
do bit clássico, ocupa os estados
e
a
que ao contrário
simultaneamente. A tal fenômeno é dado o nome
28
princípio de superposição. Neste momento, verificar-se-á quais são as previsões oriundas do
postulado 3. Ou seja, quais são os possíveis resultados que o q-bit
poderá ocupar após
efetuadas medidas sobre ele. Inicialmente, de acordo com a equação (3.14), o resultado “0” é
obtido com probabilidade:
Analogamente, o resultado “1” ocorre com probabilidade
. Os valores
encontrados anunciam um resultado inesperado, quando confrontado com o primeiro
postulado. Segundo ele um sistema quântico como o q-bit ocupa concomitantemente os níveis
definidos como 0 e 1 do sistema. Todavia, as expressões citadas são categóricas e mostram
que após realizadas medidas, o bit quântico pode ser visto apenas em 0 ou 1 com
probabilidades iguais a
e
, respectivamente.
3.4 – Postulado 4.
A importância do quarto postulado da M.Q. consiste na provisão do mecanismo que
possibilita a composição de dois ou mais sistemas físicos. Ele é enunciada da seguinte
maneira:
O espaço de estados de um sistema físico composto é o produto tensorial dos espaços de
estados dos sistemas físicos individuais. Se os sistemas de 1 até n, e o sistema i for preparado
no estado
decorre que o estado do sistema composto será
Um exemplo que esclarece esta proposição é o sistema descrito pelo vetor de estado,
.
29
que significa que
é formado pela superposição quatro estados em que cada um deles é
constituído pela união dos bits zero e um ou por uma combinação destes, apresentando ainda
amplitude igual a
.
30
Capítulo 4
Interação Radiação-Matéria
A forma como meios materiais respondem a incidência da radiação externa, sempre
despertou grande interesse da humanidade. E constitui uma área de pesquisa largamente
estudada, entre outras coisas, porque permite o conhecimento de várias propriedades destes
materiais, tais como o brilho, a cor, a transparência e a opacidade [6].
A interação entre a radiação e a matéria é consequência da força com que o campo elétrico
exerce sobre as cargas elétricas do átomo. Admitindo que o campo varie com uma certa
frequência
, a ação deste sobre a estrutura atômica tende a criar nas cargas um movimento
harmônico com a mesma frequência. Contudo, este movimento só será considerável se a
frequência do modo natural de vibração das cargas for aproximadamente igual à frequência do
campo. Neste estudo, considerar-se-á que a frequência do campo externo é ressonante ou
aproximadamente ressonante com a frequência de transição de dois níveis atômicos bem
definidos e a ocorrência de transições para outros níveis são praticamente improváveis através
do mesmo campo de radiação aplicado. Este tipo de estrutura é tipicamente conhecido como
átomo de dois níveis e está ilustrado na figura 4.1:
Figura 4.1: Representação de um átomo cuja frequência
de transição entre dois níveis é ressonante
ou aproximadamente ressonante a um campo de radiação externo de frequência
.
31
O problema será estudado a partir de dois modelos já conhecidos. Inicialmente, será feito
uso da teoria semi-clássica, em que apenas os níveis de transição atômica serão abordados sob
uma perspectiva quântica. Feito isso, tanto o campo de radiação como os níveis de transição
do atômo serão analisados quanticamente.
4.1 – O campo de radiação
Considere a existência de campos elétrico e magnético dentro de uma cavidade no vácuo.
Nesse contexto, as equações de Maxwell ficam sob a forma:
Uma maneira equivalente de expressar os campos elétricos e magnéticos é através da
utilização do potencial vetor eletromagnético e do potencial escalar eletromagnético, tal que:
A aplicação das equações (4.2) e (4.3) sobre (4.1 d), tratadas no calibre8 de Coulomb (
e
, haja visto que tal escolha mantêm invariantes as grandezas físicas envolvidas
no problema, conduz à seguinte relação:
8
A palavra calibre é proveniente do termo inglês gauge, sendo comum encontrar indiscrinadamente ambos os
termos na literatura.
32
da equação (4.4) obtém-se que
é igual a uma constante que será arbitrariamente escolhida
igual a zero, ou equivalentemente,
.
4.2 – Modelo semi-clássico.
A interação semi-clássica envolve um campo de radiação e um átomo cujos níveis de
energia são quantizados. Por conveniência, é adotado um campo de radiação monocromático
clássico a uma dada polarização,
,
(4.6)
incidindo sobre um átomo de dois níveis.
O hamiltoniano que fornece a interação entre o elétron de valência do átomo com o campo
eletromagnético é dada pela expressão (ver apêndice A):
o termo
foi inserido aqui para designar o potencial eletrostático efetivo entre o elétron
de valência e o núcleo e o potencial entre os demais
elétrons.
A expressão (A.11) pode ser simplificada, lembrando que no calibre de Coulomb
. E calculando o termo entre colchetes:
O comutador entre
e
igual a zero significa que a contribuição do produto destes
operadores pode ser somada na equação anterior:
Como:
. Segue que:
.
(4.9)
33
Com este resultado, a relação (4.7) adquire uma nova formulação, mostrada a seguir:
Comparando os valores do terceiro e quarto membros da equação acima. Para determinados
valores de frequência e amplitude da onda incidente, nota-se que
equação (4.2) encontra-se que
. Da
, o que significa que a intensidade da onda
incidente deve ser baixa e oscilar com alta frequência. Ou de forma equivalente,
em que o momento canônico
,
do fóton [4] é dado na última inequação em termos da relação
.
Com estes ajustes, a equação (4.10) é adequadamente reescrita, considerando dois termos
fundamentais: o hamiltoniano íntrinseco ao elétron de valência e adicionalmente o
hamiltoniano que descreve a interação deste com o campo de radiação. Assim,
,
(4.11)
onde
e
4.2.1 – Segunda quantização do termo do elétron
De acordo com o formalismo de segunda quantização [7] a criação e a destruição de uma
partícula na posição
do espaço, são descritas por operadores do tipo
e
, cujas
atribuições estão ligadas, respectivamente a destruição e a criação de uma partícula no estado
m na posição do espaço.
34
Os operadores
e
são lineares e não-hermiteanos, e atuam sobre vetores em
um espaço de Hilbert, denominado de espaço de Fock. Además, estes operadores admitem a
seguinte correspondência:
Onde
é o operador de aniquilação (destruição) de férmions (elétrons) no estado k,
os quais obdecem regras de anti-comutação mostradas no apêndice B pela equação (B.4). Tais
operadores apresentam auto-funções
satisfazendo a relação:
Para reescrever o hamiltoniano de uma partícula
de acordo com o formalismo da segunda
quantização, realiza-se a seguinte combinação:
ℋ
Analogamente, o hamiltoniano do elétron fundamentado na teoria de segunda quantização é
expresso como:
ℋ
Supondo que a base escolhida para expandir
, isto é,
, a equação (4.16) se torna:
ℋ
Lembrando que:
seja a mesma das autofunções de
35
decorre que:
ℋ
Como estamos tratando de um átomo de dois níveis, é natural que o somatório acima sofra
expansão até o segundo termo. Assim
ℋ
No final século XIX, o físico alemão Max Planck sugeriu que a relação entre a energia
proveniente das transições atômicas e a frequência envolvida neste processo é dada da
seguinte forma
[4]. Consequentemente, um átomo de dois níveis estará sujeito
ao seguinte intervalo de energia entre os níveis 1 e 2:
Figura 4.2: Representação da variação de energia para um átomo de dois níveis com frequência de
transição
.
ℋ
Ou simplificadamente (ver apêndice B):
ℋ
36
4.2.2 – Segunda quantização do termo de interação
Assim como foi feito para o campo do elétron, cabe desenvolver neste momento, o
processo de segunda quantização do campo de interação entre o elétron e a radiação incidente,
visando com isso obter a expressão que fornece o hamiltoniano total da interação radiaçãomatéria conforme o modelo semi-clássico.
Os procedimentos matemáticos que permitem obter a quantização do termo de interação
são análogos aos realizados na seção precedente. De modo que:
ℋ
onde
é dado pela expressão (4.12 b). Vale lembrar que o potencial vetor eletromagnético
é dado pela equação (4.2) como:
Substituindo a expressão (4.6) para o campo de radiação monocromático
, encontra-se:
Dessa maneira o hamiltoniano de interação é reescrito a partr de:
ℋ
Perceba que na expressão anterior já fora substituído a expressão para os operadores de
criação
e destruição
, calculados na seção passada.
Em determinadas situações, a integral acima pode ser resolvida analiticamente, caso seja
possível extrair a função trigonométrica ali presente, haja visto que a mesma é escrita em
termos do vetor posição
, que coincide com a variável de integração. Um artifício
amplamente usado neste caso recebe o nome de aproximação de dipolo elétrico. O problema
implica em decompor a distância da posição
do elétron em relação à origem de um eixo de
coordenadas qualquer, considerando agora a posição
aliada a distância
figura 4.3.
do núcleo em relação a essa origem,
do elétron atômico relativo ao seu núcleo. Esta técnica é ilustrada na
37
Figura 4.3: Sistema de eixos coordenados, em que o núcleo atômico dista
raio que o elétron descreve em torno do núcleo. Nesta configuração,
Para observar que
é equivalente ao
fórmula de Euler:
.
, é preciso levar em conta a
, que conduz a:
Fazendo uso da série de Taylor para uma função
Se a função expandida for do tipo
da origem e δ alude ao
, observa-se:
expandida em torno do ponto
,
38
Como
(distância entre o elétron e o núcleo atômico) é da ordem de alguns angstrons e o
comprimento de onda de Broglie
m [8], então o produto
associado ao elétron é aproximadamente igual a
, apontando que os termos entre parênteses que
constam na expressão (4.28) podem ser convenientemente aproximado pela unidade. Logo:
Com isso a expressão (4.26) é reescrita como:
Através da aproximação de dipolo, a função seno torna-se uma constante, e por isso, pode
ser removida para fora da integral, de modo que:
ℋ
Com relação ao operador canônico , o mesmo pode ser expresso em termos do comutador
entre o vetor posição
onde
e o hamiltoniano do elétron. Uma vez que
,
. Dessa relação, segue que:
Assim:
ℋ
Supondo novamente que a base escolhida para expandir
, tal que:
, então:
sejam os autoestados de
39
ℋ
O termo
na equação acima corresponde à própria expressão para
o campo de radiação monocromático (equação 4.6) em que a constante de fase
resultado da contribuição de um deslocamento na onda por um fator igual a
. Já quantidade
é o
, ou seja,
é conhecida na
literatura como dipolo elétrico [9], e resulta da força existente entre duas cargas elétricas
opostas. Portanto,
ℋ
Ou de forma equivalente,
ℋ
Neste ponto, fica claro que em uma transição de dipolo elétrico é preciso que ocorram
transições entre
e
, com
, pois o termo
se anula quando
.
Definindo a frequência de Rabi,
a equação (4.37) é reescrita em função dessa nova grandeza, como:
ℋ
Para um átomo de dois níveis, o somatório acima se desenvolve até o segundo termo. Logo:
40
ℋ
Utilizando o apêncide B.(equação (B.2))
ℋ
tal que:
De posse da equação (4.41), o hamiltoniano que caracteriza a interação entre um campo
de radiação monocromático e um átomo de dois níveis é inteiramente descrito por,
ℋ
4.2.3 – A representação de interação e a aproximação de onda girantes.
A representação de interação é uma técnica que fornece uma nova formulação à E.S., a
partir da aplicação de operadores unitários escrito sob a forma da expressão (3.11 b), como
segue:
em que o hamiltoniano H é tipicamente expresso como:
nela, apenas o termo de interação V contribui para o desenvolvimento temporal do estado, ao
contrário do hamiltoniano livre
que estabelece a energia inerente das partículas envolvidas
no problema.
Aplicando agora a regra da cadeia no lado esquerdo da igualdade (4.43):
41
Utilizando a equação (3.11 b) como o operador unitário
que promove a evolução
temporal do sistema, decorre que:
Portanto, na nova representação tem-se:
tal que a E.S. continua valendo para:
Aplicando estes resultados a equação (4.42), e observando que somente o termo
12 +sen 0 0 −
+ 0 nesta expressão apresenta uma dependência temporal. A
distinção entre o hamiltoniano livre e o termo de interação se processa da seguinte maneira:
e
.
Através destas considerações, o hamiltoniano de interação radiação-matéria na
representação de interação é dado por:
42
Uma alternativa interessante que se utiliza na tentativa de obter uma nova formulação para a
equação precedente consiste na expansão em série de Taylor das exponenciais nela presentes.
Feito isso, o teorema de Hadamard [10] fornece que,
em que
e
são operadores que não comutam entre si.
Com a aplicação do teorema acima na expressão (4.48), e atentando as relações de
comutação mostradas no apêndice B pelas equações (B.5) obtêm-se,
A equação de Euler permite reescrever a função trigonométrica sen
–
em
termos de exponenciais. Valendo-se desta premissa,
É conveniente relembrar que a expressão acima descreve a energia de um átomo de dois
níveis sujeito a um campo de radiação cuja frequencia
é próxima à transição eletrônica
entre os níveis deste átomo. Esta é uma condição peculiar ao regime ressonante ou
aproximadamente ressonante. O cáculo da média temporal é um recurso válido que permite
avaliar quais os termos que colaboram de maneira mais significativa na representação de
interação. Tendo em vista que estes termos em
oscilam com frequências
, logo:
A partir da expressão acima constata-se que a média temporal é claramente superior para os
termos que oscilam com frequência
frequência
, em contraposição daqueles que apresentam
. Estes últimos são geralmente denominados como contra girantes, e são
termos muito oscilantes em média, e portanto, não contribuem consideravelmente para
43
dinâmica do sistema. Este é o mecanismo conhecido como aproximação de ondas girantes
(do inglês Rotating Wave Approximation- RWA) que possibilita reescrever o hamiltoniano de
interação (equação 4.48) da seguinte maneira:
com
Portanto, o hamiltoniano efetivo do modelo átomo-campo conforme as aproximações de
dipolo elétrico e RWA é:
ℋ
Ou na representação de Schr dinger,
ℋ
4.2.4 – Determinação da dinâmica do sistema
No primeiro postulado da mecânica quântica, teve-se a oportunidade de compreender que
um sistema físico isolado pode ser completamente descrito pelo seu vetor de estado. Além
disso, fora abordado na seção 2.1 que qualquer vetor
de base
, onde
, ou alternativamente:
pode ser decomposto em n vetores
Consequentemente, um
átomo de dois níveis pode ser expresso em termos de uma combinação linear dos vetores de
base
:
44
onde
e
são vetores ortogonais e correspondem aos níveis de energia fundamental e
excitado, respectivamente. Também verificou-se que a evolução temporal desse tipo de
sistema é dada pela equação (3.7):
sendo o hamiltoniano efetivo
determinado na tópico anterior pela equação (4.55 b).
Uma tarefa importante que segue desta situação diz respeito à obtenção dos coeficientes
e
em termos dos parâmetros físicos envolvidos no problema. Com isso, toda a
evolução temporal do sistema físico tratado pode ser devidamente conhecida. Para tanto, é
preciso resolver a equação diferencial acima, atentando-se ao fato de que as matrizes
podem ser escritas em função dos estados
e
,
e
como é verificado no apêndice B pelas
expressões (B.4), (B.5) e (B.6).
A solução da expressão (4.57) em função de
e
consiste na solução de equações
diferenciais e requer o estabelecimento de uma série de suposições. Por isso, os detalhes
relativos ao seu cálculo estão organizados na forma de um apêndice (apêndice C), que em
última análise fornece os seguintes resultados:
e
onde:
45
4.3 – Teoria quântica para a descrição da interação radiação-matéria
Neste tópico, far-se-á um estudo envolvendo dois sistemas interagindo entre si, a saber: um
átomo de dois níveis e um campo de radiação monocromático. Porém, ao contrário da seção
precedente, o caráter corpuscular será aplicado ao campo de radiação, o que implica na
quantização dos seus níveis de energia. Dessa maneira, ferramentas matemáticas peculiares à
mecânica quântica serão utilizadas a fim de descrever tal acoplamento.
4.3.1 – Quantização do campo de radiação
Uma aproximação geralmente usada a fim de obter uma solução para
aponta à
suposição de que a onda eletromagnética se propaga sobre condições periódicas de contorno,
como, por exemplo, em uma caixa cúbica de arestas L (ocupando um volume
). Isto
impõe que:
9
Nesta expressão
onda e
é o versor de polarização dado em termos do vetor de propagação
representa a fase do campo. Já as constantes
da
são determinadas substituindo
(4.58) em (4.5), que mostra:
a expressão anterior lembra um oscilador harmônico simples [11], que admite como solução
uma equação periódica do tipo:
Dessa maneira, a energia do campo eletromagnético (no calibre de Coulomb), a nível
clássico, pode ser calculada em função destes parâmetros [12],
9
As iniciais
é uma abreviação geralmente usada para indicar o hermiteano conjugado de uma função de
onda(para maiores detalhes, ver seção 2.5).
46
a qual, por sua vez, é
reduzida aos termos típicos que caracterizam um conjunto de
osciladores harmônicos independentes e desacoplados,
onde
e
são as variáveis canônicas de momentun e posição, respectivamente, com:
e
.
Tais variáveis são agora tratadas como operadores hermiteanos, satisfazendo o postulado
da quantização de Dirac,
61)
Além disso, segundo o princípio de correspondência, considerar-se a equação (4.60 b) como o
operador hamiltoniano do sistema [13].
O formalismo associado aos osciladores harmônicos introduz dois novos operadores, um de
criação e o outro de destruição de fótons, que são expressos em termos de
e
,
estes cumprem a seguinte regra de comutação,
Então, o potencial vetor eletromagnético é expresso, a partir da substituição das relações
(4.62) sobre a expressão (4.58), concedendo,
47
Adicionalmente, o operador hamiltoniano do sistema quantizado é dado inserindo a
equação anterior em (4.60 a) e levando em conta a regra de comutação (4.63),
A equação (4.65) é interpretada como sendo a energia total do campo eletromagnético
quantizado, ou simplesmente, a energia a nível quântico do sistema.
4.3.2 – Hamiltoniano quântico da interação átomo-campo
A abordagem quântica utilizada no estudo de sistemas interagentes pode ser compreeendida
de maneira extensiva ao modelo semi-clássico desenvolvido na seção anterior. De forma
similar, o hamiltoniano que determina a energia total do sistema é atribuído pela energia
particular de cada componente envolvido na interação, isto é,
ℋ
ℋ
ℋ
ℋ
Neste ponto, é necessário lembrar que o hamiltoniano intrínseco do elétron ℋ
já fora
obtido (por meio de técnicas de quantização) pela expressão (4.21). Com relação a energia do
campo de radiação, a equação (4.65) estabelecida segundo a condição de que o campo
eletromagnético satisfaz o postulado de quantização de Dirac, fornece adequadamente o
hamiltoniano do campo incidente ℋ
. Note que este termo não é considerado na teoria
semi-clássica, que trata apenas os níveis eletrônicos do átomo de dois níveis quantizado. No
que tange ao hamiltoniano de interação entre esses dois elementos, a aplicação da equação
(4.12 b) não se justifica mais neste contexto. A melhor maneira de reescrever
é através
48
de (4.64) que considera uma onda com níveis de energia quantizados propagando-se sobre
condições periódicas de contorno. Assim,
que em segunda quantização para o operador
do elétron é dado como:
ℋ
Perceba que em (4.64), o operador
está escrito na representação de Heisenberg,
contudo como um dos intuitos deste estudo é conhecer a dinâmica deste sistema, a equação
(4.68 a) é expressa consoante a representação de Schr dinger, em que o operador é um
parâmetro que não depende do tempo. Por conseguinte, ela é simplicada, a partir de
ℋ
tal que:
ou
49
A transição entre as expressões (4.69 a) e (4.69 b) foi processada realizando novamente a
aproximação de dipolo elétrico. Posteriormente substituiu-se o resultado de (4.33) sobre o
momento canônico
e por fim pressupondo a mesma hipótese feita nas seções 4.2.1 e 4.2.2
na qual a base escolhida para expandir
fora os autoestados de
, tal que:
.
Definindo:
que representa a frequência de Rabi para o caso quântico. Segue de (4.70) que,
onde
Com isso, o hamiltoniano que fornece a energia total do sistema será:
Supondo apenas um modo de vibração ao campo de radiação, a equação anterior é
radicalmente simplificada:
Exprimindo os operadores fermiônicos em função das matrizes de Pauli ou suas
combinações (Apêndice B), e subtraindo o termo
sistema, então:
, que significa a fase global no estado do
50
O hamiltoniano acima é conhecido como Hamiltoniano de Rabi [14], e ainda não possui
solução analítica perante a E.S..
4.3.3 – O modelo de Jaynes-Cummings
O modelo de Jaynes-Cumings (MJC) consiste fundamentalmente no uso das técnicas de
representação de interação e RWA sobre o hamiltoniano de Rabi. Com estas alterações, a
expressão (4.72 c) passa admitir uma solução analítica perante a E.S..
Valendo-se inicialmente da primeira técnica citada; o hamiltoniano livre e o termo de
interação, neste caso, são respectivamente:
.
(4.74)
Com base na equação (4.47), o hamiltoniano de interação é avaliado como,
onde
.
Aplicando novamente o teorema de Hadamard e atentando às relações de comutação
ilustradas no apêndice B, determina-se,
Calculando a média temporal (
, conclui-se que
com incremento
de
que por sua vez, oscila com termos do tipo
. Consequentemente, a contribuição dos termos
se mostram insignificantes em comparação àqueles que oscilam
51
em
termos
. Assim, a aproximação de onda girante implica em desprezar a contribuição dos
e
(contra-girantes) na dinâmica de interação átomo-campo [13].
Dessa forma, no regime de acoplamento fraco (
, onde
é o número médio de
fótons), o hamiltoniano (na representação de Schr dinger) que expressa a interação entre um
átomo de dois níveis e um modo do campo quantizado sobre as aproximações de dipolo e
onda girantes é:
A equação acima recebe o nome de hamiltoniano de Jaynes-Cummings [14]. Ao contrário
de (4.72 c),
é totalmente solúvel perante a E.S..
4.3.4 – Dinâmica do modelo de Jaynes-Cummings
Todo aparato matemático realizado na seção anterior tem como foco principal obter a
dinâmica do sistema estudado. Para tanto, a E.S. (3.7) é utilizada como o mecanismo que
possibilita conhecer a evolução do sistema átomo-campo conforme o modelo de JaynesCummings. Nela, o vetor de estado é expandido na seguinte base de autoestados:
em que
refere-se ao produto tensorial entre o estado eletrônico
campo eletromagnético, tal que
Asssim, a E.S. é escrita da seguinte forma:
. O mesmo se aplica a
e o estado
.
do
52
Neste ponto, cabe observar que o formalismo utilizado para resolver a equação diferencial
de Schr dinger para a interação radiação-matéria via teoria semi-clássica feito na seção 4.2.4
é rigorosamente o mesmo que se apresenta na equação (4.77) que trata o mesmo sistema,
porém, avaliando o campo de radiação com seus níveis quantizados. Evidentemente, os
cálculos realizados na determinação das constantes
e
raciocínio daqueles utilizados no apêndice C, e resultam em
onde:
seguem a mesma linha de
53
Capítulo 5
Resultados e discussões
5.1 – Análise teórica
As funções
e
associadas ao átomo de dois níveis no modelo semi-clássico são
elementos imprescindíveis que quando submetidas as prerrogativas desenvolvidas nos
capítulos 2 e 3 permitem um estudo bastante preciso acerca do átomo. Através delas, é
possível, por exemplo, determinar (em boa aproximação) o comportamento do elétron de
valência atômico. Para tanto, considere que em um instante inicial (
preso ao nível de menor energia, ou seja,
e
) tal elétron esteja
. A aplicação de um campo
de radiação monocromático modifica essa condição, no sentido que a energia dessa fonte é
capturada pelo elétron provocando uma pertubação no átomo. Esta situação é
matematicamente descrita pela equação (4.56), onde
e
foram determinadas por (C
9) e (C 10),
A partir de (5.1) e do postulado 3 da mecânica quântica, mostrado na equação (3.12), a
probabilidade de encontrar o elétron nos estados fundamental e excitado, respectivamente,
após a aplicação do campo será:
e,
54
de modo que a transição deste elétron entre os dois níveis eletrônicos pode ser observada pela
diferença da probabilidade de encontrá-lo nos estados
e
(inversão de população),
Considerando um dos pressupostos do modelo do átomo de dois níveis, a saber, que a
frequência de incidência do campo é ressonante ou aproximadamente ressonante com a
frequência de transição do átomo, isto é,
, e consequentemente
. Segue que:
Conforme o modelo semi-clássico, onde o campo eletromagnético é descrito pelas equações
de Maxwell, o elétron quando excitado por uma fonte externa deve descrever uma trajetória
cíclica entre os níveis eletrônicos do átomo (vide Figura (5.1)), denotando que o mesmo oscila
com a freqüência da radiação entre os níveis atômicos. Sendo possível encontrá-lo, em média,
nos estados excitado e fundamental com a mesma probabiblidade, após realizadas sucessivas
medidas.
Figura 5.1: Gráfico da probabilidade de transição do elétron de valência entre os níveis fundamental e
excitado segundo a teoria semi-clássica.
55
Para uma discussão confrontativa, considere o modelo quântico em que o átomo está
inicialmente no estado excitado e o campo quantizado no vácuo (
. Correspondendo ao
estado inicial,
tal que
e
. Substituindo estes valores nas equações (4.79 a) e
(4.79 b)
para evitar a ocorrência de uma solução trivial (
e
) é preciso que
, ou seja,
Sendo o vetor de estado que caracteriza o sistema escrito como:
De posse de
, o cálculo da inversão de população procede seguindo os mesmos
procedimentos efetuados em (5.2 a) e (5.2 b), mostrando,
56
No regime ressonante,
A equação anterior traduz um resultado supreendente que coloca em conflito a teoria semiclássica e quântica, na tentativa de interpretar o funcionamento do campo de radiação. A
concepção dos “quantum” de energia preconizada pela segunda explica um comportamento
que até então era simplesmente omitido pela física clássica. Isto, porque um campo de
radiação no vácuo no contexto das equações de Maxwell implica em um potencial vetor
eletromagnético nulo, tendo como consequência imediata (conforme indica a equação (4.23))
um campo de radiação com mesmo resultado. Em termos práticos, nenhum evento poderia ser
então observado. Ou em outras palavras, o átomo permaneceria no mesmo estado tanto antes
quanto após a incidência do “campo”. Ao contrário do que estabelece a mecânica quântica,
em que de acordo com a expressão (5.9) pronuncia que o elétron deve experimentar uma
oscilação periódica entre o nível excitado e fundamental.
Uma outra forte evidência da natureza quantizada da luz parte da hipótese de um átomo
inicialmente no estado excitado sendo submetido a uma radiação coerente de amplitude
[14], tal que:
Comparando (5.10) e (4.77), ratifica-se que
e
. O cálculo
das probabilidades de ocupação dos estados excitado e fundamental segue de maneira
inteiramente análoga aos dois casos anteriores. Originando então, a expressão para a inversão
de população deste estado coerente, atribuída por:
57
A Figura 5.2 ilustra o gráfico oriundo da função acima. Nela, observa-se a ocorrência de
oscilações que ora interferem construtivamente ora destrutivamente. Neste último estágio, é
importante notar que a oscilação rigorosamente cessa durante um intervalo de tempo e depois
recomeça com uma amplitude entre os pontos de pico e vale ligeiramente inferior à primeira.
Estas sequências de movimento são tipicamente conhecidas na literatura como colapsos e
revivals e como as amplitudes vão palatinamente diminuindo, o tempo de duração dos
ressurgimentos aumenta na mesma proporção a ponto de se sobreporem. O advento de
colapsos e revivals, só podem ser explicados pelo caráter corpuscular do campo de radiação.
É a natureza quantizada dos seus níveis de energia que ocasiona a oscilação da inversão de
população manifesta pela ação de mínimos e máximos de interferências, dependendo do valor
que
assume na expressão (5.11).
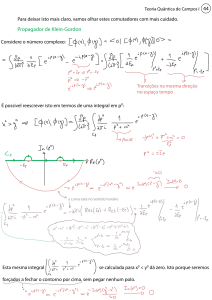
Para reforçar este fato, basta tomar uma contra-prova, isto é, conjecturar que os níveis de
energia do campo de radiação apresentem uma configuração contínua. Com isso, a maneira
mais adequada de representar a inversão de população é através do uso de uma integral sobre
a equação (5.11). Como mostra a Figura 5.3, a função
colapsa, porém não ressurge.
Figura 5.2: Gráfico da inversão de população gerado pela interação do campo de radiação coerente
com um átomo de dois níveis no estado excitado.
58
Figura 5.3: Gráfico da inversão de população supondo que a radiação coerente seja contínua,
obedecendo a expressão
, onde
é chamada
função gama e corresponde ao fatorial de , para números naturais.
5.2 – Um experimento para testar a quantização do campo de radiação.
Durante boa parte do século XX, o MJC se notabilizou por ser uma teoria que trata com
alto grau detalhes e sofisticação a interação entre o átomo e a radiação. No entanto, devido
aos aparatos técnicos que se encontravam ainda em estágio incipiente, a validação
experimental do modelo demandou vários anos para ocorrer satisfatoriamente. Foi apenas em
1996, que o grupo liderado por Serge Haroche, conseguiu utilizar o modelo para demonstrar
de forma adequada os efeitos de quantização do campo de radiação. A Figura 5.4 mostra um
esquema do aparato experimental usado pela equipe na realização dos trabalhos [15].
59
Figura 5.4: Esquema do aparato experimental utilizado por S. Haroche e colaboradores [13].
A Figura acima deve ser analisada a partir do forno O. Nele átomos de rubídio são emitidos
à região de excitação B. A escolha por átomos alcalinos, em particular o rubídio é estratégica.
Analisando sua estrutura eletrônica, verifica-se que ele possui um número quântico muito
elevado, devido a esse fato o elétron de valência passa a maior parte do tempo afastado dos
demais elétrons e do núcleo atômico [17]. Feito este processo, os átomos chegam a cavidade
C, que deve apresentar um alto fator de qualidade [13],
Neste tipo de estrutura,
assume valores próximos a
, haja visto que o tempo de vida
( ) do modo armadillhado dentro da cavidade gira em torno de
modo
e a frequência do
é controlada pela aplicação de uma tensão nos espelhos da cavidade C. O elevado
60
tempo de vida do modo (que proporciona um alto nível de qualidade) aliado ao tempo de vida
do átomo de rubídio (da ordem de
para estados com
), juntos são
consideravelmente superiores ao tempo de interação entre átomo e campo (
) e
constituem uma das premissas fundamentais para a observação do fenômeno.
A frequência de Rabi pode ser obtida pela expressão (4.70), onde o momento de dipolo
do átomo de Rydberg10 é calculado conforme citado na seção (4.2.2) como
o raio atômico médio é dado neste caso por
frequência apresenta uma magnitude de
, sendo
, em que
m. Com isso, a
GHz, o que implica (pela equação (4.71)) em
uma constante de acoplamento ( ) na casa de
Hz. A aplicação de uma tensão mecânica
nos espelhos da cavidade faz com que seus modos se tornem ressonantes (ou
aproximadamente ressonantes) com a transição do átomo de Rydberg.
Por fim, o elétron de valência que apresenta uma baixa energia de ligação com o núcleo é
detectado em D por meio da incidência de ionização seletiva, que se dá pela existência de dois
campos eletrostáticos situados cada um em detectores específicos. O primeiro possui um
campo com dependência temporal e através do controle da velocidade deste feixe é possível
atuar em um estado atômico determinado ionizando-o, uma vez que os níveis eletrônicos do
átomo exibem tempos de ionização característicos. O segundo detector apura todos os elétrons
(independentemente de suas velocidades) do nível atômico selecionado. Para isso, um campo
que varia apenas espacialmente é acoplado a D. A seleção do nível é feita através da
orientação da posição da fenda onde está localizado o elétron multiplicador.
Os gráficos gerados a cerca dos experimentos realizados por Haroche e colaboradores são
mostrados na Figura 5.5. Em (A), observa-se a inversão de população no vácuo. Nesta
configuração, o número médio de fótons
é de 0,06 (±0,01), note que o aspecto do gráfico se
encontra em conformidade com a teoria quântica na descrição do campo de radiação, em que
fóton experimenta oscilações períodicas entre dois níveis eletrônicos. A redução da oscilação
em (A) é devido às fontes de erro inerentes ao experimento, como por exemplo, as contagens
escuras nos detectores por ionização que ocorre devido a lentidão nos fluxos. De forma
complementar a (A), os gráficos (B), (C) e (D) também representam a inversão de população,
a partir da injeção de estados coerentes com 0,40 (±0,02), 0,85 (±0,04) e 1,77 (±0,15) fótons,
10
Por apresentarem propriedades físicas especiais como: elevado número quântico principal e intensa
transição de dipolo elétrica, os átomos de rubídio são também chamados de átomos circulares Rydberg. O
termo circular se justifica devido ao fato assumirem momento angular e
máximos quando excitados por
uma fonte externa.
61
em média, onde o número médio de fótons ( ) é proporcional a
11
. É possível visualisar
em (C) e (D), duas das predições do modelo quântico da luz. Após a primeira oscilação de
ambos os gráficos, a taxa de transferência entre
e , colapsa e ressurge ao longo tempo,
atestando mais uma vez a validade da teoria quântica.
A sequência (a), (b), (c) e (d) surgem a partir da transformada de Fourier sobre os gráficos
supracitados exibindo escalas nas proporções de 4, 3, 1,5 e 1. Eles respondem certamente pela
contribuição mais notável oriunda deste experimento. Por meio deles observar-se picos de
amplitude revelando empiricamente a natureza corpuscular do campo de radiação. Estes picos
são indicados por linhas pontilhadas que possuem os seguintes valores em ordem de
frequência: ,
,
e
, em que
KHz. Progressões como estas do tipo
,
são mais uma evidência do caráter granular da luz, já tendo sido previsto teoricamente neste
texto, quando se abordou a radiação coerente sobre um átomo de dois níveis.
11
Para observar que o número médio de fótons é realmente proporcional a
e
.
, basta calcular
, onde
62
Figura 5.5: De A - D são mostradas as inversões de população considerando os estados iniciais
,
,
,
, respectivamente. De a – d são
mostradas as transformadas de Fourier dos gráficos A – D, respectivamente. As freqüências ,
e
estão indicadas pelas linhas pontilhadas [15].
,
63
Capítulo 6
Conclusões
Por meio de uma revisão literária de conceitos matemáticos que constituem os pilares de
sustentação da mecânica quântica, bem como através das premissas físicas através de seus
postulados, surgiu a oportunidade de desenvolver uma discussão minuciosa envolvendo a
interação entre a radiação eletromagnética monocromática e a matéria. Diversos fenômenos
relevantes sobre o ponto de vista físico foram previstos teoricamente pelo modelo de JaynesCummings, que consiste em uma análise totalmente quântica dos elementos envolvidos na
interação. O advento de colapsos e ressurgimentos a partir da incidência de radiação coerente
sobre a matéria e a ocorrência da emissão espontânea constituem fenômenos explicados
exclusivamente pela consideração de quantização de energia do campo eletromagnético, não
possuindo nenhum análogo na visão da física clássica. De forma ainda mais grave, tais
eventos corroboram a uma noção de incompletude desta última teoria e ascende a mecânica
quântica como um alicerce adequado ao estudo de partículas atômicas.
Uma das provas cabais da quantização da luz foi fornecida por um experimento realizado
pela equipe de Serge Haroche, que constatou que ao atravessar átomos de Rydberg por
cavidades supercondutoras era possível observar o fenômeno dos colapsos e ressurgimentos.
Por intermédio da transformada de Fourier em função do tempo, é possível observar a
existência de freqüências efetivas das inversões de população de fótons que dependiam
diretamente do número quântico , indicando a natureza granular do campo de radiação.
64
7
APÊNDICES
A
Partícula carregada imersa em um campo eletromagnético
Quando uma partícula de massa
se encontra imersa à ação de um campo
eletromagnético, a segunda lei de Newton garante que,
a força com a qual a partícula está sujeita é conhecida como força de Lorentz. Ela surge da
ação de um portador de carga elétrica se movendo em uma região do espaço, e carrega a
contribuição da força elétrica e magnética expressas, respectivamente, como
e
. Logo:
onde os campos elétrico e magnético foram substituídos respectivamente pelas equações (4.2)
e (4.3). Utilizando as seguintes identidades vetoriais:
a equação (A.2) é simplifica como:
A equação (A.4) se assemelha com a relação estabelecida no contexto da mecânica clássica
que conecta a força de um sistema à sua energia potencial, ou matematicamente,
Comparando-a com (A.4), é factível assumir que
.
. Assim é possível obter a
lagrangeana, que por definição é tomada como a diferença entre as energias envolvidas no
problema, tal que:
65
Os formalismos lagrangeano e hamiltoniano estão ligados por [18],
ℋ
em que o momento canônico
é determinado a partir de:
Logo:
ℋ
A energia cinética de um sistema está relacionada à velocidade com que as partículas
pertencentes a este sistema se deslocam, sendo calculada pela expressão
, que
quando implementada em (A.8), reduz a equação a:
ℋ
Efetuando a mesma substiuição no termo entre parêntes de (A.7), que corresponde ao
momento canônico do sistema,
É possível finalmente expressar a hamiltoniana em termos dos parâmetros
ℋ
.
66
B Matrizes de Pauli e suas conexões com operadores de pseudospin e eletrônicos
Uma importante classe de matrizes que será extensivamente usada neste trabalho refere-se
a um conjunto de quatro matrizes de ordem 2 x 2, mostradas na tabela B-1.
Tabela B-1. As matrizes de Pauli. Algumas vezes
referidas como matrizes de Pauli [3].
é omitida da lista, e somente
,
,e
são
Estas matrizes possuem aplicação em vários ramos da física como, por exemplo, momento
angular do spin [19], teoria de grupos, computação quântica, etc.. Elas ainda satisfazem
algumas propriedades que podem facilitar o cálculo de grandezas físicas associadas a tais
matrizes:
;12
1)
2)
;
3)
onde
;
é conhecido como símbolo de Levi-Civita, que pode ser compreendido conforme a
figura B-1.
Figura B-1: Símbolo de Levi-Cevita.
12
O símbolo
é utilizado afim denotar a soma dos elementos da diagonal principal de uma matriz .
67
De acordo com a figura B-1 e com a propriedade 4:
e assim por diante.
Uma outra relação largamente utilizada neste texto remete a equivalência entre operadores
eletrônicos e operadores de Pauli (assim como as matrizes
partir das equações (4.62) que expressam
e
e
). Essa ligação é vista a
, (operadores de criação e destruição do
campo de partículas do campo, sendo conhecidos bósons) em termos das variáveis canônicas
de posição e momentum. Efetuando as relações de anti-comutação13 dos operadores
eletrônicos, que agora são empregados a fim de indicar a produção e aniquilação de elétrons
(férmions), partículas constituintes da matéria que de acordo com o princípio de exclusão de
Pauli não podem ocupar o mesmo estado físico, tem-se que:
com ,
= 1, 2 e fazendo o seguinte mapa:
Obtendo a relação direta destes operadores com àqueles de Pauli:
Como foi abordado na secção 2.4 do presente trabalho, em informação quântica e
computação quântica é comum associar as bases ortonormais
13
Dados dois elementos
e
a vetores na base de
e , a operação de anti-comutação entre eles é definida como:
.
68
um autoestado qualquer, tal que estes vetores14 podem ser representados segundo a seguinte
notação matricial,
e
.
Claramente, combinações do produto interno dos estados desta base podem ser
alternativamente utilizadas em cálculos no qual a aplicação das matrizes de Pauli se mostre
mais favorável15. Abaixo estão listados exemplos da equivalência entre esses dois conceitos:
______________________________________________________________________
______________________________________________________________________
–
Os estados
e
designam ainda os níveis fundamental (
) e excitado (
) do elétron,
respectivamente.
14
Em mecânica quântica, os vetores da base canônica são mais largamente usados para nomear os estados de
spin (momento angular intrínseco) down e up, referentes às bases
e
de uma partícula.
15
No trabalho em questão, matrizes de Pauli foram algumas vezes usadas em substituição dos operadores de
pseudo-spin como, por exemplo, na determinação da dinâmica do sistema tanto para o modelo semi-clássico
quanto para o quântico.
69
C Solução analítica da equação de Schr dinger para o
hamiltoniano radiação-matéria no regime semi-clássico.
A E.S. que dita a evolução temporal do sistema quântico é fornecida pelo segundo
postulado da mecânica quântica (seção 3.2),
O hamiltoniano efetivo de um átomo de dois níveis sujeito a uma radiação externa e o seu
vetor de estado são dados pelas expressões (4.55 b) e (4.56), respectivamente. De modo que, a
E.S. assume o seguinte aspecto quando realizadas estas sustituições:
Derivando temporalmente o vetor de estado no lado esquerdo da equação (C.2):
Já o lado direito de (C.2) é desenvolvido considerando o apêndice B:
Igualando os dois lados da equação:
logo:
70
Fazendo a mudança de variáveis:
Substituindo (C.5 a) e (C.5 b) respectivamente em (C.4 a) e (C.4 b):
Onde:
, dessitonia entre a transição atômica e a frequência do laser (ver figura 4.1).
. Solução da equação (C.6 a):
Supondo uma solução do tipo:
71
Definindo:
Então:
,
ou substituindo na equação (C.5 a) o parâmetro
Os coeficientes
e
são indicados supondo
Fazendo a mesma suposição junto à equação (C.8):
encontrado logo acima, obtém,se:
na expressão (C.4 a). Neste caso,
72
então:
Portanto:
e
Substituindo
e
na equação (C.8), e ainda notando as relações de identidade
trigonométrica decorrentes desta troca, estabelece-se finalmente uma expressão para
em termos da frequência de Rabi
O parâmetro
é obtido realizando o procedimento inteiramente análogo ao feito na
equação (C.6 a), ou de maneira mais simplificada usando
, tendo em
vista que o elétron neste modelo pode ocupar o nível fundamental e excitado, exclusivamente.
Lidando com cada uma dessas possibilidades,
onde
73
REFERENCIAS BIBLIOGRÁFICAS
[1] A. Chaves. Ondas, Relatividade e Física Quântica. Vol. III, 1ª edição. Editora Ernesto
Reichmann, 2007.
[2] A. Steinbruch; P. Winterle. Geometria Analítica. 3ª edição.Makron Books, 1987.
[3] M. A. Nielsen; I. L. Chuang. Computação Quântica e Informação Quântica. Cambridege
University Press (2000).
[4] R. Eisberg e R. Resnick. Física Quântica. 27ª tiragem. Editora Campus, 1979.
[5] M.M. Santos. Proteção de estados coerente em pontos quânticos acoplados. Tese
(Dissertação de mestrado em Física) – Instituto de Física, Universidade Federal de
Uberlândia, Uberlândia. 2011.
[6]S. M. Rezende. Materiais e Dispositivos Eletrônicos. 2ª edição. Livraria da Física, 2004.
[7] D. F. Walls e G. J. Milburn, Quantum Optics, (Springer-Verlag, Berlim, 1995); C. CohenTannoudji, J. Dupont-Roce, G. Grynberg, Photons and Atoms, Introduction to Quantum
Electrodynamics, (Wiley, New York, 1989); Wolfgang P. Schleich, Quantum Optics in Phase
Space, (Wiley-Verlag, Berlim, 2001).
[8]C. Kittel. Introdução a física do estado sólido. 5º edição. Editora Guanabara Dois S.A.,
1978.
[9]D. Hallyday, R. Resnick e K.S Krane. Fundamentos de Física 3.Vol. 3, 5ª edição.Livros
Técnicos e Científicos. Rio de Janeiro, 2004.
[10]W.Miller. Simmetry Groups and their Applications. Academic Press. USA, 1972.
[11] D. Hallyday, R. Resnick e K.S Krane. Fundamentos de Física 2.Vol. 2, 5ª edição.Livros
Técnicos e Científicos. Rio de Janeiro, 2004.
[12] K.D.Machado. Teoria do Eletromagenetismo.Vol. 1.Editora UEPG. Ponta Grossa.
[13]G.G. de Moraes Neto. Engenharia de Hamiltonianos e Aplicação em Teoria da
Informação Quântica. Tese (Dissertação de mestrado em Física– Departamento de Física,
Universidade Federal de São Carlos, São Carlos. 2008.
[14] M.A. Scully e M.S. Zubairy.“Qauntum optics”. Cambridge University Press. USA, 1997.
[15] M. Brune, et. al., Quantum Rabi Oscillation: A Direct Test of Field of Quantization in a
Cavity. Physical Review Letters. Vol. 76, pag. 1800, 1996.
[16] J. M. Raimond, M. Brune, S. Haroche. Rev. Mod. Phys. 565(2001).
74
[17] R. Ejnisman e P. Nussenzveig. Átomos de Rydberg: Estudos Quânticos com “Átomos
Quase Clássicos”. Rev. Brasileira de Ensino de Física. Vol. 19, nº1.São Paulo, 1997.
[18] J. B. Marion e S. T. Thornton. Classical Dynamics of Particles and Systems, 3ª Ed.
Harcourt Brace Jovanovich. Orlando, 1988.
[19]D. J.Griffths. Introduction to quantum mechanics. Second edition. Prentice Hall, 2004.