10 m 6 m Qmin = 0,01 m3/s 10 cm 150 m Bomba ou válvula? 50 m

Mecânica dos Fluidos Ambiental II
Código _____
–
Turma _____
Prof. Maurício Gobbi
–
–
-
Avaliação 2
UFPR
–
029-09-2008
Aluno:
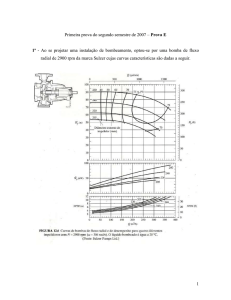
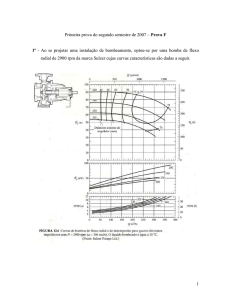
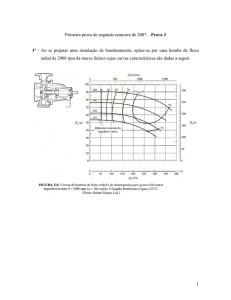
1 Suponha que no sistema hidráulico da figura abaixo necessita-se de uma vazão de, no mínimo, 0, 01 m3 /s.
[20] (a) Descubra se é necessária a presença de uma bomba para manter esta demanda mínima.
[30] (b) Se o sistema precisar de uma bomba, calcule a potência de eixo dessa bomba conhecendo seu coeficiente de vazão de
5, seu coeficiente de potência (eixo) de 0,6 e seu coeficiente de carga de 0.096. Se o sistema não precisar da bomba (se sobrar
energia/vazão), calcule a perda de carga necessária para levar a vazão para o exato valor de 0, 01 m3 /s, perda de carga esta que
seria implantada colocando-se uma válvula no lugar da bomba (ver figura).
[10] (c) Suponha agora que, por uma grave falha, a bomba (ou válvula) reduz repentinamente o fluxo de água para a metade da
vazão normal. Uma onda de pressão se formará. Calcule a velocidade da onda de pressão.
[20] (d) Calcule a amplitude da onda de pressão (o aumento/redução de pressão) em Pa e em unidade de altura de coluna d’água
(se você não fez o ítem (c) use vel. da onda de 1400 m/s).
Considere para os ítens acima tubo perfeitamente liso, perdas de carga localizadas com quinas vivas (K = 0,5 e K = 1 no
reservatório da esquerda e direita, respectivamente), densidade da água 988 kg/m3 , viscosidade 0,00055 kg/ms, módulo de
elasticidade da água 2,5 × 109 Pa.
150 m
10 m
50 m
10 cm
Bomba ou
válvula?
6m
Qmin = 0, 01 m3 /s
Figura 1: Sistema de abastecimento.
SOLUÇÃO:
Equação de Bernoulli entre as superfícies, onde V1 = V2 ≈ 0 e p1 = p2 = patm :
V2
L
z1 = z2 +
f + K1 + K2 + H.
2g
D
Se H der negativo, precisamos de bomba, se der positivo, precisamos de válvula. Usando os dados do problema lembrando que
a velocidade V = 1,27 m/s no tubo é a vazão dada sobre a área, e o fator de atrito é obtido entrando na formula de Moody
diretamente com Re = 2,3 × 105 , e tubo liso, temos f = 0,015e então:
H = 10 − 6 − 123 × 0,015 + 0,123 ≈ 2 m
2
Portanto, precisamos de uma válvula com perda de carga de 2 m, ou K = 2/ V2g (ítens a e b).
Ao fecharmos
a válvula para velocidade V /2 = 1,27/2 cria-se uma onda de pressão, cuja velocidade pode ser calculada como
p
a = k/ρ = 1591 m/s (ítem c).
A onda de pressão causa um aumento da pressão dado por:
1,27
∆p = −ρa∆V = −998 × 1591 × −
≈ 1 × 106 Pa
2
Em termos de altura de coluna água: ∆h =
∆p
ρg
= 103 m (ítem d).
2 [20] O software EPANET possui no seu bojo, várias coisas que estudamos no nosso curso. Entre elas, o software calcula a perda
de carga distribuída nos condutos com a fórmula hl = Aq B , onde q é a vazão e A e B são dadas na figura abaixo. Entretanto, o
EPANET dá 3 opções (praticamente equivalentes) de formulação do cálculo de perda de carga. Veja a figura abaixo. Identifique
qual dos 3 é o método mais próximo do que nós usamos no nosso curso, e identifique as diferenças (se houver). Seja sucinto: quero
a resposta em 3-5 linhas no máximo.
Figura 2: Pedacinho do manual EPANET-Brasil.
SOLUÇÃO:
A fórmula dada no curso é a de Darcy-Weisbach, que, no manual do EPANET aparece em termos da vazão Q em vez de velocidade
2
V , e onde a constante 1/2g foi absorvida na constante 0,0827. Lembrando que Q = V πd4 , e que o parâmetro f continua sendo
função do número de Reynolds e da rugosidade, já que Re é função de q e d (além da viscosidade e densidade da água, que não
aparecem por serem aproximadamente constantes).