BIOPOTENCIAL 1. Potencial de Repouso Prof. Sérgio Francisco

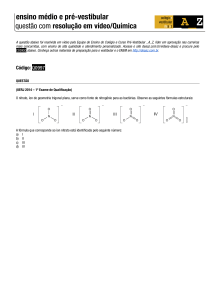
BIOPOTENCIAL
1.
Potencial de Repouso
Prof. Sérgio Francisco Pichorim
Fig. 2.2. Cortical nerve cell and nerve endings connected to it.
Fig. 2.3. A sketch illustrating how the phospholipid molecules behave in water. The cell
is enclosed by a cell membrane whose thickness is about 7.5 - 10 nm. It consists of
phosphoric acid and fatty acids called glycerides. The head of this molecule is
hydrophilic (attracted to water). The fatty acids have tails consisting of hydrocarbon
chains which are hydrophobic (repelled by water). .
Fig. 2.4. The construction of a cell membrane. The main constituents are two lipid
layers, with the hydrophobic tails pointing inside the membrane. The macromolecular
pores in the cell membrane form the ionic channels through which sodium, potassium,
and chloride molecules flow through the membrane and generate the bioelectric
phenomena.
POTENCIAL DE REPOUSO
MICROELETRODO
Micropipeta
CONCENTRAÇÕES IÔNICAS INTRA E EXTRACELULAR
EXEMPLO 1
Exemplo 2 – Célula Muscular
Concentrações
em mMol/l
Intracelular
Extracelular
Na+
12
145
K+
155
4
Cl-
4
120
BOMBA SÓDIO-POTÁSSIO
• Seqüência de reações químicas (cf. Okuno)
• Exemplo didático
• Outro
exemplo
didático
Determinação da Tensão de
Membrana (Vm)
• Tensão através de membrana com diferença
de concentrações.
VOLTÍMETRO
Movimento Browniano (Einstein, 1905)
• Real, em Vídeo e Simulação matemática
• Energia Térmica = Energia Cinética
• Coeficiente de Difusão de uma partícula (D)
• Mobilidade do Íon (µ)
Equação de NERNST
• Relação de EINSTEIN
D / µ = k.T / q
• Equilíbrio de DONNAN
Jc + Je = 0
Equação de NERNST
• Lei de FICK
• Lei de OHM
Equação de NERNST
• R = Cte Universal dos Gases 8,3144 J/K/mol
• F = Constante de Faraday 96.485,3 C/mol
• z = valência do íon
Exercício – Calcular a Tensão de Nernst para
cada íon da célula muscular (rã a 16oC)
Concentração
em mMol/l
K+
Na+
Ca++
Mg++
ClHCO3-
Extracelular
Intracelular
2,25
124
109
10,4
2,1
4,9
1,25
14
77,5
1,5
26,6
12,4
Tensão de
NERNST (mV)
Potencial de Repouso (Vm) é de – 98 mV.
Equação de Goldman-Hodgkin-Katz (1943-1949)
• Exemplo: Axônio de Lula Gigante tem as
permeabilidades com a seguinte relação:
PK:PNa:PCl = 1:0,03:0,1 ou seja, Vm =
• Durante um Potencial de Ação esta relação
muda para:
PK:PNa:PCl =1:15:0,1 ou seja, Vm =
• Modelo elétrico para o Potencial de Repouso
• Cálculo da Tensão de Membrana (Vm)