Aula P7

http://eo.tagus.ist.utl.pt/
LEI de FARADAY
ε = −B av
ε = − dΦdt
0
F = B0 Ia
r r
d r r
∫ E ⋅ dr = − dt ∫ B ⋅ dS
Γ
S
25-10-2010
http://web.tagus.ist.utl.pt/~mircea.rogalski/
Aula P7: Lei de Faraday
1
http://eo.tagus.ist.utl.pt/
R 0 = 1Ω/m
Um fio condutor com abertura angular 2α= 60º está colocado num
campo magnético B perpendicular ao seu plano. Uma vara condutora desliza com velocidade de
translação constante v, mantendo o contacto eléctrico com o fio. Sabendo que os três ramos do circuito
eléctrico têm a mesma resistência R0 por unidade de comprimento:
(i) Determine a expressão datensão e induzida no circuito;
(ii) Mostre que a intensidade da corrente induzida se mantém constante.
α
v
α
(i)
B
ε = (2Bv2tgα)t
(ii)
25-10-2010
Aula P7: Lei de Faraday
2
http://eo.tagus.ist.utl.pt/
Uma vara de comprimento L roda em torno do centro duma espira
circular, com velocidade angular constante w, sob acção de uma força F. Sabendo que o circuito
fechado, cuja resistência eléctrica total tem o valor R, se encontra num campo magnético uniforme B,
perpendicular ao seu plano, determine:
(i) A tensão induzida no circuito;
(ii) A força F necessária para que o movimento de rotação se mantenha uniforme .
F
B
L
R
(i)
ε = BL ω/2
(ii)
F = B2L3ω/4R
2
25-10-2010
Aula P7: Lei de Faraday
3
http://eo.tagus.ist.utl.pt/
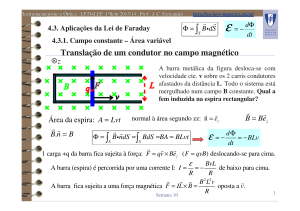
Uma espira condutora rectangular, com massa m, arestas a e h>>a e
resistência R é largada no campo gravítico e desloca-se no plano vertical da figura. O campo magnético
uniforme de indução B é perpendicular ao plano vertical.
(i) Obtenha a expressão da força electromotriz ε induzida pelo movimento vertical em função da
velocidade v de queda e a expressão da força magnética F que actua na espira condutora.
(ii) Admitindo que o movimento se torna praticamente uniforme antes da aresta superior da espira
entrar no campo magnético, determine a velocidade limite vlim de queda, a partir da equação do
movimento vertical.
(iii) Obtenha a expressão da velocidade de queda em função do tempo e justifique a aproximação
considerada no ponto anterior.
a
h
F
v
mg
B
(i)
ε = Bav
(ii) F = B2a2v/R
(iii) v = mgR/B2a2
lim
25-10-2010
(iv)
Aula P7: Lei de Faraday
4
http://eo.tagus.ist.utl.pt/
Um quadro metálico de secção quadrada com aresta a, resistência
eléctrica R e massa m está em queda livre no plano vertical. Sabendo que o campo magnético
transversal (horizontal) representado na figura aumenta a partir do chão conforme:
B(z) = B0 + kz
onde z representa a altura, B0 e k são constantes.
Determine a velocidade limite da queda livre do quadro.
z + a
x B
z
g
25-10-2010
Aula P7: Lei de Faraday
5
http://eo.tagus.ist.utl.pt/
Uma haste metálica, com massa m e comprimento l, desliza sem atrito
no campo gravítico, sempre em contacto com duas varas verticais, ligadas por um condensador de
capacidade C. Sabendo a indução magnética B perpendicular ao plano vertical, e negligenciando a
resistência eléctrica do circuito, determine:
(i) a força electromotriz ε induzida pelo movimento vertical e a carga Q do condensador em função
da velocidade de queda.
(ii) a corrente de carga do condensador e a força magnética F que actua na haste.
(iii) a aceleração de queda da haste.
C
B
F
mg
l
(i)
ε = Blv
(ii) I = CBla
Q = CBlv
F = CB2l2a
(iii)
25-10-2010
Aula P7: Lei de Faraday
6
http://eo.tagus.ist.utl.pt/
Uma haste metálica, de massa m e comprimento l desliza sem atrito
no campo gravítico, sempre em contacto com duas varas verticais, ligadas por uma bobina de
indutância L. Sabendo a indução magnética B perpendicular ao plano vertical, e negligenciando a
resistência eléctrica do circuito, determine:
(i) A intensidade da corrente no circuito
(ii) A força magnética
(iii) O período de oscilação vertical da haste.
L
B
x
mg
l
(i)
I = (Bl/L)x
(ii) F = (B2l2/L)x
(iii)
25-10-2010
Aula P7: Lei de Faraday
7