Física Vestibular - FUVEST

Física
Vestibular - FUVEST
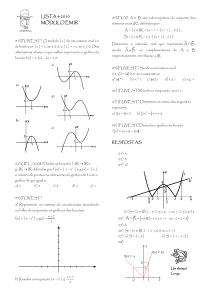
1. (Fuvest 2014) Um corpo de massa M desliza sem atrito, sujeito a uma força gravitacional
vertical uniforme, sobre um “escorregador logarítmico”: suas coordenadas (x, y) no plano
cartesiano, que representam distâncias medidas em metros, pertencem ao gráfico da função
f(x)  log 1 x  4.
2
O corpo começa sua trajetória, em repouso, no ponto A, de abscissa x  1, e atinge o chão no
ponto B, de ordenada y  0, conforme figura abaixo.
Não levando em conta as dimensões do corpo e adotando 10m/s2 como o valor da aceleração
da gravidade,
a) encontre a abscissa do ponto B;
b) escreva uma expressão para a energia mecânica do corpo em termos de sua massa M, de
sua altura y e de sua velocidade escalar v;
c) obtenha a velocidade escalar v como função da abscissa do ponto ocupado pelo corpo;
d) encontre a abscissa do ponto a partir do qual v é maior do que
60 m / s.
2. (Fuvest 2015) O sistema de airbag de um carro é formado por um sensor que detecta
rápidas diminuições de velocidade, uma bolsa inflável e um dispositivo contendo azida de sódio
(NaN3 ) e outras substâncias secundárias. O sensor, ao detectar uma grande desaceleração,
produz uma descarga elétrica que provoca o aquecimento e a decomposição da azida de
sódio. O nitrogênio (N2 ) liberado na reação infla rapidamente a bolsa, que, então, protege o
motorista. Considere a situação em que o carro, inicialmente a 36 km / h (10 m / s), dirigido por
um motorista de 60 kg, para devido a uma colisão frontal.
a) Nessa colisão, qual é a variação ΔE da energia cinética do motorista?
b) Durante o 0,2 s da interação do motorista com a bolsa, qual é o módulo α da aceleração
média desse motorista?
c) Escreva a reação química de decomposição da azida de sódio formando sódio metálico e
nitrogênio gasoso.
d) Sob pressão atmosférica de 1atm e temperatura de 27 C, qual é o volume V de gás
nitrogênio formado pela decomposição de 65 g de azida de sódio?
1
Note e adote:
Desconsidere o intervalo de tempo para a bolsa inflar;
Ao término da interação com a bolsa do airbag, o motorista está em repouso;
Considere o nitrogênio como um gás ideal;
Constante universal dos gases: R  0,08 atm / (mol K);
0 C  273 K.
Elemento
sódio
nitrogênio
Massa atômica (g / mol)
23
14
3. (Fuvest 2013) Antes do início dos Jogos Olímpicos de 2012, que aconteceram em Londres,
a chama olímpica percorreu todo o Reino Unido, pelas mãos de cerca de 8000 pessoas, que se
revezaram nessa tarefa. Cada pessoa correu durante um determinado tempo e transferiu a
chama de sua tocha para a do próximo participante.
Suponha que
(i) cada pessoa tenha recebido uma tocha contendo cerca de 1,02 g de uma mistura de butano
e propano, em igual proporção, em mols;
(ii) a vazão de gás de cada tocha fosse de 48 mL/minuto.
Calcule:
a) a quantidade de matéria, em mols, da mistura butano+propano contida em cada tocha;
b) o tempo durante o qual a chama de cada tocha podia ficar acesa.
Um determinado participante P do revezamento correu a uma velocidade média de 2,5 m/s.
Sua tocha se apagou no exato instante em que a chama foi transferida para a tocha do
participante que o sucedeu.
c) Calcule a distância, em metros, percorrida pelo participante P enquanto a chama de sua
tocha permaneceu acesa.
Dados: Massa molar (g/mol): butano = 58, propano = 44; Volume molar nas condições
ambientes: 24 L/mol.
4. (Fuvest 2015) Uma criança com uma bola nas mãos está sentada em um “gira‐gira” que
roda com velocidade angular constante e frequência f  0,25 Hz.
a) Considerando que a distância da bola ao centro do “gira‐gira” é 2 m, determine os módulos
da velocidade VT e da aceleração a da bola, em relação ao chão.
Num certo instante, a criança arremessa a bola horizontalmente em direção ao centro do
“gira‐gira”, com velocidade VR de módulo 4 m / s, em relação a si.
Determine, para um instante imediatamente após o lançamento,
b) o módulo da velocidade U da bola em relação ao chão;
c) o ângulo θ entre as direções das velocidades U e VR da bola.
Note e adote:
π3
2
5. (Fuvest 2015) Uma criança de 30 kg está em repouso no topo de um escorregador plano
de 2,5 m 2,5 m de altura, inclinado 30 em relação ao chão horizontal. Num certo instante, ela
começa a deslizar e percorre todo o escorregador.
Determine
a) a energia cinética E e o módulo Q da quantidade de movimento da criança, na metade do
percurso;
b) o módulo F da força de contato entre a criança e o escorregador;
c) o módulo a da aceleração da criança.
Note e adote:
Forças dissipativas devem ser ignoradas.
A aceleração local da gravidade é 10 m / s2.
sen 30  cos 60  0,5
sen 60  cos 30  0,9
6. (Fuvest 2015) A energia necessária para o funcionamento adequado do corpo humano é
obtida a partir de reações químicas de oxidação de substâncias provenientes da alimentação,
que produzem aproximadamente 5 kcal por litro de O2 consumido. Durante uma corrida, um
atleta consumiu 3 litros de O2 por minuto.
Determine
a) a potência P gerada pelo consumo de oxigênio durante a corrida;
b) a quantidade de energia E gerada pelo consumo de oxigênio durante 20 minutos da
corrida;
c) o volume V de oxigênio consumido por minuto se o atleta estivesse em repouso,
considerando que a sua taxa de metabolismo basal é 100 W.
Note e adote:
1cal  4 J.
7. (Fuvest 2015) O espelho principal de um dos maiores telescópios refletores do mundo,
localizado nas Ilhas Canárias, tem 10 m de diâmetro e distância focal de 15 m. Supondo que,
inadvertidamente, o espelho seja apontado diretamente para o Sol, determine:
a) o diâmetro D da imagem do Sol;
b) a densidade S de potência no plano da imagem, em W / m2 ;
c) a variação ΔT da temperatura de um disco de alumínio de massa 0,6 kg colocado no plano
da imagem, considerando que ele tenha absorvido toda a energia incidente durante 4 s.
Note e adote:
π3
O espelho deve ser considerado esférico.
Distância Terra  Sol  1,5  1011 m.
Diâmetro do Sol  1,5  109 m.
Calor específico do Al  1J / (g K). Calor específico do Al = 1 J/(g K).
Densidade de potência solar incidindo sobre o espelho principal do telescópio  1kW / m2.
O diâmetro do disco de alumínio é igual ao da imagem do Sol.
Desconsidere perdas de calor pelo disco de alumínio.
3
8. (Fuvest 2015) Um recipiente hermeticamente fechado e termicamente isolado, com volume
de 750 , contém ar inicialmente à pressão atmosférica de 1atm 1 atm e à temperatura de
27C. No interior do recipiente, foi colocada uma pequena vela acesa, de 2,5 g. Sabendo‐se
que a massa da vela é consumida a uma taxa de 0,1g / min e que a queima da vela produz
energia à razão de 3,6  104 J / g, determine
a) a potência W da vela acesa;
b) a quantidade de energia E produzida pela queima completa da vela;
c) o aumento ΔT da temperatura do ar no interior do recipiente, durante a queima da vela;
d) a pressão P do ar no interior do recipiente, logo após a queima da vela.
Note e adote:
O ar deve ser tratado como gás ideal.
O volume de 1mol de gás ideal à pressão atmosférica de 1atm e à temperatura de 27C é
25 .
Calor molar do ar a volume constante: Cv  30 J /  mol K  .
Constante universal dos gases: R  1,08 atm / mol K  .
0C  273 K. 0 °C = 273 K.
Devem ser desconsideradas a capacidade térmica do recipiente e a variação da massa de gás
no seu interior devido à queima da vela.
9. (Fuvest 2015) A região entre duas placas metálicas, planas e paralelas está esquematizada
na figura abaixo. As linhas tracejadas representam o campo elétrico uniforme existente entre as
placas. A distância entre as placas é 5 mm e a diferença de potencial entre elas é 300 V. As
coordenadas dos pontos A, B e C são mostradas na figura. Determine
a) os módulos EA , EB e EC do campo elétrico nos pontos A, B e C, respectivamente;
b) as diferenças de potencial VAB e VBC entre os pontos A e B e entre os pontos B e C,
respectivamente;
c) o trabalho τ realizado pela força elétrica sobre um elétron que se desloca do ponto C ao
ponto A.
Note e adote:
O sistema está em vácuo.
Carga do elétron  1,6  1019 C.
4
10. (Fuvest 2015) O aquecimento de um forno elétrico é baseado na conversão de energia
elétrica em energia térmica em um resistor. A resistência R do resistor desse forno, submetido
a uma diferença de potencial V constante, varia com a sua temperatura T. Na a seguir é
mostrado o gráfico da função R(T)  R0  α(T  T0 ), sendo R0 o valor da resistência na
temperatura T0 e α uma constante.
Ao se ligar o forno, com o resistor a 20C, a corrente é 10 A. Ao atingir a temperatura TM, a
corrente é 5 A.
Determine a
a) constante α;
b) diferença de potencial V;
c) temperatura TM;
d) potência P dissipada no resistor na temperatura TM.
11. (Fuvest 2014) A primeira medida da velocidade da luz, sem o uso de métodos
astronômicos, foi realizada por Hippolyte Fizeau, em 1849. A figura abaixo mostra um esquema
simplificado da montagem experimental por ele utilizada.
Um feixe fino de luz, emitido pela fonte F, incide no espelho plano semitransparente E 1. A luz
refletida por E1 passa entre dois dentes da roda dentada R, incide perpendicularmente no
espelho plano E2 que está a uma distância L da roda, é refletida e chega ao olho do
observador. A roda é então colocada a girar em uma velocidade angular tal que a luz que
atravessa o espaço entre dois dentes da roda e é refletida pelo espelho E 2, não alcance o olho
do observador, por atingir o dente seguinte da roda. Nesta condição, a roda, com N dentes,
gira com velocidade angular constante e dá V voltas por segundo.
a) Escreva a expressão literal para o intervalo de tempo Δt em que a luz se desloca da roda
até E2 e retorna à roda, em função de L e da velocidade da luz c.
5
b) Considerando o movimento de rotação da roda, escreva, em função de N e V, a expressão
literal para o intervalo de tempo Δt decorrido entre o instante em que a luz passa pelo ponto
central entre os dentes A e B da roda e o instante em que, depois de refletida por E 2, é
bloqueada no centro do dente B.
c) Determine o valor numérico da velocidade da luz, utilizando os dados abaixo.
Note e adote:
No experimento de Fizeau, os dentes da roda estão igualmente espaçados e têm a mesma
largura dos espaços vazios;
L = 8600 m;
N = 750;
V = 12 voltas por segundo.
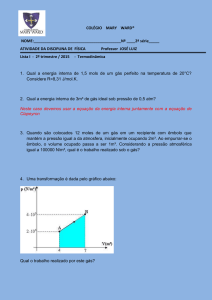
12. (Fuvest 2014) Arnaldo e Batista disputam uma corrida de longa distância. O gráfico das
velocidades dos dois atletas, no primeiro minuto da corrida, é mostrado na figura.
Determine
a) a aceleração aB de Batista em t = 10 s;
b) as distâncias dA e dB percorridas por Arnaldo e Batista, respectivamente, até t = 50 s;
c) a velocidade média v A de Arnaldo no intervalo de tempo entre 0 e 50 s.
13. (Fuvest 2014) Duas pequenas esferas, cada uma com massa de 0,2 kg, estão presas nas
extremidades de uma haste rígida, de 10 cm de comprimento, cujo ponto médio está fixo no
eixo de um motor que fornece 4 W de potência mecânica. A figura abaixo ilustra o sistema.
No instante t = 0, o motor é ligado e o sistema, inicialmente em repouso, passa a girar em torno
do eixo. Determine
a) a energia cinética total E das esferas em t = 5 s;
b) a velocidade angular ω de cada esfera em t = 5 s;
c) a intensidade F da força entre cada esfera e a haste, em t = 5 s;
d) a aceleração angular média α de cada esfera, entre t = 0 e t = 5 s.
Note e adote:
6
As massas da haste e do eixo do motor devem ser ignoradas.
Não atuam forças dissipativas no sistema.
14. (Fuvest 2014) Há um ponto no segmento de reta unindo o Sol à Terra, denominado “Ponto
de Lagrange L1”. Um satélite artificial colocado nesse ponto, em órbita ao redor do Sol,
permanecerá sempre na mesma posição relativa entre o Sol e a Terra.
Nessa situação, ilustrada na figura acima, a velocidade angular orbital ωA do satélite em torno
do Sol será igual à da Terra, ωT .
Para essa condição, determine
a) ωT em função da constante gravitacional G, da massa MS do Sol e da distância R entre a
Terra e o Sol;
b) o valor de ωA em rad/s;
c) a expressão do módulo Fr da força gravitacional resultante que age sobre o satélite, em
função de G, MS ,MT, m, R e d, sendo MT e m, respectivamente, as massas da Terra e do
satélite e d a distância entre a Terra e o satélite.
Note e adote:
1ano  3,14  107 s.
O módulo da força gravitacional F entre dois corpos de massas M1 e M2, sendo r a distância
entre eles, é dado por F = G M1 M2/r2.
Considere as órbitas circulares.
15. (Fuvest 2014) Um contêiner com equipamentos científicos é mantido em uma estação de
pesquisa na Antártida. Ele é feito com material de boa isolação térmica e é possível, com um
pequeno aquecedor elétrico, manter sua temperatura interna constante, Ti  20C, quando a
temperatura externa é Te  40C. As paredes, o piso e o teto do contêiner têm a mesma
espessura, ε  26 cm, e são de um mesmo material, de condutividade térmica
k  0,05 J / (s  m  C). Suas dimensões internas são 2  3  4 m3 . Para essas condições,
determine
a) a área A da superfície interna total do contêiner;
b) a potência P do aquecedor, considerando ser ele a única fonte de calor;
c) a energia E, em kWh, consumida pelo aquecedor em um dia.
Note e adote:
A quantidade de calor por unidade de tempo (Φ) que flui através de um material de área A,
espessura ε e condutividade térmica k, com diferença de temperatura ΔT entre as faces
do material, é dada por: Φ  kAΔT / ε.
16. (Fuvest 2014) Uma pessoa faz, diariamente, uma caminhada de 6 km em uma pista
horizontal, consumindo 80 cal a cada metro. Num certo dia, ela fez sua caminhada habitual e,
7
além disso, subiu um morro de 300 m de altura. Essa pessoa faz uma alimentação diária de
2000 kcal, com a qual manteria seu peso, se não fizesse exercícios.
Com base nessas informações, determine
a) a percentagem P da energia química proveniente dos alimentos ingeridos em um dia por
essa pessoa, equivalente à energia consumida na caminhada de 6 km;
b) a quantidade C de calorias equivalente à variação de energia potencial dessa pessoa entre a
base e o topo do morro, se sua massa for 80 kg;
c) o número N de caminhadas de 6 km que essa pessoa precisa fazer para perder 2,4 kg de
gordura, se mantiver a dieta diária de 2000 kcal.
Note e adote:
A aceleração da gravidade local é igual a 10 m/s2.
1 cal = 4 J.
9 kcal são produzidas com a queima de 1 g de gordura.
17. (Fuvest 2014) A curva característica de uma lâmpada do tipo led (diodo emissor de luz) é
mostrada no gráfico.
Essa lâmpada e um resistor de resistência R estão ligados em série a uma bateria de 4,5 V,
como representado na figura abaixo.
Nessa condição, a tensão na lâmpada é 2,5 V.
a) Qual é o valor da corrente iR no resistor?
b) Determine o valor da resistência R.
c) A bateria de 4,5 V é substituída por outra de 3 V, que fornece 60 mW de potência ao circuito,
sem que sejam trocados a lâmpada e o resistor. Nessas condições, qual é a potência PR
dissipada no resistor?
Note e adote:
As resistências internas das baterias devem ser ignoradas.
8
18. (Fuvest 2013) Um DJ, ao preparar seu equipamento, esquece uma caixa de fósforos sobre
o disco de vinil, em um toca-discos desligado. A caixa se encontra a 10 cm do centro do disco.
Quando o toca-discos é ligado, no instante t  0, ele passa a girar com aceleração angular
constante α  1,1rad/s2 , até que o disco atinja a frequência final f  33 rpm que permanece
constante. O coeficiente de atrito estático entre a caixa de fósforos e o disco é μe  0,09.
Determine
a) a velocidade angular final do disco, ωf , em rad/s;
b) o instante tf em que o disco atinge a velocidade angular ωf ;
c) a velocidade angular ωc do disco no instante tc em que a caixa de fósforos passa a se
deslocar em relação ao mesmo;
d) o ângulo total θ percorrido pela caixa de fósforos desde o instante t  0 até o instante
t  tc .
Note e adote: Aceleração da gravidade local g  10 m/s2; π  3.
19. (Fuvest 2013) A potência elétrica instalada no Brasil é 100 GW. Considerando que o
equivalente energético do petróleo seja igual a 4  107 J/L, que a potência média de radiação
solar por unidade de área incidente na superfície terrestre seja igual a 250 W/m 2 e que a
relação de equivalência entre massa m e energia E é expressa por E  mc 2 , determine
a) a área A de superfície terrestre, na qual incide uma potência média de radiação solar
equivalente à potência elétrica instalada no Brasil;
b) a energia elétrica EB consumida no Brasil em um ano, supondo que, em média, 80% da
potência instalada seja utilizada;
c) o volume V de petróleo equivalente à energia elétrica consumida no Brasil em um ano;
d) a massa m equivalente à energia elétrica consumida no Brasil em um ano.
Note e adote: 1GW  109 W; c  3  108 m/s; 1 ano = 3  107 s.
20. (Fuvest 2013) Uma das hipóteses para explicar a extinção dos dinossauros, ocorrida há
cerca de 60 milhões de anos, foi a colisão de um grande meteoro com a Terra. Estimativas
indicam que o meteoro tinha massa igual a 1016 kg e velocidade de 30 km/s, imediatamente
antes da colisão. Supondo que esse meteoro estivesse se aproximando da Terra, numa
direção radial em relação à orbita desse planeta em torno do Sol, para uma colisão frontal,
determine
a) a quantidade de movimento Pi do meteoro imediatamente antes da colisão;
b) a energia cinética Ec do meteoro imediatamente antes da colisão;
c) a componente radial da velocidade da Terra, Vr, pouco depois da colisão;
d) a energia Ed, em megatons, dissipada na colisão.
Note e adote: A órbita da Terra é circular; Massa da Terra = 6  1024 kg; 1 megaton =
4  1015 J é a energia liberada pela explosão de um milhão de toneladas de trinitrotolueno.
21. (Fuvest 2013) Em uma aula de laboratório, os alunos determinaram a força eletromotriz ε e
a resistência interna r de uma bateria. Para realizar a tarefa, montaram o circuito representado
na figura abaixo e, utilizando o voltímetro, mediram a diferença de potencial V para diferentes
valores da resistência R do reostato. A partir dos resultados obtidos, calcularam a corrente I no
reostato e construíram a tabela apresentada logo abaixo.
9
a) Complete a tabela abaixo com os valores da corrente I.
V(V)
1,14
1,10
1,05
0,96
0,85
R(  )
7,55
4,40
2,62
1,60
0,94
I(A)
0,15
0,40
0,90
b) Utilizando os eixos abaixo, faça o gráfico de V em função de I.
c) Determine a força eletromotriz ε e a resistência interna r da bateria.
Note e adote: Um reostato é um resistor de resistência variável; Ignore efeitos resistivos dos
fios de ligação do circuito.
10
Gabarito:
Resposta da questão 1:
a) Quando x  xB  yB  0.
Assim:
log 1 x  4  0  log 1 x  4 
2
2
 1
2
 
4
 x  x  24

x  16 unidades de comprimento.
b) Usando a expressão da Energia Mecânica:
Emec  Ecin  Epot
 Emec 
 v2

M v2
 M g y  Emec  M 
 g y
 2

2



 v2

Emec  M 
 10 y  unidades de energia.
 2



c) Como o corpo parte do repouso em x = 1, temos v0 = 0.
Na expressão dada, para x = 1, temos:
y  log 1 1  4  0  4  y  4.
2
Aplicando esses dados na expressão obtida no anterior:
 v2

 02

Emec  M 
 10 y   Emec  M 
 10  4  
 2

 2





Emec  40 M .
Pela conservação da Energia Mecânica:
 2


v
v2
v2
M
 10  log 1 x  4    40 M 
 40  10 log 1 x  40 
 -10 log 1 x 
 2


2
2
2
2
2




v
-20 log 1 x .
2
Caso queiramos eliminar o sinal (–) do radicando, podemos mudar o logaritmo para a base
2:
log2 x log2 x
log 1 x 

 log 1 x  log2 x.
1
1
log2
2
2
2
Assim:
v
20 log2 x unidades de velocidade.
Resposta da questão 2:
[Resposta do ponto de vista da disciplina de Física]
Dados: m  60 kg; v  0; v0  10 m/s; Δt  0,2 s.
a) A variação da energia cinética (ΔE) é:
11
ΔE  E  E0 



m 2
60 2
v  v 02 
0  102
2
2

 ΔE   3.000 J.
b) Calculando o módulo da aceleração:
Δv
0  10
a 

 a  50 m/s2 .
Δt
0,2
[Resposta do ponto de vista da disciplina de Química]
c) Reação química de decomposição da azida de sódio formando sódio metálico e nitrogênio
gasoso: 2NaN3 (s)  2Na(s)  3N2 (g).
d) Cálculo do volume V de gás nitrogênio formado pela decomposição de 65 g de azida de
sódio sob pressão atmosférica de 1atm e temperatura de 27 C :
NaN3  65
2NaN3 (s)  2Na(s)  3N2 (g)
2  65 g
3 mols
65 g
1,5 mol
T  27  273  300 K
R  0,08 atm. .mol1.K 1
P V  nR T
1 V  1,5  0,08  300
VN  36 L
2
Resposta da questão 3:
[Resposta do ponto de vista da disciplina de Química]
a) Teremos:
Para n mols de butano:
1 mol C4H10
58 g
n
mC H
4 10
mC H  58n g
4 10
Para n mols de propano:
1 mol C3H8
44 g
n
mC H
3 8
mC H  44n g
3 8
mC
4H10
 mC
3H8
 1,02 g
58n g  44n g  1,02 g
n  0,01 mol
ntotal  2n  2  0,01  0,02 mol
b) Para a mistura de propano e butano, teremos:
12
24 L
1 mol
V
0,02 mol
V  0,48 L  480 mL
Vazão do gás 
48 mL.min1 
V (volume)
t (tempo)
480 mL
t
t  10 min
c) Teremos:
t  10 min  10  60 s  600 s
S
t
S
1
2,5m.s 
600s
S  1500 m
Velocidade 
ou
S  1,5  103 m
[Resposta do ponto de vista da disciplina de Física]
a) Química.
b) Química.
c) Dado: vm  2,5 m/s.
Do item anterior: t  10 min  600 s.
D  vm Δt  2,5  600  D  1.500 m.
Resposta da questão 4:
Dados: f  0,25 Hz; r  2 m; VR  4 m/s; π  3.
a) Como se trata de movimento circular uniforme, somente há a componente centrípeta da
aceleração.
VT  2 π f r  2  3  0,25  2 
a 
VT
r
2

32

2
VT  3 m/s.
a  4,5 m/s2 .
 
b) A figura mostra a velocidade resultante U da bola num ponto qualquer da trajetória.
13
U2  VT2  VR2  32  42 
c) cos θ 
VR 4
  0,8 
U
5
U  5 m/s.
θ  arccos0,8.
Resposta da questão 5:
a) Dados: m  30 kg; g  10 m/s2; H  2,5 m.
Analisemos a figura a seguir:
Por semelhança de triângulos:
d
h
H 2,5
 2  h 
 h  1,25 m.
H
d
2
2
O sistema é conservativo. Com referencial na base do plano, vem:
A
B
A
A
B
B
EMec
 EMec
 ECin
 EPot
 EB
Cin  EPot  0  m g H  ECin  m g h 
E  EB
Cin  m g H  h   30  10  1,25 
E  375 J.
Calculando a velocidade e a quantidade de movimento (Q) no ponto B:
m vB2
2 E 2  375
 E  vB2 

 25  vB  5 m/s.
2
m
30
Q  m vB  30  5 
Q  150 kg  m/s.
b) Dados: m  30 kg; g  10 m/s2 ; cos30  0,9.
Como não há atritos a considerar, a força de contato entre o escorregador e a criança é a
força normal, de intensidade F.
14
F  Py  Pcos θ  m g cos30  30  10  0,9 
F  270 N.
c) Dados: m  30 kg; g  10 m/s2 ; sen30  0,5.
A força resultante sobre a criança é a componente tangencial do peso, Px.
Fres  Px  m gsen θ  m a  m gsen30  10  0,5 
Resposta da questão 6:
5 kcal V
3L
;

; 1 cal  4 J.
a) Dados : E 
V
Δt min
L
E V 5 kcal 3 L
kcal 15  4  kJ
P



 15

V Δt
L
min
min
60 s

a  5 m/s2.
P  1 kW  1.000 W.
b) Dados: Δt  20 min  1.200 s.
E  P Δt  1.000  1.200 
E  1,2  106 J.
5 kcal
; Δt  1 min  60 s; 1 cal  4 J.
c) Dados : Pb  100 W; E V 
L
A energia basal consumida em 1 min é:
Eb  Pb Δt  100  60  6.000 J  1.500 cal  1,5 kcal.
O volume consumido de O2 pode ser obtido por proporçăo direta:
5 kcal  1 L
1,5
 V

V  0,3 L.

5
1,5 kcal  V
Resposta da questão 7:
Dados: f  15 m; D  1,5  109 m; L 1,5  1011m.
a) O Sol comporta-se como objeto impróprio para o espelho, portanto a imagem forma-se no
foco principal. Assim, p' = 15 m, conforme ilustra a figura.
Sendo D o diâmetro da imagem, por semelhança de triângulos:
D
f
D
15
15



 D

9
11
DSol L
1,5  10
1,5  10
102
D  0,15 m.
b) Dados: DE  10 m; S1  1 kW/m2.
15
A densidade de potência (S) é a razão entre a potência recebida e a área de captação (A).
Pela conservação da energia:
2
P1  A1 S1
π D2
π DE
P
S
 P  A S

 S1 
S 
A
4
4
P2  A 2 S
S
2
DE
S1
D
2

100  1.000
0,152

S  4,44  106 W/m2 .
c) Dados: m  0,6 kg  600 g; Δt  4 s; c  1 J / g  K.
Como todo calor recebido é usado no aquecimento do disco de alumínio, temos:
A1 S1 Δt
Q  P Δt  m c ΔT  A1 S1 Δt  ΔT 

m c
ΔT 
3
102
 1.000  4
4

600  1
ΔT  500 K.
Resposta da questão 8:
a) Dados: ΔE  3,6  104 J/g; m  0,1g/min.
m
Δt
Usando análise dimensional:
g
ΔE ΔE m
J
J
3.600 J
W


 P  3,6  10 4
 0,1
 3.600


Δt
m Δt
g
min
min
60 s
W  60 W.
b) Dado: m = 2,5 g.
Usando os dados e resultados do item anterior e análise dimensional, vem:
3.600 J
2,5 g
E

 E  9  104 J.
g
min
0,1
min
c) Dados:
p0  1 atm; V0  750 ; Cv  30
atm
J
J
; R  0,08
8
;
mol K
mol K
mol K
T0  27 C  300 K; 1 mol  25 .
O excesso de dados com valores aproximados e inconsistentes permite duas resoluções que
chegam a diferentes resultados.
Calculando o número de mols:
- Pela equação de Clapeyron:
p0 V
1 750
p0 V  n R T0  n 

 n  31,25 mol.
RT
0,08  300
- Por proporção direta:
16
25

750
 1 mol
 n
n
750
 n  30 mol.
25
Nota: por comodidade, será usado nos cálculos a seguir o segundo resultado: n = 30 mol.
- A energia liberada pela queima da vela é absorvida pelo ar na forma de calor, aquecendo o
ar do recipiente.
E  Q  n Cv ΔT  ΔT 
Q
9  10 4


n Cv
30  30
ΔT  100 K  100  C.
- A queima da vela ocorre a volume constante, portanto toda a energia liberada é usada para
aumentar a energia interna do gás. Como o ar deve ser tratado como gás perfeito, usando
a expressão da variação da energia interna para um gás diatômico, vem:
E  ΔU 
2 ΔU
5
9  10 4
n R ΔT  ΔT 


2
5 n R 5  30  8
ΔT  75 K  75  C.
Nota: por comodidade, será usado nos cálculos a seguir o primeiro resultado: ΔT  100K.
d) Aplicando a equação geral dos gases ideais:
p0 V
pV
1
p
4



 p  atm 
T0
T0  ΔT
300 300  100
3
p  1,33 atm.
Resposta da questão 9:
a) Dados: V  300 V; d  5 mm  5  103 m.
A figura ilustra os dados.
Como se trata de campo elétrico uniforme, EA = EB = EC = E.
Ed  V  E 
V
300

 60  103 
d 5  103
E  6  10 4 V/m.
b) Da figura: xA = 1 mm e xB = 4 mm.
VAB  E dAB  E  xB  x A   6  104  4  1  103

VAB  180 V.
Como os pontos B e C estão na mesma superfície equipotencial:
VBC  0 V.
17
c) Dado: q  1,6  1019 C.
Analisando a figura dada: VCA  VBA  VAB  180V.
τ  q VCA  1,6  1019   180  
τ  2,88  1017 J.
Resposta da questão 10:
a) A constante α é dada pela declividade da reta.
α  tgθ 
18  12
6


120  20 100
α  0,06
Ω
.
C
b) Dados: T0  20 C  R0  12 Ω  do gráfico  ; i  10 A.
A 20 °C:
V  R i  12  10 
V  120 V.
c) À temperatura TM:
V  R i  120  R  5   R  24 Ω.
Do gráfico: R  24Ω 
TM  220 °C.
Resposta da questão 11:
a) Da expressão da distância percorrida no movimento uniforme:
d  v Δt  2 L  c Δt 
Δt 
2L
.
c
b) Considerações:
- como a largura de um dente é igual à largura de um espaço vazio, o comprimento da
circunferência envolvente da roda corresponde à largura de 2 N dentes;
18
- assim, a distância entre um ponto central entre dentes e o dente seguinte é igual à largura
de um dente.
- a frequência da roda dentada é V voltas por segundo. Então o período (T) é:
1
T .
V
Estabelecendo proporção direta:
2 N dentes  T

 1 dente  Δt
Δt 
 2 N Δt  T  Δt 
1
T
 V
2N 2N

1
.
2NV
c) Dados: L = 8600 m; N = 750; V = 12 voltas por segundo.
Os intervalos de tempo calculados nos itens anteriores são iguais.
Então:
2 L
1

 c  4 L N V  4  8.600  750  12  309.600.000 
c
2 N V
c  3,1 108 m/s.
Resposta da questão 12:
a) No gráfico, nota-se que o movimento de Batista é uniformemente variado. Entendendo
como aceleração o módulo da componente tangencial da aceleração ou a aceleração
escalar, tem-se:
Δv B
40
4
1
aB 



 aB  0,2 m/s2 .
Δt B
20  0 20 5
b) No gráfico velocidade x tempo, a distância percorrida é numericamente igual à “área” entre
a linha do gráfico e o eixo dos tempos.
Assim:
50  5

 dA  125 m.
dA  2

d  50  30  4  d  160 m.
B
 B
2
c) A velocidade escalar média de Arnaldo no intervalo pedido é:
d
125
vA  A 
 v A  2,5 m/s.
Δt A
50
Resposta da questão 13:
a) Dados: P = 4 W; Δt  5 s.
E  P Δt  4  5  E  20 J.
b) Dados: m = 0,2 kg; R  5 cm  5  102 m.
A energia cinética das duas esferas é:
19
E2
ω
m v2
2
 m  ω R   E  m ω2 R2 
2
1 E
1

R m 5  10 2
20 100

100
0,2
5

ω  200 rad/s.
c) A aceleração (a) da esfera tem duas componentes: tangencial (aT ) e centrípeta (aC ).
- Componente tangencial:
v  aT t  ω R  a T t  a T 
ω R 200  5  102

t
5
 aT  0,2 m/s2 .
- Componente centrípeta:

aC  ω2 R  2  102

2
 5  10 2  4  10 4  5  10 2  aC  2  103 m/s 2.
Comparando os valores obtidos, a componente tangencial tem intensidade desprezível.
Então a intensidade da resultante é igual à da componente centrípeta.
aT  aC  a  aC  2  103 m / s2.
Aplicando o Princípio Fundamental da Dinâmica:
Fres  m a  0,2  2  103  0,4  103

Fres  400 N.
d) α 
aT
2

 0,4  102  α  40 rad/s2 .
2
R
5  10
Resposta da questão 14:
Nota: o termo órbita em torno do Sol é redundante, pois a órbita já é em torno de algo.
a) a força que o satélite exerce sobre a Terra é desprezível. Então, a resultante centrípeta
sobre a Terra é a força gravitacional que o Sol exerce sobre ela, conforme indica a figura.
Rcent  FST  MT ω2T R 
ωT 
G MS
R3
G MS MT
R
2
 ωT2 
G MS
R3

.
b) O período de translação do satélite é igual ao período de translação da Terra:
20
TA  TT  1ano  3,14  107 s.
ωA 
2π
2  3,14

TA
3,14  107

ωA  2  107 rad/s.
c) A força resultante gravitacional sobre o satélite é a soma vetorial das forças gravitacionais
que o satélite recebe do Sol e da Terra, conforme ilustra a figura.
Fres  FS  FT 
G MS m
R  d 
2

G MT m
d2

 M
M 
S
Fres  G m 
 T .
 R  d 2 d2 


Resposta da questão 15:
a) A área total é igual à soma das áreas das seis faces.
A  2  2  3  2  4  3  4 
A  52 m2.
b) Dados: k  5  102 J(s  m  C); ε  26cm  26  102 m; Ti  20C; Te  40C.
Para manter a temperatura constante, a potência do aquecedor deve compensar o fluxo de
calor para o meio.
Assim:
PΦ
2
k A ΔT 5  10  52  20   -40  

 6  102 W 
2
ε
26  10
P  0,6 kW.
c) Da expressão da energia consumida:
E  P Δt  0,6  24  E  14,4 kWh.
Resposta da questão 16:
a) Dados: D = 60 km = 6.000 m; C = 80 cal/m; ET = 2.000 kcal.
Calculando a energia consumida (E1) em uma caminhada:
 80 cal
1 m
 E1  6.000  80  480.000 cal  E1  480 kcal.

6.000 m  E1
Para a percentagem P temos:
100%  2.000 kcal
100  480
 P

480 kcal
2.000
 P% 
 P  24%.
21
b) Dados: M = 80 kg; g = 10 m/s2; h = 300 m.
Da expressão da energia potencial:
C  m g h  80  10  300  C  2,4  10 4 J 
24  10 4 J
4 J/cal

C  6  10 4 cal.
c) Dados: m = 2,4 kg = 2400 g.
Do Note e adote, para perder 2400 g de gordura terá que queimar a quantidade de energia:
E  2400  9  21600 kcal.
Estabelecendo proporção direta:
 480 kcal
21600
1 caminhada
 N


480
N caminhadas  21600 kcal
N  45.
Resposta da questão 17:
O gráfico destaca os valores relevantes para a resolução da questão.
a) Como o resistor e a lâmpada estão em série, a corrente é a mesma nos dois.
Do gráfico:
V  2,5 V  iR  i  0,04 A.
b) A força eletromotriz da bateria é E = 4,5 V. A tensão no resistor é VR.
VE  E  VR  4,5  2,5  VR  2,0 V.
Aplicando a 1ª lei de Ohm:
VR  R i R  2  R  0,04 
 R
2
0,04

R  50 Ω.
c) Com a nova bateria (E’ = 3 V), para a potência total PT = 60 mW, a corrente na lâmpada é
i' .
P  E' i'
 60  3 i'
 i'  i'R  20 mA  0,02 A  2  102 A.
A potência PR dissipada no resistor é:


2
2
PR  R i'R
 50 2  102  50  4  10 4  20  10 3 W 
PR  20 mW.
22
Resposta da questão 18:
a) Dado: f = 33 rpm.
33 rot 33 rot
f

 f  0,55 Hz.
min
60 s
ωf  2 π f  ωf  2  3  0,55  ωf  3,3 rad / s.
b) Dados: α = 1,1 rad/s2; ω0 = 0.
Da equação da velocidade angular para o movimento circular uniformemente variado:
ω
3,3
ωf  ω0  α t f  t f  f 
 t f  3 s.
α
1,1
c) Dados: μ e = 0,09; g = 10 m/s2; r = 10 cm = 0,1 m.
A componente de atrito da força que o disco aplica na caixa de fósforos exerce a função de
resultante centrípeta. A caixa começa a se deslocar em relação ao disco no instante em que
a força de atrito atinge intensidade máxima.
Da figura:
Fmáx  Fcent
2
2
at
r es
 μ e N  m ωc r  μ e m g  m ωc r 

N

P

m
g

ωc 
μe g
r
 ωc 
0,09  10
 9 
0,1
ωc  3 rad / s.
d) Aplicando os resultados obtidos nos itens anteriores na equação de Torricelli para o
movimento circular uniformemente variado:
ωc2  ω02  2 α Δθ  Δθ 
ωc2
32


2 α 2  1,1
Δθ  4,1 rad.
Resposta da questão 19:
a) Dados: PT = 100 GW = 100  109 W; I = 250 W/m2.
I
PT
A
 A
PT 100  109

I
250

A  4  108 m2 .
b) Dados: P = 0,8 PT; 1 ano = 3  107 s.
EB  P t  EB  0,8 PT t  0,8  100  109  3  107

EB  2,4  1018 J.
c) Dado: equivalente energético do petróleo igual a 4  107 J/L.
23
 4  107 J



18
2,4  10 J 
1L
 V
V
2,4  1018
4  107

V  6  1010 L.
d) Dado: c = 3  108 m/s.
EB  m c 2  m 
EB
c2

2,4  1018

3  108

2

2,4  1018
9  1016

m  26,7 kg.
Resposta da questão 20:
Dados: M = 6  1024 kg; m = 1016 kg; v0 = 30 km/s = 3  104 m/s; 1 megaton = 4  1015 J.
a) Pi  m v0  1016  3  104  Pi  3  1020 kg  m / s.


2
16
4
m v 02 10  3  10

 Ec  4,5  1024 J.
b) Ec 
2
2
c) Trata-se de um choque inelástico. A massa do meteoro é desprezível em relação à massa
da Terra, por isso, depois do choque, a massa do sistema é apenas a massa da Terra, pois:
6  1024  1016  6,00000001 1024  6  1024.
Pela Conservação da Quantidade de movimento:
m v 0 3  1020
Antes
QSist
 QDepois

m
v

M

m
v

v


 5  10 5 m / s 


o
Sist
M
6  1024
v  0.
O choque do meteoro com a Terra praticamente não altera a velocidade da Terra.
d) Pela resposta do item anterior, conclui-se que toda energia cinética do meteoro é dissipada
na colisão. Passando para megaton:
 4  1015 J  1 megaton
4,5  1024

 Edissip 


24
4  1015
 Edissip
 4,5  10
Edissip  1,125  109 megaton.
Resposta da questão 21:
a) Aplicando a 1ª Lei de Ohm na 2ª e 4ª linhas:
1,1

I2 
 0,25 A.

4,4
V 
V R I  I

0,96
R 
I 
 0,60 A.
 4
1,6
V(V)
1,14
1,10
1,05
0,96
0,85
R(  )
7,55
4,40
2,62
1,60
0,94
I(A)
0,15
0,25
0,40
0,60
0,90
b) Substituindo os valores da tabela do item anterior:
24
Obs.: no eixo das tensões, os valores começam a partir de V = 0,7 V, por isso a reta não
cruza o eixo das correntes no valor da corrente de curto circuito.
c) Substituindo os dois primeiros valores de V e de I da tabela na equação do gerador e
subtraindo membro a membro as duas equações:
1,14  ε  r  0,15 

0,04
V  ε  r I  1,10 ε  r  0,25  
 r
 r  0,4 Ω.
0,1


0  0,10 r
 0,04
1,14  ε   0,4  0,15 
 ε  1,14  0,06  ε  1,2 V.
Obs.: A equação dessa bateria é:
V  1,2  0,4 I.
Para V = 0,7 V:
1,2  0,7
0,7  1,2  0,4 I  I 
 i  1,25 A.
0,4
Esse é o valor em que a linha do gráfico corta o eixo das correntes, como assinalado no gráfico
do item anterior.
25