∑ ∑ ∑ ∑ ∑ ∑

ARIVIDADE EXTRACLASSE
Treliça
•
Treliça: estrutura composta de barras (metálicas ou de madeira) unidas por rótulas (nós) nas
suas extremidades.
Problema da treliça
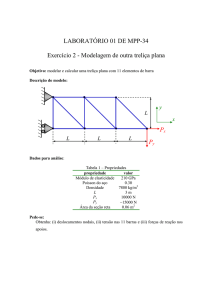
Determinar as forças que atuam nas junções da treliça abaixo:
•
Forças que atuam na treliça: 17
•
O número de junções (j) está relacionado com o número de componentes da treliça (m):
2j-3 = m
Neste caso: 2 (10) – 3 = 17
•
Logo, as componentes das forças são determinadas pelas condições de equilíbrio nas junções.
Sejam Fx e Fy as componentes horizontal e vertical das forças, respectivamente.
Considerando α = sen(45º) = cos(45°) e supondo pequenos deslocamentos, as condições de equilíbrio
são:
•
Junção 2:

 Fx   f1  f 4   f5  0


 Fy    f1  f3   f5  0
•
Junção 3:

 Fx   f 2  f 6  0


 Fy  f3  F1  0
•
Junção 4:

 Fx   f 4  f8  0


 Fy   f 7  0
•
Junção 5:
•
Junção 6:
•
Junção 7:
•
Junção 8:
•
Junção 9:
•
Junção 10:

 Fx   f5  f 6   f9  f10  0


 Fy   f5  f 7   f9  F2  0

 Fx   f8   f9  f12   f13  0


 Fy   f9  f11   f13  0

 Fx   f10  f14  0


 Fy  f11  0

 Fx   f12   f16  0


 Fy   f15   f16  0

 Fx   f13  f14  f17  0


 Fy  f13  f15  F3  0
 F
x
  f16  f17  Fh  0
A formulação matricial do sistema A.x = b, é dada por:
Exercício: Resolver o sistema usando o SCILAB e o soft Calculo Numérico 5.1