Noções de Eletrônica digital

Eletrônica digital I - Introdução, funções lógicas elementares
1-) Uma introdução aos números
(início da página)
Número, coisa banal que usamos sempre. Mas se alguém pergunta: o que é número? Bem,
pode ser dito que é um símbolo que representa uma coleção de objetos iguais.
Seja, por exemplo, o objeto representado por *, que chamamos de estrela. Assim a coleção
*** seria representada por 3*, a coleção ***** por 5*, etc. Simples não? Mas imagine a
tecnologia sem números. Seria impossível. A seguir, alguns conceitos mais avançados.
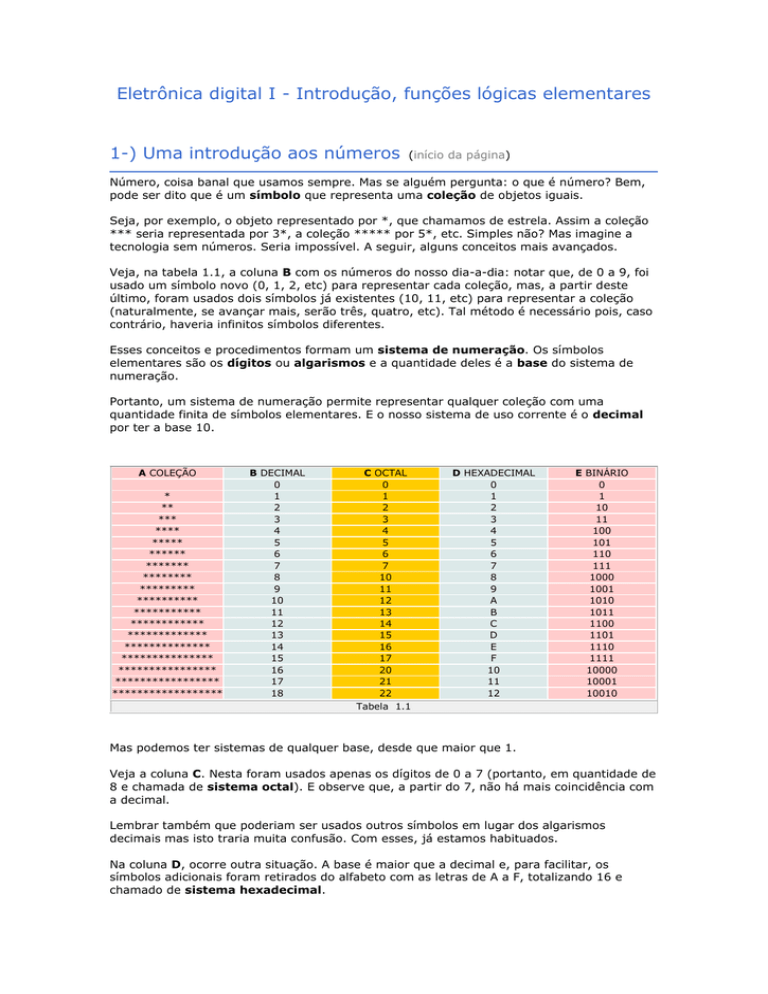
Veja, na tabela 1.1, a coluna B com os números do nosso dia-a-dia: notar que, de 0 a 9, foi
usado um símbolo novo (0, 1, 2, etc) para representar cada coleção, mas, a partir deste
último, foram usados dois símbolos já existentes (10, 11, etc) para representar a coleção
(naturalmente, se avançar mais, serão três, quatro, etc). Tal método é necessário pois, caso
contrário, haveria infinitos símbolos diferentes.
Esses conceitos e procedimentos formam um sistema de numeração. Os símbolos
elementares são os dígitos ou algarismos e a quantidade deles é a base do sistema de
numeração.
Portanto, um sistema de numeração permite representar qualquer coleção com uma
quantidade finita de símbolos elementares. E o nosso sistema de uso corrente é o decimal
por ter a base 10.
A COLEÇÃO
*
**
***
****
*****
******
*******
********
*********
**********
***********
************
*************
**************
***************
****************
*****************
******************
B DECIMAL
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
C OCTAL
0
1
2
3
4
5
6
7
10
11
12
13
14
15
16
17
20
21
22
Tabela 1.1
D HEXADECIMAL
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
10
11
12
E BINÁRIO
0
1
10
11
100
101
110
111
1000
1001
1010
1011
1100
1101
1110
1111
10000
10001
10010
Mas podemos ter sistemas de qualquer base, desde que maior que 1.
Veja a coluna C. Nesta foram usados apenas os dígitos de 0 a 7 (portanto, em quantidade de
8 e chamada de sistema octal). E observe que, a partir do 7, não há mais coincidência com
a decimal.
Lembrar também que poderiam ser usados outros símbolos em lugar dos algarismos
decimais mas isto traria muita confusão. Com esses, já estamos habituados.
Na coluna D, ocorre outra situação. A base é maior que a decimal e, para facilitar, os
símbolos adicionais foram retirados do alfabeto com as letras de A a F, totalizando 16 e
chamado de sistema hexadecimal.
Na coluna E foi usada a menor base possível. Apenas 2 símbolos, 0 e 1, formando, portanto,
o sistema binário. Notar que, quanto menor a base, maior a quantidade de dígitos
necessária para representar a mesma coleção.
2-) Convenções e conversões
(início da página)
Conforme já visto, para evitar uma proliferação de símbolos de difícil memorização, sistemas
de outras bases usam os mesmos dígitos do decimal e é necessária alguma indicação para
evitar confusão (por exemplo 11 decimal é diferente de 11 octal).
A convenção clássica é númerobase: 1110, 1216, etc. Mas, por questão de simplicidade, aqui é
adotada a convenção da linguagem C de programação:
Decimal
sem indicação (12, 350, etc)
Octal
prefixo 0 (035, 012, etc)
Hexadecimal
prefixo 0x (0x11, 0xCC, etc)
Binário
sem indicação (11, 1101, etc)
Portanto, não será usado zero à esquerda, que numericamente não tem sentido, a não ser
para indicar base octal. Mas não poderá haver confusão entre o decimal e o binário? (por
exemplo: 11 decimal é diferente de 11 binário). É evidente que sim. Entretanto, na prática,
valores não são expressos em binário. Simplesmente porque são muito extensos (se 16 em
binário é 10000 imagine, por exemplo, 250000). Em geral, a representação de um número
binário é explicitamente informada ou fica subentendida pela própria aplicação.
A conversão de decimal para binário, octal, hexadecimal ou vice-versa dá um pouco de
trabalho mas é fácil. De binário para octal, hexadecimal ou vice-versa, ela é ainda mais fácil
porque guarda relações com potências de 2 (8 = 23 e 16 = 24):
Decimal para binário
Divide-se o número sucessivamente por 2 até que o quociente seja 1, que será o dígito
binário mais significativo e os demais serão os restos da divisão, em ordem inversa.
Exemplo: seja o número decimal 13.
13/2 = (resto 1) 6. 6/2 = (resto 0) 3. 3/2 = (resto 1) 1.
Então, 13 em binário é 1101.
Binário para decimal
Multiplicam-se os dígitos binários por 2 elevado à potência correspondente à respectiva
posição, considerando 0 para o dígito menos significativo. Exemplo: seja o número binário
1101.
1 x 23 + 1 x 22 + 0 x 21 + 1 x 20 = 8 + 4 + 0 + 1 = 13.
Octal para binário
Juntam-se os binários equivalentes a cada dígito. Exemplo 013 ( 1 octal é 10 binário e 3
octal é 11 binário). Assim 013 = 1011.
Binário para octal
Separam-se os grupos de 3 dígitos da direita para a esquerda e juntam-se os equivalentes
octais. Exemplo: 1011  1 011 e, como zero à esquerda é desprezado, 1 11 ou em octal 1 3
ou 013 conforme convenção.
Hexadecimal e binário
De forma semelhante ao octal mas, na conversão do binário, são separados grupos de 4.
Exemplos: 0x1A = 11010 e de 11010 para hexadecimal: 1 = 1 hexa (ou 0x1) e 1010 = A
hexa (ou 0xA) e portanto 0x1A.
3-) Uma introdução à eletrônica digital
(início da página)
O processamento de informações em escala ampla por circuitos eletrônicos só é possível na
prática se elas estiverem na forma de números binários.
Seja um exemplo: alguém deseja um circuito que processe grandezas de 1 a 1 000 000.
Então pode-se considerar 1 volt para cada unidade. Assim tal circuito deveria trabalhar com
tensões de 0 a 1 milhão de volts. Não é possível (nem seguro) na prática. Mas pode-se
imaginar um circuito que trabalhe na faixa de 0 a 100 volts e considerar 100/1 000 000 cada
unidade. Mas 100/1 000 000 = 0,0001 volt. Seria muito difícil e instável algo para
reconhecer variações tão pequenas de tensão.
Isto é apenas um exemplo grosseiro. Existem muitas outras funções que não podem ser
executadas por circuitos de variações contínuas, chamados analógicos. Mas não significa o
desaparecimento deles. Pelo contrário. Certas funções só podem ou são melhor executadas
pelos mesmos.
A facilidade do processamento de números binários decorre da existência de apenas dois
dígitos, 0 e 1, que podem ser representados por 2 níveis de grandezas como tensão ou
corrente (exemplo 0 = 0 volt e 1 = 5 volts). Na realidade, tais níveis não são valores únicos,
mas sim faixas. Veja exemplo com um componente eletromecânico:
Um relé de bobina com tensão nominal de 6 V certamente irá acionar com tensões na faixa
de 5 a 7 V e não acionará com tensões de 0 a 2 V. Então o nível lógico 0 será a faixa de 0-2
V e o nível 1, a faixa de 5-7 V. A faixa intermediária, 2 a 5 V, será provavelmente instável (a
bobina poderá acionar ou não) e o projeto do circuito não deve permitir tensões nessa faixa,
o que não é difícil. Com componentes eletrônicos ocorre algo semelhante. Operando desta
forma, o circuito se torna altamente imune a interferências, diferenças de características de
componentes, variações de temperatura e outros.
A contrapartida da facilidade é a necessidade de muitos circuitos pois, como já visto, base
pequena implica muitos dígitos. Mas isso foi contornado pela integração em larga escala dos
mesmos.
Observação: no estudo e análise de circuitos, são comuns as denominações nível baixo e
nível alto para 0 e 1 respectivamente. Em vários casos, são mantidas as abreviações
inglesas L e H (low, high).
3-) Informações binárias e processamento
(início da página)
Na Eletrônica Digital, o conceito de número binário conforme primeiro tópico é ampliado
para informação binária. Ou seja, o conjunto de 0s e 1s não é necessariamente um
número. Pode representar uma instrução, um caractere ou qualquer outra informação. Isto
só dependerá do projeto do circuito e das instruções que lhe forem dadas.
Uma analogia: se você mora no sexto andar de um prédio e seu apartamento tem o
"número" 601, isto não significa necessariamente que abaixo do seu andar existem 600
apartamentos do prédio. O mais provável é que 6 identifique o andar e 01, um apartamento
neste.
Quanto ao processamento, é natural que todos esperem da eletrônica digital operações como
soma, multiplicação, comparação, memorização e tantas outras. Mas todas têm seu ponto de
partida nas funções lógicas elementares, objeto de estudo nos próximos tópicos.
4-) Blocos lógicos e funções lógicas
(início da página)
A figura 4.1 representa um bloco lógico (ou porta lógica, nos casos mais simples)
genérico, ou seja, um circuito simbolizado pelo quadrado com uma ou mais entradas
lógicas A, B, etc e uma ou mais saídas lógicas S1, S2, etc.
Fig 4.1
As entradas e saídas lógicas só assumem valores correspondentes aos níveis lógicos 0 e 1.
Em termos absolutos, considerando o escopo desta matéria, não interessa saber quais os
valores de tensões e correntes, pois isso depende do projeto do circuito. Assim, dizemos que
entradas e saídas só podem ser 0 ou 1.
Um bloco lógico executa uma determinada função lógica para a qual foi projetado. Essa
função determina os valores que as saídas assumem para cada combinação de valores das
entradas. Tais relações são muitas vezes exibidas em forma de tabelas de verdade.
A
B
S
0
0
0
0
1
0
1
0
0
1
1
1
Tabela 4.1
Na Tabela 4.1, exemplo de uma tabela de verdade hipotética para um circuito com duas
entradas, A e B, e uma saída S.
Notar que o número de linhas (sem contar o cabeçalho) da tabela de verdade depende do
número de entradas pois todas as combinações devem ser consideradas. No exemplo dado,
com duas entradas, 22 = 4. Assim, no caso de 3, haveria 23 = 8 linhas.
Os blocos lógicos são em geral implementados na forma de circuitos integrados.
Naturalmente, além das entradas e saídas lógicas, há ligações para tensão de alimentação e
massa (GND). Alguns circuitos exigem também uma tensão simétrica -V conforme figura.
Isso depende da tecnologia usada e do tipo.
Nesta série de páginas, tratamos especificamente da lógica dos circuitos. Assim, as ligações
de alimentação e massa são representadas apenas quando necessário.
Por via de regra, os blocos serão tratados como caixas pretas, ou seja, seus circuitos
internos não serão objetos de estudo. Apenas as funções que executam.
Além das tabelas de verdade, as funções lógicas podem ser representadas por funções
algébricas, que pertencem à chamada Álgebra de Boole, assunto de tópico mais adiante.
5-) A função E (AND)
(início da página)
Fig 5.1
É definida como a função lógica de duas ou mais entradas e uma saída, tal que o valor da
saída é 1 se todas as entradas são 1 e 0 nos demais casos.
A Figura 5.1 dá um exemplo de um circuito com elementos eletromecânicos (relés) que
executam a função.
Considerando os níveis de tensão 0 V e + V para os níveis lógicos 0 e 1 respectivamente,
podemos concluir que a saída S só terá valor 1 se ambos os relés (R1 e R2) estiverem
acionados, isto é, A = 1 e B = 1. Nos demais casos temos S = 0.
A
B
S
0
0
0
0
1
0
1
0
0
1
1
1
Tabela 5.1
A Tabela 5.1 acima é a tabela de verdade para a função E com duas variáveis de entrada.
A Figura 5.2 dá o símbolo usual para a função, com duas variáveis de entrada.
Fig 5.2
A expressão algébrica conforme álgebra de Boole (ou expressão booleana) é dada por:
S=A.B
É comum a omissão do ponto. Assim, também pode ser escrita S = AB
6-) A função OU (OR)
(início da página)
Fig 6.1
É definida como a função lógica de duas ou mais entradas e uma saída, tal que o valor da
saída é 1 se pelo menos uma entrada é 1 e 0 se todas as entradas são 0.
A Figura 6.1 dá um exemplo de um circuito com elementos eletromecânicos (relés) que
executam a função.
Considerando o nível lógico 0 como 0 V e 1 como +V, podemos concluir que a saída S é zero
se ambas as entradas são zero e um se pelo menos uma das entradas é um.
A
B
S
0
0
0
0
1
1
1
0
1
1
1
1
Tabela 6.1
Tabela 6.1
A Tabela 6.1 ao lado é a tabela de verdade para a função OU com duas variáveis de entrada.
A Figura 6.2 dá o símbolo usual para a função, com duas variáveis de entrada.
Fig 6.2
A expressão conforme álgebra de Boole (ou expressão booleana) é dada por:
S = A + B (não confundir com soma algébrica comum. Não é equivalente).
7-) A função NÃO (NOT)
(início da página)
Fig 7.1
É definida como a função lógica de uma entrada e uma saída tal que a saída é 1 se a entrada
é 0 e 0 se a entrada é 1.
A Figura 7.1 dá um exemplo de um circuito com elemento eletromecânico (relé) que executa
a função.
A
S
0
1
1
0
Tabela 7.1
A Tabela 7.1 acima é a tabela de verdade para a função NÃO.
A Figura 7.2 dá o símbolo usual para a função (a função é também chamada de inversora e,
quando situada numa entrada ou saída de um outro bloco lógico, pode ser representada por
um pequeno círculo).
Fig 7.2
A expressão conforme álgebra de Boole (ou expressão booleana) é dada por:
S = A.
8-) A função OU EXCLUSIVO
A
B
S
0
0
0
0
1
1
1
0
1
(início da página)
1
1
0
Tabela 8.1
Tabela 8.1
É definida como a função lógica tal que, no caso de duas entradas, o valor da saída é 1 se as
entradas são diferentes e 0 se as entradas são iguais.
A Tabela 8.1 ao lado é a tabela de verdade para a função OU EXCLUSIVO com duas variáveis
de entrada.
A Figura 8.1 dá o símbolo usual para a função, com duas variáveis de entrada.
Fig 8.1
A expressão conforme álgebra de Boole (ou expressão booleana) é dada por:
S = A  B.
9-) Funções derivadas
(início da página)
Aqui são dadas duas funções derivadas de uso bastante comum, formadas pela combinação
das funções E e OU com a função NÃO. As tabelas de verdade são facilmente dedutíveis.
Fig 9.1
Figura 9.1 (a) - função NÃO E (NAND):
S = (A . B).
Figura 9.1 (b) - função NÃO OU (NOR):
S = (A + B).
10) Alguns princípios da álgebra de Boole
(início da página)
Também chamada de álgebra Booleana, é um conjunto de símbolos, propriedades,
teoremas, etc que permitem operações com expressões lógicas, de forma semelhante às
operações aritméticas.
Variáveis booleanas ou lógicas são as que só podem assumir valores binários, ou seja, 0
ou 1. As variáveis A, B, S dos tópicos anteriores são exemplos.
Expressões booleanas são as que indicam igualdades e operações com variáveis lógicas.
São exemplos as expressões nos tópicos anteriores.
A página Eletrônica digital I-2 dá, em forma de tabela, um conjunto de igualdades,
postulados e propriedades usados no estudo e na simplificação de circuitos lógicos.
11) Blocos com mais de duas entradas
(início da página)
O bloco NÃO, por sua natureza, só admite uma entrada e uma saída. Os blocos E e OU (e
seus derivados) podem ter qualquer número (2) de entradas. Ou seja, o limite é apenas
prático. Nas figuras abaixo, exemplo de bloco E de 4 entradas (com uma inversora em B) e
NÃO OU, também de 4 entradas.
Fig 11.1
Para o bloco (a) da Figura 11.1:
S = ABCD
Para o bloco (b) da Figura 11.1:
S = A+B+C