1) Quando o cabo de um elevador se quebra, os

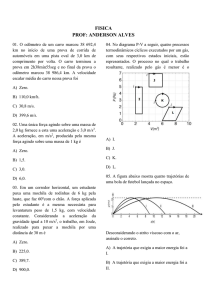
1) Quando o cabo de um elevador se quebra, os freios de emergência são acionados contra trilhos
laterais, de modo que esses passam a exercer, sobre o elevador, quatro forças verticais constantes e
iguais a f , como indicado na figura. Considere g = 10m/s£.
Suponha que, numa situação como essa, a massa total do elevador seja M = 600kg e que o módulo
de cada força f seja | f | = 1350N.
Calcule o módulo da aceleração com que o elevador desce sob a frenagem dessas forças.
2) A figura ilustra um bloco A, de massa mÛ = 2,0 kg, atado a um bloco B, de massa m½ = 1,0 kg, por
um fio inextensível de massa desprezível. O coeficiente de atrito cinético entre cada bloco e a mesa é
˜Ý. Uma força F = 18,0 N é aplicada ao bloco B, fazendo com que ambos se desloquem com
velocidade constante.
Considerando g = 10,0 m/s£, calcule
a) o coeficiente de atrito ˜Ý.
b) a tração T no fio.
3) Deseja-se manter um bloco em repouso sobre um plano inclinado 30° com a horizontal. Para isso,
como os atritos entre o bloco e o plano inclinado são desprezíveis, é necessário aplicar sobre o bloco
uma força. Numa primeira experiência, mantém-se o bloco em repouso aplicando uma força
horizontal ù, cujo sentido está indicado na figura 1.
Numa segunda experiência, mantém-se o bloco em repouso aplicando uma força ù' paralela ao plano
inclinado, cujo sentido está indicado na figura 2.
Calcule a razão | ù' | / | ù |
4) O gráfico velocidade contra tempo, mostrado adiante, representa o movimento retilíneo de um
carro de massa m=600kg numa estrada molhada. No instante t=6s o motorista vê um engarrafamento
à sua frente e pisa no freio. O carro, então, com as rodas travadas, desliza na pista até parar
completamente. Despreze a resistência do ar.
a) Qual é o coeficiente de atrito entre os pneus do carro e a pista?
b) Qual o trabalho, em módulo, realizado pela força de atrito entre os instantes t=6s e t=8s?
5) Um carro de corrida, incluindo o piloto, tem 800 kg de massa e seu motor é capaz de desenvolver,
no máximo, 160 kW de potência. O carro acelera na largada, primeiramente, utilizando a tração de
4000 N, que no caso é a máxima permitida pela pista e pelos pneus, até atingir a potência máxima do
motor. A partir daí, o piloto passa a acelerar o carro utilizando a potência máxima do motor até atingir
60 m/s. Suponha que não haja perda de energia por atrito e que todo o trabalho realizado pelo motor
resulte no aumento de energia cinética de translação do carro.
a) Calcule a velocidade do carro ao final da primeira etapa de aceleração.
b) Calcule o tempo gasto na segunda etapa da aceleração.
6) Uma massa é liberada a partir do repouso de uma altura h acima do nível do solo e desliza sem
atrito em uma pista que termina em um "loop" de raio r, conforme indicado na figura. Determine o
ângulo š relativo à vertical e ao ponto em que a massa perde o contato com a pista. Expresse sua
resposta como função da altura h, do raio r e da aceleração da gravidade g.
7) Dois jovens, cada um com 50 kg de massa, sobem quatro andares de um edifício. A primeira
jovem, Heloísa, sobe de elevador, enquanto o segundo, Abelardo, vai pela escada, que tem dois
lances por andar, cada um com 2,0 m de altura.
a) Denotando por W(A) o trabalho realizado pelo peso de Abelardo e por W(H) o trabalho realizado
pelo peso de Heloísa, determine a razão W(A) / W(H).
b) Supondo que são nulas suas velocidades inicial e final, calcule a variação de energia mecânica de
cada jovem ao realizar o deslocamento indicado.
8) A invenção da roda d'água possibilitou a substituição do esforço humano e animal na realização de
diversas atividades. O registro de sua utilização é anterior a 85 a.C. e, nos dias de hoje, ainda pode
ser vista como um mecanismo que auxilia o movimento de outros.
Na figura a seguir, estão ilustrados os principais elementos de um sistema rudimentar de geração de
energia elétrica: a água que jorra do tubo faz a roda girar, acionando um gerador elétrico.
Dados:
Aceleração da gravidade = 10 m/s£
Massa específica da água = 1,0 × 10¤ kg/m¤
Considere um sistema, como o representado acima, com as seguintes características: a vazão é
constante; a água sai do tubo com velocidade desprezível, atingindo a roda 4,0 m abaixo; o
rendimento é de 75%.
Supondo que a potência elétrica oferecida pelo gerador em seus terminais seja 15 kW e desprezando
as perdas de líquido, determine o volume de água que jorra do tubo a cada segundo.
9) Um pêndulo constituído de um fio ideal, de comprimento L = 0,90 m e massa 0,1 kg, é solto a partir
do repouso, da posição inicial mostrada na figura a seguir, formando um ângulo de 60° com a vertical.
Ao longo do tempo, o pêndulo vai tendo o seu movimento amortecido por atrito com o ar, terminando
por parar completamente na posição de equilíbrio.
g = 10m/s£ e cos 60° = 1/2.
Determine a perda da energia mecânica entre o momento inicial e o final.
10) Por volta de 6000 a.C., o homem começou a aplicar a flutuação da madeira na água para
construir balsas e jangadas. Estes meios de transporte ainda são usados no século XXI, em várias
regiões de nosso país.
Considere uma balsa constituída por cinco toras cilíndricas de madeira de massa específica 8,0×10£
kg/m¤, tendo cada tora 0,30 m de diâmetro e 1,8 m de comprimento. A balsa encontra-se em águas
calmas, onde flutua, na horizontal, com parte de seu volume submerso. Um pescador, de 80kg, usa
essa balsa para transportar o produto de seu trabalho.
Desprezando o peso do material utilizado na união das toras, determine:
a) a fração do volume da balsa que fica submersa, antes de o pescador subir nessa embarcação para
iniciar o trabalho;
b) o peso que a balsa pode suportar, além do pescador, flutuando na horizontal, com sua face
superior coincidindo com a superfície livre da água.
Dados:
Aceleração da gravidade = 10 m/s£
Massa específica da água = 1,0 × 10¤ kg/m¤
11) Um cilindro metálico com 4,0 kg de massa é suspenso por uma mola, ocorrendo o equilíbrio
quando esta se alonga 8,0 cm, como ilustra a figura I.
O cilindro agora é mergulhado em um recipiente com água, ocorrendo uma nova situação de
equilíbrio, como ilustra a figura II.
Dados:
massa específica da água ›(H‚O) = 1,0 kg / litro
aceleração da gravidade g = 10 m/s£
massa específica do material do cilindro ›(cilindro) = 8,0 kg/ litro
a) Represente, na figura III, todas as forças que agem sobre o cilindro e escreva o nome do agente
causador de cada uma delas.
b) Calcule a distensão da mola nessa nova situação de equilíbrio, mostrada na figura II.
c) Em um certo instante, o cilindro se desprende da mola e cai, a partir da situação de equilíbrio da
figura II. Despreze a viscosidade da água e determine o tempo que a base do cilindro leva para
percorrer os 70 cm que a separam do fundo do recipiente.
12) Um copo cilíndrico, vazio, flutua em água, com metade de sua altura submersa, como mostra a
fig. 1. Um pequeno objeto, de1,0N de peso, é posto dentro do copo, com cuidado para que não entre
água no copo.
Restabelecido o equilíbrio hidrostático, verifica-se que o copo continua a flutuar, mas com 3/4 de sua
altura submersos, como mostra a fig. 2.
Calcule o peso do copo.
13) Dois empregados utilizam uma barra homogênea, de massa desprezível, apoiada em seus
ombros, para carregar três baldes de 20 kg cada, conforme mostra a figura a seguir.
a) Calcule a força exercida pela barra sobre o ombro de cada empregado.
b) Considere, agora, que E• esteja em repouso, apoiado sobre os dois pés, e com apenas um dos
baldes sobre a cabeça. A massa de E• é igual a 70 kg e a área de cada uma de suas botas é de 300
cm£. Determine a pressão exercida por ele sobre o chão.
14) Num posto fiscal de pesagem, um caminhão está em repouso sobre duas balanças, uma embaixo
de suas rodas dianteiras e a outra sob suas rodas traseiras. Ao fazer as leituras das balanças, o fiscal
verifica que a primeira marca 1,0 x 10¦N, mas percebe que a segunda está quebrada.
Profundo conhecedor de caminhões, o fiscal sabe que as distâncias entre o centro de massa C do
caminhão e os planos verticais que contêm os eixos dianteiro e traseiro das rodas valem,
respectivamente, d = 2,0 m e d‚ = 4,0 m, como ilustra a figura.
a) Calcule o peso do caminhão.
b) Determine a direção e o sentido da força que o caminhão exerce sobre a segunda balança e
calcule seu módulo.
15) As figuras mostram uma ginasta olímpica que se sustenta em duas argolas presas por meio de
duas cordas ideais a um suporte horizontal fixo; as cordas têm 2,0m de comprimento cada uma. Na
posição ilustrada na figura 1 os fios são paralelos e verticais. Nesse caso, as tensões em ambos os
fios valem T.
Na posição ilustrada na figura 2, os fios estão inclinados, formando o mesmo ângulo š com a vertical.
Nesse caso, as tensões em ambos os fios valem T' e a distância vertical de cada argola até o suporte
horizontal é h=1,80m, conforme indica a figura 2.
Sabendo que a ginasta pesa 540N, calcule T e T'.
GABARITO
1. a = 1,0 m/s£.
2. a) 0,60
b) 12,0N
3. (Ë3)/2
4. a) 0,5
b) 3.10¥ J
5. a) 40 m/s
b) 5,0 s
6. š = arc cos [2 . (h - r)/3r]
7. a) W(A) / W(B) = 1.
b) 8.000J, tanto para Abelardo, quanto para Heloísa.
8. 0,50 m¤/s.
9. h = L - Lcos 60 = 0,90.(1/2) = 0,45m
Considerando a energia potencial zero no ponto de equilíbrio no momento inicial temos
E(inicial) = mgh = 0,1.0,45.10 = 0,45J
E(final) = 0
|ÐE| = 0,45J
10. a) 80%
b) 4,7 × 10£ N
11. a)
T: Força elástica, causada pela (distensão da) mola
E: Empuxo, causado pela (pressão da) água
P: Peso, causado pela (atração gravitacional da) Terra
b) 7,0 cm.
c) 0,40 s.
12. 2 N
13. a) Força exercida ¸ 342,9 N
b) 1,5 N/cm£
14. a) 1,5x10¦N
b) 5x10¥N, na vertical para cima.
15. T = 270 N
T' = 300 N