r о ∆ )t(r)tt(rr о оо −∆+

32
Aula 19
17 CINEMÁTICA DE UMA PARTÍCULA
17.1 MOVIMENTO CURVILÍNEO
17.2 MOVIMENTO RETILÍNEO
17.3 MOVIMENTO CIRCUNFERENCIAL
18 CINEMÁTICA PLANAR DE UM CORPO RÍGIDO
18.1 TRANSLAÇÃO
18.2 ROTAÇÃO
18.3 MOVIMENTO PLANO GERAL ABSOLUTO
_______________________________________
17 CINEMÁTICA DE UMA PARTÍCULA
17.1 MOVIMENTO CURVILÍNEO
∆S
z
r ( t + ∆t )
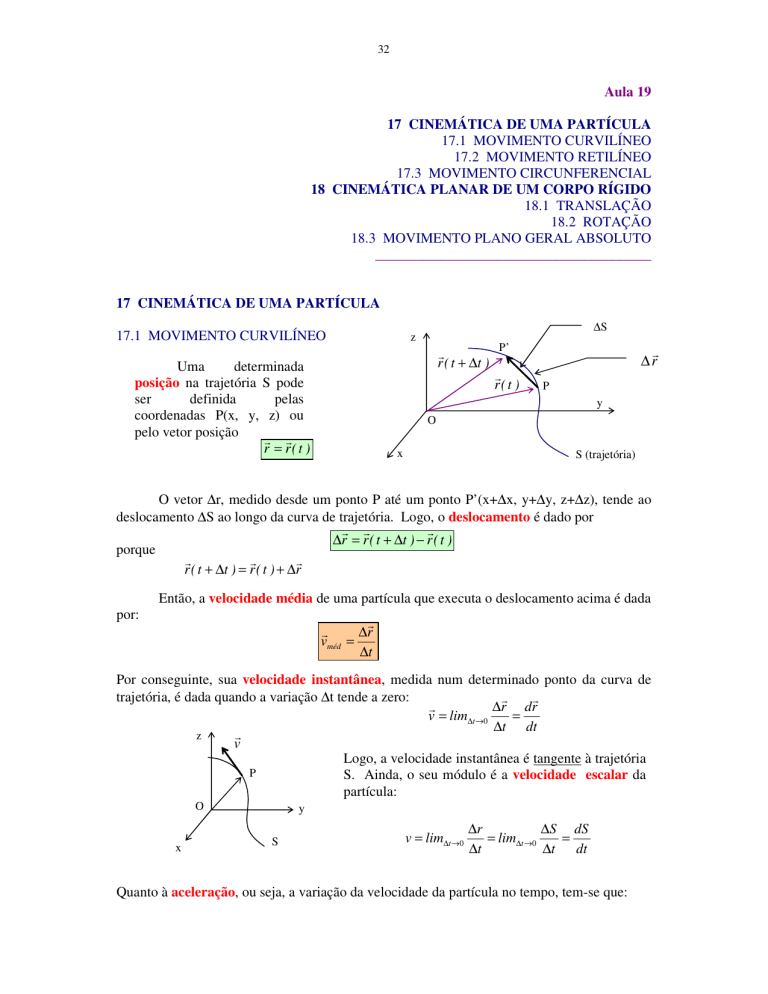
Uma
determinada
posição na trajetória S pode
ser
definida
pelas
coordenadas P(x, y, z) ou
pelo vetor posição
r = r( t )
P’
r( t )
∆r
P
y
O
x
S (trajetória)
O vetor ∆r, medido desde um ponto P até um ponto P’(x+∆x, y+∆y, z+∆z), tende ao
deslocamento ∆S ao longo da curva de trajetória. Logo, o deslocamento é dado por
∆r = r ( t + ∆t ) − r ( t )
porque
r ( t + ∆t ) = r ( t ) + ∆r
por:
Então, a velocidade média de uma partícula que executa o deslocamento acima é dada
vméd =
∆r
∆t
Por conseguinte, sua velocidade instantânea, medida num determinado ponto da curva de
trajetória, é dada quando a variação ∆t tende a zero:
∆r dr
v = lim∆t →0
=
∆t dt
z
v
Logo, a velocidade instantânea é tangente à trajetória
P
S. Ainda, o seu módulo é a velocidade escalar da
partícula:
O
x
y
S
v = lim∆t →0
∆r
∆S dS
= lim∆t →0
=
∆t
∆t dt
Quanto à aceleração, ou seja, a variação da velocidade da partícula no tempo, tem-se que:
33
améd =
v'
∆v
∆t
Aceleração instantânea:
v
P’
a = lim∆t →0
P
S
A grandeza vetorial aceleração possui um sentido que
aponta para dentro da curva da trajetória. Assim, duas
componentes, uma tangencial e outra normal, sempre
serão verificadas:
v2
dv
an =
at =
ρ
dt
at
a
P
an
∆v dv d 2 r
=
=
∆t dt dt 2
S
A componente tangencial da aceleração diz respeito à variação de intensidade do vetor
velocidade, enquanto que a componente normal (radial), à variação de sua direção. Seus
módulos estão correlacionados com o módulo da aceleração por:
a = at2 + an2
17.2 MOVIMENTO RETILÍNEO
Se, a partícula desenvolve uma trajetória retilínea (ρ = ∞, an = 0),
t
O
P
S
t+∆t
P’
∆S
tem-se que, escalarmente, para a posição S:
v=
Velocidade Instantânea:
Aceleração Instantânea:
dS
dt
dS
dt =
v
dv
dv
a=
dt =
dt
a
adS = vdv
Ainda, para o caso particular em que a aceleração é constante, tem-se que
Logo,
v
vo
t
dv = a dt
v = v 0 + at
v − v 0 = at
0
dv
= a = constante
dt
e
dS
= v = v 0 + at
dt
Portanto,
S
So
dS =
(v 0 + at )dt
0
t
S − S 0 = v0 t +
at 2
2
S = S 0 + v0 t +
at 2
2
Finalmente,
adS = vdv
a
S
So
dS =
v
v0
vdv
a( S − S 0 ) =
(
1 2
v − v 02
2
)
v 2 = v 02 + 2a ( S − S 0 )
34
17.3 MOVIMENTO CIRCUNFERENCIAL
dS
A velocidade angular ω e a aceleração angular
α, para ma trajetória que descreva uma circunferência
são dadas por:
dθ
ω=
dt
P’
dθ
O
dω d θ
α=
= 2
dt
dt
2
θ
r
S
P
A
Ainda, quando uma partícula percorre a trajetória circular, tem-se um movimento que
define uma velocidade escalar, uma aceleração tangencial e uma aceleração normal para o
ponto. Estas se correlacionam com as grandezas anteriores assim:
dS = rdθ
dS
dθ
=r
dt
dt
an =
v = rω
at =
v2 ω 2r 2
=
= rω 2
r
r
dv d (ωr )
dω
=
=r
= rα
dt
dt
dt
a t = rα
a n = rω 2
Da mesma forma, pode-se particularizar para a situação em que a aceleração angular
seja constante, resultando expressões semelhantes às encontradas anteriormente:
ω = ω 0 + αt
θ = θ 0 + ω 0t +
αt 2
ω 2 = ω 02 + 2α (θ − θ 0 )
2
18 CINEMÁTICA PLANAR DE UM CORPO RÍGIDO
18.1 TRANSLAÇÃO
Ocorre quando qualquer reta pertencente ao corpo conserva a mesma direção durante
o movimento. Ou seja, todos o pontos do corpo rígido em translação deslocam-se com a
mesma velocidade e aceleração.
z
rAB
rB
O
0
Velocidade:
B
vB = v A +
A
rA
drAB
dt
y
Aceleração:
x
aB = aA
Posição do ponto B:
rB = rA + rAB
vB = v A
35
18.2 ROTAÇÃO (EM TORNO DE UM EIXO FIXO)
Ocorre quando todas as partículas do corpo, exceto aquelas que estejam no eixo de
rotação, deslocam-se ao longo de trajetórias circulares. Para o corpo rígido a velocidade
angular e a aceleração angular de qualquer linha do corpo é sempre a mesma.
Rotação em torno de O: θ2 = θ1 + φ
y
Durante o movimento:
dθ 2 dθ 1 dφ
=
+
dt
dt
dt
B2
0
A2
θ2
φ
A1
Logo: ω = ω1 = ω2; α = α1 = α2
18.3 MOVIMENTO PLANO GERAL ABSOLUTO
É uma composição dos outros dois movimentos.
SG = r θ
G’
θ
r
SG = r θ
B
A
x’
x
O
G
B1
θ1
B’
vG =
dS G
dθ
=r
dt
dt
v G = rω
aG =
dv G
dω
=r
dt
dt
a G = rα