APSA 6 - Equações dos movimentos

FICHA DE TRABALHO DE FÍSICA E QUÍMICA A
NOVEMBRO 2011
___________________________________________________________________________________________________________________________________________
APSA Nº6
11º Ano de Escolaridade
1- Um móvel com movimento uniforme, parte de um ponto situado no semieixo positivo a 10m da
origem e passa por ela 5 s depois. A expressão analítica da lei do movimento no SI é:
A) x = 10 – 5 t
B) x = 10 – 2 t
C) x = 10 + 2 t
D) x = 10 + 5 t
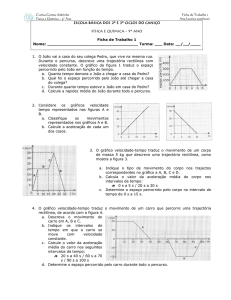
2- Dados os gráficos, x = f(t), diga para cada um deles o sentido do movimento do móvel.
3- O gráfico representa a posição em função do tempo, de dois carros A e B, que se deslocam numa
estrada rectilínea.
Podemos afirmar que a velocidade do carro A:
A – É menor que a do carro B.
B – É maior que a do carro B.
C – É igual à do carro B.
D – É crescente com o tempo.
E – É decrescente com o tempo.
4- Qual é a equação que representa o movimento de uma partícula, cujo gráfico do movimento está
representado na figura .
(A) x = 1 + t
(D) x = 1 – t
(B) x = t
(C) x = –1 + t
(E) x = –1 – t
1
Física e Química A
Ano Lectivo 2011/2012
5- Dois navios N e N partem do mesmo porto e deslocam-se sobre uma mesma recta com v =35 km/h
1
2
1
e v =25 km/h. A comunicação entre eles é possível, pela rádio, enquanto a distância entre eles não
2
ultrapassar 600 km. Determine o tempo durante o qual os dois navios comunicam entre si, admitindo
que os dois partem ao mesmo tempo e movem-se no mesmo sentido.
6- Conforme indica a figura, colocamos nas extremidades de um tubo de vidro, de 1,00 m de
comprimento, uma formiga e uma barata e deixamos uma ir ao encontro da outra. Verificamos que
os seus movimentos são aproximadamente uniformes e que elas se cruzam depois de 10 s, a 40 cm
da extremidade em que estava a formiga.
6.1- Qual é o gráfico que representa os movimentos anteriormente descritos?
6.2- Indique as velocidades da formiga e da barata.
6.3- Indique a expressão analítica da lei do movimento no SI da formiga e da barata.
6.4- Quando a barata chegar à outra extremidade do tubo, qual será a distância entre a formiga
e a barata.
7- Dois móveis A e B deslocam-se com movimento rectilíneo. As suas posições no decorrer do tempo
são dadas pelo seguinte gráfico da figura.
7.1- Escreva a expressão analítica da lei do movimento de cada
móvel.
7.2- Calcule o instante em que os dois móveis se encontram.
7.3- Calcule a coordenada de posição dos dois móveis no ponto
de encontro.
7.4- Construa um gráfico v = f (t) para o móvel B.
7.5- Calcule a partir do gráfico elaborado na alínea anterior o valor
do deslocamento do móvel B no intervalo [1,0; 2,0] s.
2
Física e Química A
Ano Lectivo 2011/2012
8- Um ponto material move-se ao longo de uma trajectória rectilínea, segundo a expressão analítica da
lei do movimento no SI:
2
x = -2 + 2t + t
8.1- Indique a posição inicial do ponto material, justificando o sinal algébrico.
8.2- Classifique o tipo de movimento do ponto material.
8.3- Determine o valor da aceleração do ponto material e represente o gráfico a = f(t).
8.4- Escreva a expressão analítica da lei das velocidades do ponto material.
8.5- Determine o valor da velocidade adquirida pelo ponto material após 5 s de movimento.
8.6- Calcule a distância percorrida pelo ponto material, após 3 s de movimento.
8.7- Que tempo demorou o ponto material a percorrer 24 m?
9- O gráfico da figura 1 representa a variação da velocidade, em função do tempo, de uma partícula
material, que se move numa trajectória rectilínea e que no instante t = 0 s se encontra na posição 4,0 m.
9.1- Classifique o movimento da partícula no intervalo de tempo [0;16]
s.
9.2- Trace o gráfico do valor da aceleração, em função do tempo,
correspondente ao intervalo de tempo [0;16] s.
9.3- Calcule o espaço percorrido pela partícula no intervalo [0;10] s.
9.4- Escreva expressão analítica da lei das velocidades do ponto
material
para o intervalo [6;10] s.
9.5- Indique um instante em que ocorre inversão no sentido do
movimento.
10- A tabela de dados refere-se a um móvel com movimento rectilíneo.
v (m/s)
t (s)
0
0
5
1
10
2
15
3
20
4
25
5
10.1- Determine o valor da aceleração do carro.
10.2- Escreva a expressão analítica da lei das velocidades.
10.3- Calcule o valor da velocidade do carro, decorridos 20 s de movimento.
11- O condutor de um automóvel desloca-se numa estrada rectilínea, com velocidade constante de
módulo 90 km/h durante 5 s. Após este instante, trava o veículo imobilizando-o em 3 s.
11.1- Trace o gráfico v = f(t) que descreve este movimento.
11.2- Calcule o valor da aceleração do carro durante a travagem.
3
Física e Química A
Ano Lectivo 2011/2012
11.3- Determine a distância percorrida durante a travagem.
11.4- Calcule a distância total percorrida até o carro parar.
12- Um automóvel, inicialmente em repouso num semáforo, iniciou o seu movimento percorrendo uma
trajectória rectilínea, quando surgiu a luz verde (fig. 2). Durante o percurso A aumentou
-1
uniformemente a velocidade, atingindo o valor de 30 m s , ao fim de 15 s de movimento. No percurso
B, a velocidade do automóvel manteve-se constante, durante 20 s.
Quando o condutor avistou o sinal vermelho reduziu uniformemente a velocidade do veículo,
efectuando o percurso C, até imobilizar o automóvel ao fim de 5 s. Calcule a distância que separa os
dois semáforos.
4
Física e Química A
Ano Lectivo 2011/2012
CORRECÇÃO
1. opção B;
é m.r.u., logo
t = 5s
t = 0s
x=0
x = 10 m
2. –positivo : A e C
, calcula-se v =
x = x0 + vt
Fica
parado (nulo) : B e F
x − x0
t − t0
v=
0 − 10
5−0
v = −2 m/s
x = 10 – 2t
negativo :DeE
3. opção C- É igual à do carro B. ( as duas rectas têm o mesmo declive )
4.
(C) x = –1 + t
parte da posição x = -1 e v= 1 m/s ( v = 0 – (-1) / 1 )
v1
5. v =35 km/h e v =25 km/h.
1
2
Aplica-se a lei do movimento a cada
barco
x1 = 35 t e x2 = 25 t
v2
Como não podem afastar-se mais de 600 Km
x1 – x2 = 600 ⇔
600 Km
35 t – 25 t = 600 ⇔ t = 60 h
66.1 Gráfico D.
6.2 t = 10 s
vf =
0,4
10
0
v f = 0,04 m / s
6.3 xf = 0,04 t
0,4 m
vb =
0,6
10
1m
v f = 0,06 m / s
xb = 1 – 0,06 t
6.4 quando a barata chegar à outra extremidade xb = 0
0 = 1 – 0,06 t
t = 16,7 s
Demora 16,7 s , nesse intervalo de tempo a formiga está na posição :xf = 0,04 x 16,7 xf = 0,67 m
Como a barata está na posição x = 0; ∆x = 0,67 m
77.1
Cálculo das velocidades v A =
Lei dos movimentos
7.2 Encontram-se quando xA = xB
10 − 8
= 2m / s
1
xA = 8 + 2t
8 + 2t = 5t
VB =
5
= 5m / s
1
xB = 5t
⇒
t = 2,67 s
7.3 Coordenadas do ponto onde se encontram ( t,x ) como xA = xB basta substituir em xB = 5 x 2,67
5
Física e Química A
Ano Lectivo 2011/2012
xB = 13,35 m
coordenadas (2,67 ; 13,35 )
⇒
7.4 e 7.5
∆x = área
v
(m/s)
∆x = (2 – 1) x 5
5
∆x = 5 m
0
1
8.
x = -2 + 2t + t 2
variado)
2
t (s)
8.1 x = -2 m
8.2 m.r.u.v. (movimento rectilíneo uniformemente
8.3 comparando com a expressão geral x = x0 + v0t + ½ at
8.4 v = 2 + 2t
8.6
8.5
v = 2+ 2x5
xfinal = -2 + 2x3 + 3 2
2
verifica-se que ½ a = 1 ⇒ a = 2 m/s2
v = 12 m/s
-2
d = ∆ x1 + ∆ x2
8.7
∆ x =24 m
d = 0 – (-2) + 13-0
∆ x = 2t + t 2
∆x2
∆x1
xfinal = 13 m
0
13
d = 15m
24 = 2t + t 2
equação de 2º grau t 2 + 2t – 24 = 0
pela fórmula resolvente t = − 6,0 s ( valor sem significado em física) e t = 4.0 s ( valor válido)
9.1 Desloca-se no sentido positivo da trajectória,
9.2
durante 8 s, a velocidade aumenta até t = 4s
e mantém-se durante 2s; depois diminui de
velocidade até t = 8 s, quando inverte o sentido
do movimento passando a movimentar-se em
sentido negativo.
a
m/s2
12
6
3
0
De 8 a 14 s desloca-se em sentido negativo.
A velocidade aumenta de 8 a 10s,
2
4
6
8
10 12 14
t (s)
-6
pára de 10 a 12s e diminui até t=14s e fica em repouso
9.3 O espaço percorrido pela partícula no intervalo [0;10] s é igual à área nesse intervalo de tempo.
A total = A1 + A2 + A3 + A4
Atotal =
4 × 12
2 × 12
− 12 × 2
+ 2 x12 +
+(
)
2
2
2
1
2
3
4
A total = 24 + 24 + 12 +12
A total = 72
O espaço percorrido pela partícula no intervalo [0;10] s é 72 m
6
Física e Química A
Ano Lectivo 2011/2012
9.4 Para saber a expressão analítica da lei das velocidades do ponto material para o intervalo [6;10] s
temos
v = v0 + at
v0 = 12 m/s
a=
e
a lei das velocidades fica:
v f − v0
∆t
10.1. O valor da aceleração do carro é dada por a =
calcular-se a aceleração a =
25 − 0
5−0
∆v
por qualquer intervalo considerado pode
∆t
a = 5 m / s2
v = 5t logo v = 5x20
v = 100 m/s
11.1.
m.r.u.
v = 90 km/h = 25 m/s
t=5s
a=
0 − 25
8−5
a = −6 m / s 2
x=5t
10.3. A lei das velocidades é
11.2.
− 12 − 12
10 − 6
v = 12 – 6t
9.5 Inverte o sentido do movimento em t = 8s
10.2. Como é m.r.u.a., fica
a=
v
(m/s)
m.r.u.r
v=0
t=3s
25
a = 8,33 m / s 2
0
1
2
3
4
5
6
7
8 t (s)
11.3. distância percorrida = área
distância percorrida =
(8 − 5) × 25 = 37,5 m
2
11.4. distância total percorrida = 5x25 + 37,5 distância total percorrida = 162,5 m
12. Traduzindo o enunciado num eixo de referência:
m.r.u.a.
v0 = 0
t0 = 0
m.r.u.
m.r.u.r.
v = 30
t = 15s
v = 30
t = 35s
1ª parte( m.r.u.a.)
2ª parte(m.r.u.)
x = ½ at 2
x = x0 + vt
x = x0 + v0t + ½ at
x = 225 + 30x20
a=
a=
30
= 2m / s2
15
x1 = ½ 2x(15) 2 = 225 m
x2 = 825m
v=0
t = 40s
3ª parte( m.r.u.r.)
2
0 − 30
= − 6m / s2
40 − 35
x3 = 825 + 30x5 -3x5 2 = 900 m
7
Física e Química A
Ano Lectivo 2011/2012
Como parte de x = 0 e chega a x = 900 m ; então os dois semáforos distam 900 m.
8
Física e Química A
Ano Lectivo 2011/2012