(A) Interacção de RX com a matéria

10/6/2014
Revisão de Conceitos e Fundamentos de
Física das Radiações (A)
Augusto Oliveira – [email protected]
PSR - WP4 ARIAS
2014
Interacção de RX com a matéria
a.
b.
c.
d.
e.
f.
g.
Interacções físicas
Secção eficaz
Interacções com a matéria
Atenuação
Coeficientes de interacção
Exercício
Roteiro para a secção eficaz
Incident
Radiation
beam
PSR – WP4 ARIAS – [email protected]
2
1
10/6/2014
Interacção de RX com a matéria
Interacções físicas
PSR – WP4 ARIAS – [email protected]
3
Interacção de RX com a matéria
Interacções físicas
PSR – WP4 ARIAS – [email protected]
4
2
10/6/2014
Interacção de RX com a matéria
Interacções físicas
Dominância da
produção de pares
Dominância do efeito
fotoeléctrico
Dominância do efeito
de Compton
PSR – WP4 ARIAS – [email protected]
5
Interacção de RX com a matéria
Interacções físicas
PSR – WP4 ARIAS – [email protected]
6
3
10/6/2014
Interacção de RX com a matéria
Secção eficaz
PSR – WP4 ARIAS – [email protected]
x
dx
7
Interacção de RX com a matéria
Secção eficaz
PSR – WP4 ARIAS – [email protected]
dx
8
4
10/6/2014
Interacção de RX com a matéria
Secção eficaz
Número total de
centros de dispersão
na camada dx é:
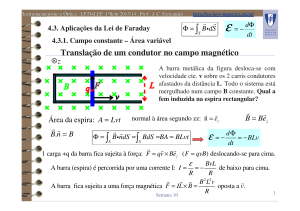
Consideremos uma lâmina de
determinado material onde existem
N centros de dispersão por
unidade de volume
N A dx
A
Por cada centro de
dispersão existe uma
área eficaz de colisão:
s = p R2
2R
A área total de colisão,
para a camada dx é:
N A s dx
dx
PSR – WP4 ARIAS – [email protected]
9
Interacção de RX com a matéria
Secção eficaz
A área total de colisão, para a camada dx é:
N A s dx
A
dw 
área total de colisão
área frontal
dw 
NAsdx
 Nsdx
A
R
dw
 Ns
dx
dx
PSR – WP4 ARIAS – [email protected]
10
5
10/6/2014
Interacção de RX com a matéria
Secção eficaz
s – secção eficaz
dw
 Ns
dx
mNs
Probabilidade de ocorrência de um dado processo.
– coeficiente linear de atenuação
N – Número de átomos por unidade de volume [m -3]
s – unidade de área [m2]
Então m tem unidades [m-1]
1
l
 Ns
l – percurso livre médio, valor médio do espaço
percorrido pela partícula entre duas colisões
sucessivas [m].
PSR – WP4 ARIAS – [email protected]
11
Interacção de RX com a matéria
Interacções com a matéria
PSR – WP4 ARIAS – [email protected]
12
6
10/6/2014
Interacção de RX com a matéria
Atenuação
dn  - m ndx
dn
 - mdx
n
ln n  -mx  ln C
n  C exp( -mx)
( x  0),
n
n-dn
n0  C exp(0)  C
n  n0 exp( -mx)
dx
PSR – WP4 ARIAS – [email protected]
13
Interacção de RX com a matéria
Coeficientes de interacção
m  s C s coh 
 


  


[m2 kg-1]
mtr
s


 f  f C C  f




[m2 kg-1]
Os pesos (f) são factores de conversão que indicam, para a respectiva interacção, a fracção de energia dos
fotões que eventualmente é convertida em energia cinética dos electrões e é dissipada no meio através de
perdas em colisões, ionização e excitação.
men mtr
1 - g 



[m2 kg-1]
onde g é a fracção de energia dos electrões que é emitida como bremsstrahlung.
PSR – WP4 ARIAS – [email protected]
14
7
10/6/2014
Interacção de RX com a matéria
Exercício
Exercício:
Considere um feixe de radiação incidente num material de espessura x
caracterizado pelo coeficiente de atenuação m.
Determine qual é a fracção de fotões retirados do feixe primário (fotões
secundários), em função da espessura do material e do coeficiente de atenuação.
N
m
N(0)
E
N
N(0)
?
E
x
PSR – WP4 ARIAS – [email protected]
15
Interacção de RX com a matéria
Roteiro para a secção eficaz
Nas equações de Maxwell
1831 – 1879 (48 anos)
Intervêm o campo eléctrico, E, e o campo magnético, B, que são expressos em
termos do potencial vectorial, A, e escalar, 
𝐵 = 𝛻 × 𝐴(𝑟, 𝑡)
𝐸=−
1 𝜕𝐴(𝑟 , 𝑡)
− 𝛻𝜙(𝑟 , 𝑡)
𝑐 𝜕𝑡
PSR – WP4 ARIAS – [email protected]
16
8
10/6/2014
Interacção de RX com a matéria
Roteiro para a secção eficaz
Na descrição hamiltoniana, o hamiltoniano
𝐻=
𝑝2
2𝑚
1805 – 1865 (60 anos)
Considerando o electromagnetismo, leva à equação de Schrodinger:
𝑖ℏ
𝜕𝜓
ℏ2 2 𝑖𝑒ℏ
𝑒2
= −
𝛻 +
𝐴∙𝛻+
𝐴2 + 𝑉 𝜓
𝜕𝑡
2𝑚
𝑚𝑐
2𝑚𝑐 2
1887 – 1961 (73 anos)
PSR – WP4 ARIAS – [email protected]
17
Interacção de RX com a matéria
Roteiro para a secção eficaz
•
•
•
•
•
•
•
O potencial vector, A, é decomposto em série de Fourier e osciladores de radiação
expressos em termos de operadores de criação e aniquilação.
Na segunda quantização definem-se operadores de criação e aniquilação.
O operador de criação cria 1 fotão num determinado estado.
O operador de aniquilação destrói ou aniquila 1 fotão num determinado estado.
O hamiltoniano do sistema radiação mais matéria é expresso como a soma de um termo
independente do tempo e um termo de perturbação, com o objectivo de se aplicar a teoria
das perturbações.
Define-se a função de estado do sistema radiação + matéria.
Antes da interacção o átomo e o fotão estão em determinados estados definidos e a
equação de Schrodinger conduz ao cálculo da secção eficaz recorrendo principalmente a
três aproximações:
•
•
•
Aproximação de Waller-Hartree (na dispersão inelástica a energia do fotão não é muito alterada
durante a interacção).
Aproximação de impulso (assume-se que a interacção entre o campo de radiação e o electrão
atómico tem lugar num tempo tão curto que o potencial em que o electrão se move é constante).
Aproximação de estado excitado (Na dispersão inelástica o fotão incidente fornece alguma
energia a um electrão atómico o qual é levado de um estado atómico para um estado excitado. Os
electrões passivos permanecem nos seus estados iniciais).
PSR – WP4 ARIAS – [email protected]
18
9
10/6/2014
PSR – WP4 ARIAS – [email protected]
19
10