1. a) O choque é elástico, o que significa que há conservação do

Série 7
1.
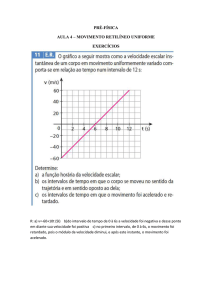
a) O choque é elástico, o que significa que há conservação do momento linear
(energia inicial de A vai ser energia final de C) e da energia total do sistema,
∆𝐸𝑚 = 0, uma vez que não actuam forças exteriores.
Assim, 𝐸𝑝inicial = 𝐸𝑐final que o pêndulo C atinge a altura H.
b) Os pêndulos A e B após o choque param.
Toda a energia do pêndulo A é transferido para o B pois conserva-se o
momento linear, e ambos os pêndulos tem a mesma massa. Uma vez que o
choque entre B e C também é elástico, toda a energia de B passa para C, sendo
a velocidade de B após o choque igual à sua velocidade antes do choque e
igual à velocidade de A após o choque (= 0).
c) ∆𝐸𝑚 = 0
𝐸𝑝inicial = 𝐸𝑐final
𝑣A =
2𝑔ℎ1 (𝑣 A = 𝑣 final de A).
Numa colisão completamente inelástica conserva-se o momento linear mas
não a energia total:
𝑝 = 𝑚𝑣, 𝑝inicial = 𝑝final
𝑚A × 𝑣A + 0 = (𝑚A + 𝑚B + 𝑚C) × 𝑣f
 𝑣f =
2𝑔ℎ1
3
m/s
Após o choque já há conservação da energia total do sistema, logo:
1
𝑚
2
𝑣 f 2 = 𝑚𝑔ℎ2

1
2𝑔ℎ1
𝑚
2
9

ℎ1
9
= ℎ2
= 𝑚𝑔ℎ2
Série 7
2.
a) Estaria incorrecto dizer à partida que não há forças exteriores a actuar no
vagão e por isso o momento linear conservava-se.
Na verdade, apenas existe conservação do momento linear em x porque a sua
força resultante é nula (Frx=0). Se considerarmos o sistema vagão com areia,
Frx=0 porque todas as outras forças que actuam no sistema passam a ser
forças interiores, pares acção-reacção que se anulam dois a dois, conservandose assim o momento linear.
Em y existem forças a actuar mas não interessam para a resolução do
exercício.
Um choque completamente inelástico caracteriza-se pela conservação do
momento linear e pela não conservação da energia total do sistema. Sendo a
velocidade final do conjunto (𝑣 c) só uma:
𝑝 = 𝑚𝑣, 𝑝inicial = 𝑝final
mareia × 0 + mvagão × 7 = (mareia + mvagão) × 𝑣 c
 𝑣 c = 5 m/s
b) Depois o vagão começa a perder areia através de um tubo vertical. A areia
acelera segundo y, mas não interessa para o exercício, uma vez que
consideramos apenas o movimento segundo x.
A velocidade em x da areia (𝑣) é exactamente a mesma velocidade que o
vagão em x, vagão este que continua o seu movimento com velocidade
constante de 5m/s. (mareia que resta = 100Kg = mareia que caiu).
Por isso:
(mareia + mvagão) × 5 = (mareia que resta + mvagão) × 𝑣 + mareia que caiu × 𝑣
 𝑣 = 5m/s