Fís. Semana 9 Leonardo Gomes (Guilherme Brigagão)

Fís.
Este conteúdo pertence ao Descomplica. Está vedada a
cópia ou a reprodução não autorizada previamente e por
escrito. Todos os direitos reservados.
Semana 9
Leonardo Gomes
(Guilherme Brigagão)
CRONOGRAMA
03/04
Principais forças da
dinâmica
18:00
05/04
10/04
Principais forças da
Exercícios de leis
dinâmica
de Newton
08:00
11:00
18:00
Decomposição
de forças e plano
inclinado
18:00
12/04
Decomposição
Exercícios de
de forças e plano
decomposição
inclinado
de forças e plano
inclinado
08:00
11:00
18:00
19/04
Força de atrito
Exercícios de força
de atrito
08:00
24/04
11:00
18:00
Forças em
trajetórias
curvilíneas
18:00
26/04
Forças em
Trabalho de uma
trajetórias
força
curvilíneas
08:00
17/04
Força de atrito
18:00
11:00
18:00
12
abr
Exercícios
de decomposição de forças e
plano inclinado
01. Resumo
02. Exercícios de Aula
03. Exercícios de Casa
04. Questão Contexto
RESUMO
Toda grandeza vetorial pode ser decomposta em
Plano Inclinado
componentes ortogonais X e Y. Funciona exatamente da mesma forma com que fazíamos na velocidade
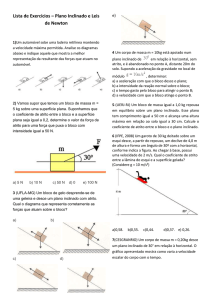
Considere um bloco deslizando num plano θ incli-
inicial do lançamento oblíquo, o vetor forma um ân-
nado, sem atrito, que forma um ângulo com a hori-
gulo com uma direção de referência (no lançamen-
zontal. Note que, ao marcar as forças peso e normal,
to oblíquo era o solo) e aplicávamos seno e cosseno
elas não se anulam.
para determinar a velocidade na vertical e na horizontal.
Usamos um referencial XY inclinado em relação à
horizontal e com o X na direção do movimento e fa-
Para fazer a decomposição, utilizaremos sempre o
zemos a decomposição da força peso nas compo-
triângulo:
nentes X e Y do novo referencial.
Como não existe movimento na direção Y do referencial, podemos afirmar que a força normal se anula com a componente Y do peso. Note também que
no eixo X haverá uma força resultante que atua no
Podemos escrever então:
N=P y = Pcos θ
27
bloco, a componente X do peso.
Importante!
Podemos definir então
sen(a)=a/b
cos(a)=c/b
tg(a)=a/c
O ângulo entre o plano inclinado e a horizontal é o
mesmo ângulo que a vertical e a reta perpendicular
ao plano inclinado. De acordo com o desenho acima, o ângulo θ do plano inclinado com a horizontal é
o mesmo que o eixo X e a força peso.
Fís.
FR=P x=Psen θ
EXERCÍCIOS DE AULA
1.
A figura abaixo mostra um corpo I de massa mI=2 kg apoiado em um plano inclinado e amarrado a uma corda, que passa por uma roldana e sustenta um outro
corpo II de massa mII=3 kg.
Despreze a massa da corda e atritos de qualquer natureza.
a) Esboce o diagrama de forças para cada um dos dois corpos.
b) Se o corpo II move-se para baixo com aceleração a=4 m/s², determine a tra-
28
ção T na corda.
zer uma aplicação prática do assunto: analisar o que ocorre com ele e sua tábua
de morro (usada no “esquibunda”), ao descer uma duna, inclinada de 30° em relação à horizontal e cuja extensão é de 40 m. Inicialmente, Paulinho passa numa
farmácia e verifica que a massa total, mT, do conjunto (isto é, sua massa mais a
massa da tábua) é de 60 kg. Sendo a tábua de fórmica, bastante lisa e lubrificada
com parafina, ele decide, numa primeira aproximação, desprezar o atrito entre
a tábua e a areia da duna bem como a resistência do ar. Admitindo que, em nenhum momento da descida, Paulinho coloca os pés em contato com a areia, considerando que a aceleração da gravidade é 10 m/s² e lembrando que sen30°=0,5:
a) determine a velocidade, em m/s e em km/h, com que o conjunto (Paulinho
com a tábua) chegará à base da duna, supondo que ele tenha partido, do topo,
do estado de repouso;
b) reproduza a figura abaixo e faça o diagrama das forças externas que atuam no
conjunto, colocando essas forças no centro de massa do bloco; (Observe que,
na figura, o bloco representa o conjunto, e o plano inclinado representa a duna.)
c) calcule o valor da força resultante que atua no conjunto;
Fís.
2.
Paulinho, após ter assistido a uma aula de Física sobre plano inclinado, decide fa-
3.
Um plano inclinado faz um ângulo de 30° com a horizontal. Determine a força
constante que, aplicada a um bloco de 50 kg, paralelamente ao plano, faz com
que ele deslize (g =10 m/s²):
I – para cima, com aceleração de 1,2 m/s²;
II – para baixo, com a mesma aceleração de 1,2 m/s².
Despreze o atrito do bloco com o plano.
a) I) 310 N para cima; II) 190 N para cima
b) I) 310 N para cima; II) 310 N para baixo
c) I) 499 N para cima; II) 373 N para cima
d) I) 433 N para cima; II) 60 N para cima
e) I) 310 N para cima; II) 190 N para baixo
Num local onde a aceleração gravitacional tem módulo 10 m/s², dispõe-se o condições, a intensidade da força que o bloco A exerce no bloco B é:
29
junto abaixo, no qual o atrito é desprezível, a polia e o fio são ideais. Nestas con-
Fís.
4.
a) 20 N
b) 32 N
c) 36 N
d) 72 N
e) 80 N
5.
Um plano está inclinado, em relação à horizontal, de um ângulo θ cujo seno é
igual a 0,6 (o ângulo é menor do que 45°). Um bloco de massa m sobe nesse plano inclinado sob a ação de uma forca horizontal F, de módulo exatamente igual
ao módulo de seu peso, como indica a figura a seguir.
Supondo que não haja atrito entre o bloco e o plano inclinado, calcule o módulo
Deseja-se manter um bloco em repouso sobre um plano inclinado 30° com a horizontal. Para isso, como os atritos entre o bloco e o plano inclinado são desprezíveis, é necessário aplicar sobre o bloco uma força. Numa primeira experiência,
mantém-se o bloco em repouso aplicando uma força horizontal F, cujo sentido
está indicado na figura 1.
Numa segunda experiência, mantém-se o bloco em repouso aplicando uma força F paralela ao plano inclinado, cujo sentido está indicado na figura 2.
Calcule a razão de |F’|/|F|.
Fís.
6.
30
da aceleração do bloco. Adote g = 10m/s².
7.
A figura a seguir mostra um corpo de massa 50kg sobre um plano inclinado sem
atrito, que forma um ângulo é com a horizontal. A intensidade da força F que fará
o corpo subir o plano com aceleração constante de 2 m/s² é:
Dados: g=10m/s²; sen θ =0,6
a) 50 N
b) 100 N
c) 200 N
d) 300 N
EXERCÍCIOS PARA CASA
1.
Duas pequenas esferas de aço são abandonadas a uma mesma altura h do solo.
A esfera (1) cai verticalmente. A esfera (2) desce uma rampa inclinada 30° com a
horizontal, como mostra a figura.
Considerando os atritos desprezíveis, calcule a razão t1/t2 entre os tempos gastos pelas esferas (1) e (2), respectivamente, para chegarem ao solo.
Fís.
31
e) 400 N
2.
É dado um plano inclinado de 10m de comprimento e 5m de altura, conforme é
mostrado na figura. Uma caixa, com velocidade inicial nula, escorrega, sem atrito, sobre o plano. Se g=10 m/s², o tempo empregado pela caixa para percorrer
todo o comprimento do plano, é:
a) 5 s
b) 3 s
c) 4 s
No sistema mostrado, o fio e a polia e o atrito entre as superfícies em contato é
desprezível. Abandonando-se o corpo B a partir do repouso, no ponto M, verifica-se que, após 2s, ele passa pelo ponto N com velocidade de 8 m/s. Sabendo-se que a massa do corpo A é de 5 kg, a massa do corpo B é
a) 1 kg
b) 2 kg
c) 3 kg
d) 4 kg
e) 5 kg
Fís.
3.
32
d) 2 s
lho ilustrado abaixo, desde o ponto A até o ponto E, sem perder contato com o
mesmo. Desprezam-se as forças de atrito. Em relação ao trilho, o gráfico que
melhor representa a aceleração escalar da partícula em função da distância percorrida é:
33
a)
b)
c)
d)
e)
Fís.
4.
Uma partícula de massa m desliza com movimento progressivo ao longo do tri-
5.
Um bloco desliza, sem atrito, sobre um plano inclinado de um ângulo a, conforme mostra a figura a seguir.
Considerando-se x a abscissa de P num instante genérico t e sabendo-se que o
bloco partiu do repouso em x=0 e t=0, pode-se afirmar que:
a) x=(1/4)gt².sen(2 a)
b) x=(1/2)gt².sen(a)
c) x=(1/4)gt².cos(a)
34
6.
e) x=(1/2)gt².sen(2a)
Uma esfera desce um plano inclinado sem atrito. Ao percorrer determinada dis-
Fís.
d) x=(1/2)gt².cos(2a)
tância, sua velocidade passa de 12m/s para 28m/s, em 5,0s. O ângulo que mede
a inclinação da rampa é tal que possui: (Dado: g = 10 m/s²)
a) seno igual a 0,32.
b) tangente igual a 1,36.
c) cosseno igual a 0,50.
d) seno igual a 0,87.
e) cosseno igual a 0,28.
QUESTÃO CONTEXTO
Um corpo de massa m desliza sem atrito sobre a superfície plana (e inclinada
de um ângulo á em relação à horizontal) de um bloco de massa M sob à ação da
mola, mostrada na figura. Esta mola, de constante elástica k e comprimento natural C, tem suas extremidades respectivamente fixadas ao corpo de massa m e
ao bloco. Por sua vez, o bloco pode deslizar sem atrito sobre a superfície plana
e horizontal em que se apoia. O corpo é puxado até uma posição em que a mola
seja distendida elasticamente a um comprimento L(L>C), tal que, ao ser liberado, o corpo passa pela posição em que a força elástica é nula. Nessa posição o
Fís.
35
módulo da velocidade do bloco é
GABARITO
01.
Exercícios para aula
1.
b) T=18N
2.
a) 20 m/s = 72 km/h; c) 300 N; d) menor
03.
Questão contexto
3.a
4.b
5.2,0m/s²
6.√3/2
7.e
02.
Exercícios para casa
1.
t1/t2 = ½
2.d
3.c
6.a
Fís.
5.a
36
4.a