Lentes - Webnode

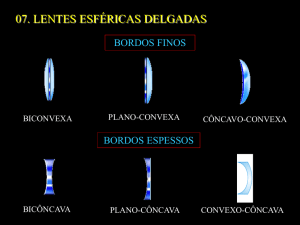
Lentes
Parte I
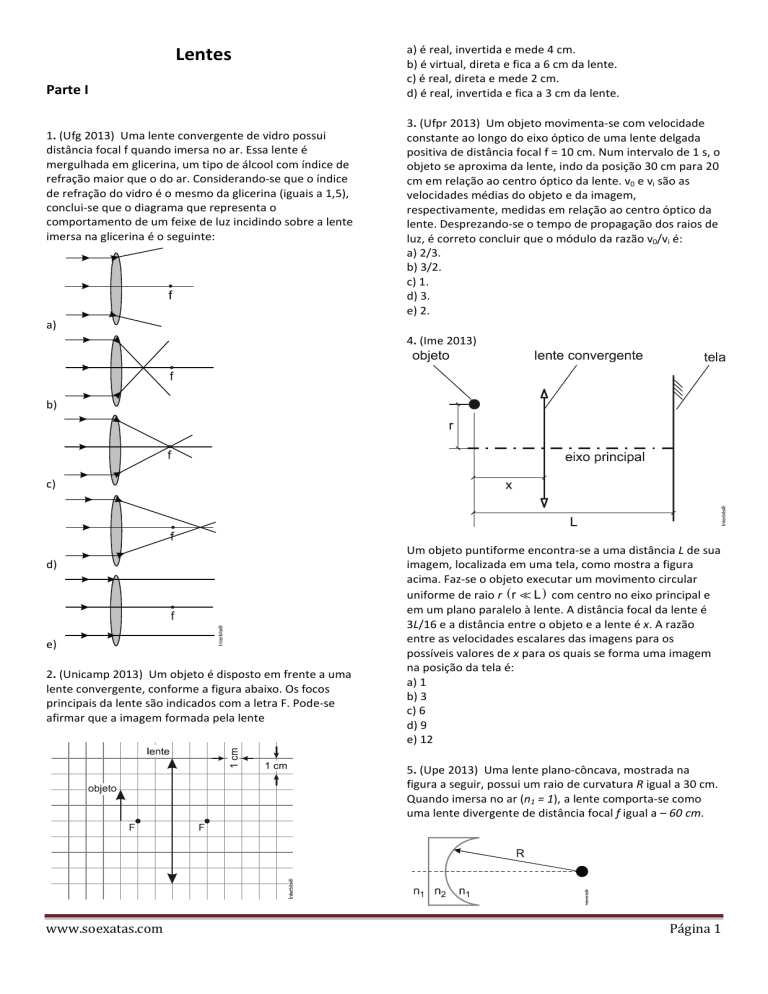
1. (Ufg 2013) Uma lente convergente de vidro possui
distância focal f quando imersa no ar. Essa lente é
mergulhada em glicerina, um tipo de álcool com índice de
refração maior que o do ar. Considerando-se que o índice
de refração do vidro é o mesmo da glicerina (iguais a 1,5),
conclui-se que o diagrama que representa o
comportamento de um feixe de luz incidindo sobre a lente
imersa na glicerina é o seguinte:
a) é real, invertida e mede 4 cm.
b) é virtual, direta e fica a 6 cm da lente.
c) é real, direta e mede 2 cm.
d) é real, invertida e fica a 3 cm da lente.
3. (Ufpr 2013) Um objeto movimenta-se com velocidade
constante ao longo do eixo óptico de uma lente delgada
positiva de distância focal f = 10 cm. Num intervalo de 1 s, o
objeto se aproxima da lente, indo da posição 30 cm para 20
cm em relação ao centro óptico da lente. v0 e vi são as
velocidades médias do objeto e da imagem,
respectivamente, medidas em relação ao centro óptico da
lente. Desprezando-se o tempo de propagação dos raios de
luz, é correto concluir que o módulo da razão v0/vi é:
a) 2/3.
b) 3/2.
c) 1.
d) 3.
e) 2.
a)
4. (Ime 2013)
b)
c)
d)
e)
2. (Unicamp 2013) Um objeto é disposto em frente a uma
lente convergente, conforme a figura abaixo. Os focos
principais da lente são indicados com a letra F. Pode-se
afirmar que a imagem formada pela lente
Um objeto puntiforme encontra-se a uma distância L de sua
imagem, localizada em uma tela, como mostra a figura
acima. Faz-se o objeto executar um movimento circular
uniforme de raio r ( r ≪ L ) com centro no eixo principal e
em um plano paralelo à lente. A distância focal da lente é
3L/16 e a distância entre o objeto e a lente é x. A razão
entre as velocidades escalares das imagens para os
possíveis valores de x para os quais se forma uma imagem
na posição da tela é:
a) 1
b) 3
c) 6
d) 9
e) 12
5. (Upe 2013) Uma lente plano-côncava, mostrada na
figura a seguir, possui um raio de curvatura R igual a 30 cm.
Quando imersa no ar (n1 = 1), a lente comporta-se como
uma lente divergente de distância focal f igual a – 60 cm.
www.soexatas.com
Página 1
Assinale a alternativa que corresponde ao índice de
refração n2 dessa lente.
a) 0,5
b) 1
c) 1,5
d) 2
e) 2,5
c) real, direita e maior que o objeto.
d) virtual, direita e maior que o objeto.
e) real, invertida e maior que o objeto.
10. (Epcar (Afa) 2012) A figura 1 abaixo ilustra o que um
observador visualiza quando este coloca uma lente delgada
côncavo-convexa a uma distância d sobre uma folha de
papel onde está escrita a palavra LENTE.
6. (Ufpr 2013) Um estudante possui uma lente convergente
cujos raios de curvatura de ambas as superfícies são iguais
a 30 cm. Ele determinou experimentalmente a distância
focal da lente no ar e obteve o valor de 10 cm. Com essas
informações, é possível determinar o índice de refração da
lente e assim saber de qual material ela foi feita.
a) Com base nessas informações, calcule o índice de
refração da lente.
b) Se o estudante determinasse a distância focal com a
lente imersa na água, ele obteria o mesmo valor descrito
no enunciado? Justifique a sua resposta.
7. (G1 - ifpe 2012) Analisando os três raios notáveis de
lentes esféricas convergentes, dispostas pelas figuras
abaixo, podemos afirmar que:
a) Apenas um raio está correto.
b) Apenas dois raios são corretos.
c) Os três raios são corretos.
d) Os raios notáveis dependem da posição do objeto, em
relação ao eixo principal.
e) Os raios notáveis dependem da posição da lente, em
relação ao eixo principal.
8. (Ucs 2012) Pela teoria da Relatividade Geral de Einstein,
quando raios de luz provenientes de um corpo estelar,
como estrelas ou galáxias, passam muito próximos de um
objeto estelar de grande densidade de massa, esses raios
de luz são desviados para um ponto de encontro oposto ao
lado em que os raios incidem no objeto. No contexto da
ótica, esse objeto de grande densidade de massa estaria
fazendo o papel de
a) um espelho plano.
b) um filtro polarizador.
c) uma lente.
d) um espelho côncavo.
e) um espelho convexo.
9. (Espcex (Aman) 2012) Um objeto é colocado sobre o
eixo principal de uma lente esférica delgada convergente a
70 cm de distância do centro óptico. A lente possui uma
distância focal igual a 80 cm. Baseado nas informações
anteriores, podemos afirmar que a imagem formada por
esta lente é:
a) real, invertida e menor que o objeto.
b) virtual, direita e menor que o objeto.
www.soexatas.com
Justapondo-se uma outra lente delgada à primeira,
mantendo esta associação à mesma distância d da folha, o
observador passa a enxergar, da mesma posição, uma nova
imagem, duas vezes menor, como mostra a figura 2.
Considerando que o observador e as lentes estão imersos
em ar, são feitas as seguintes afirmativas.
I. A primeira lente é convergente.
II. A segunda lente pode ser uma lente plano-côncava.
III. Quando as duas lentes estão justapostas, a distância
focal da lente equivalente é menor do que a distância
focal da primeira lente.
São corretas apenas
a) I e II apenas.
b) I e III apenas.
c) II e III apenas.
d) I, II e III.
11. (Ufpr 2012) Um datiloscopista munido de uma lupa
analisa uma impressão digital. Sua lupa é constituída por
uma lente convergente com distância focal de 10 cm. Ao
utilizá-la, ele vê a imagem virtual da impressão digital
aumentada de 10 vezes em relação ao tamanho real. Com
base nesses dados, assinale a alternativa correta para a
distância que separa a lupa da impressão digital.
a) 9,0 cm.
b) 20,0 cm.
c) 10,0 cm.
d) 15,0 cm.
e) 5,0 cm.
Página 2
12. (Uesc 2011)
1. Trace no diagrama, até a região à direita da segunda
lente, a continuação dos dois raios de luz e indique a
posição dos dois focos de cada uma das lentes.
2. Determine o diâmetro do feixe de luz à direita da
segunda lente em função de d e das distâncias focais
f1 e f2 das lentes.
14. (Ufsm 2011) Na figura a seguir, são representados um
objeto (O) e a sua imagem (I) formada pelos raios de luz
A análise da figura que representa o esquema de formação
de imagens em um microscópio composto, um instrumento
óptico que possui componentes básicos que são duas
lentes, a objetiva e a ocular, que permitem a observação de
pequenos objetos com bastante ampliação, permite
afirmar:
a) A lente objetiva e a ocular possuem bordas grossas.
b) A imagem A’B’, em relação à ocular, é um objeto virtual.
c) A imagem formada pelo microscópio, A’’B’’, é virtual em
relação à objetiva.
d) O valor absoluto da razão entre y’’ e y é a ampliação
fornecida pelo microscópio.
e) A distância entre a objetiva e a ocular é igual à soma das
distâncias focais das lentes objetiva e ocular.
13. (Ufmg 2011) Em um laboratório de óptica, Oscar
precisa aumentar o diâmetro do feixe de luz de um laser.
Para isso, ele prepara um arranjo experimental com duas
lentes convergentes, que são dispostas de maneira que
fiquem paralelas, com o eixo de uma coincidindo com o
eixo da outra. Ao ligar-se o laser, o feixe de luz é alinhado
ao eixo do arranjo.
Esse arranjo está representado neste diagrama:
Nesse diagrama, as duas linhas horizontais com setas
representam dois raios de luz do feixe. O diâmetro do feixe
é indicado pela letra d. A linha tracejada horizontal
representa o eixo das duas lentes.
O feixe de luz, que incide nesse arranjo, atravessa-o e sai
dele alargado, na mesma direção de incidência.
Considerando essas informações,
www.soexatas.com
Assinale a alternativa que completa corretamente as
lacunas.
A lente em questão é _________________, porque , para
um objeto real, a imagem é _________ e
aparece________________ que o objeto.
a) convergente - real - menor
b) convergente - virtual - menor
c) convergente - real - maior
d) divergente - real - maior
e) divergente - virtual - menor
15. (Upe 2011) A figura a seguir apresenta um objeto real o
e sua imagem i produzida por uma lente delgada. Considere
f como sendo a distância focal entre o centro óptico da
lente O e o foco principal objeto F.
Analise as afirmações a seguir e conclua.
( ) A imagem é real, invertida e menor, e o centro óptico
O encontra-se no eixo principal, a 3cm à esquerda da
imagem i.
( ) A imagem é real, invertida e menor, e o foco principal
objeto F encontra-se no eixo principal, a 8cm à direita
do objeto o.
( ) A imagem é virtual, invertida e menor, pois, com
certeza, essa lente delgada é divergente.
( ) O aumento linear transversal da lente vale – 0,5cm, e
a distância do objeto em relação ao centro óptico da
lente vale 12cm.
( ) A intersecção do eixo principal com a reta que une a
extremidade do objeto o à extremidade da imagem i
determina exatamente o ponto antiprincipal, objeto
da lente delgada.
Página 3
16. (Ufpe 2011) A figura mostra uma montagem onde um
objeto foi colocado sobre o eixo ótico distando 4,2 cm de
uma lente convergente de distancia focal f = 4 cm. Calcule o
fator de ampliação, em modulo, para a montagem descrita.
17. (Unifesp 2011) Uma lente convergente pode servir para
formar uma imagem virtual, direita, maior e mais afastada
do que o próprio objeto. Uma lente empregada dessa
maneira é chamada lupa, e é utilizada para observar, com
mais detalhes, pequenos objetos ou superfícies.
Um perito criminal utiliza uma lupa de distância focal igual
a 4,0 cm e fator de ampliação da imagem igual a 3,0 para
analisar vestígios de adulteração de um dos números de
série identificador, de 0,7 cm de altura, tipados em um
motor de um automóvel.
Responda:
a) Qual a distância, ao longo do eixo ab, do centro óptico da
lente à imagem CD?
b) Qual a distância focal da lente?
c) Qual a ampliação linear transversal?
Parte II
TEXTO PARA A PRÓXIMA QUESTÃO:
Dados:
Aceleração da gravidade: g = 10 m/s2
Densidade da água: ρa = 1,0 g/cm3 = 1000 kg/m3
Velocidade da luz no vácuo: c = 3,0 ⋅ 108 m/s
Pressão atmosférica: Patm = 1,0 ⋅ 105 N/m2
1 litro = 1 dm3 = 10−3 m3
a) A que distância do número tipado no motor o perito
deve posicionar a lente para proceder sua análise nas
condições descritas?
b) Em relação à lente, onde se forma a imagem do número
analisado? Qual o tamanho da imagem obtida?
18. (Ufu 2011) Na última copa do mundo, telões instalados
em várias cidades transmitiram, ao vivo, os jogos da seleção
brasileira. Para a transmissão, foram utilizados
instrumentos ópticos chamados de projetores, que são
compostos de uma lente convergente que permite a
formação de imagens reais e maiores que um objeto (slides,
filmes, etc). A figura abaixo mostra, de maneira
esquemática, a posição do objeto e da imagem ao longo do
eixo ab de uma lente esférica delgada, tal como as usadas
em projetores. AB é o objeto, e CD, a imagem de AB
conjugada pela lente.
www.soexatas.com
1 ano - luz = 9,461⋅ 1015 m
Calor específico da água: c a = 1 cal/gºC = 4000 J/KgºC
1 eV = 1,6 ⋅ 1019 J
1 cal = 4,2 J
1. (Ufjf 2011) O olho mágico é um dispositivo óptico de
segurança residencial constituído simplesmente de uma
lente esférica. Quando um visitante está a 1 m da porta,
2
esse dispositivo óptico forma, para o observador, no
interior da residência, uma imagem três vezes menor e
direita do rosto do visitante. É correto afirmar que a
distância focal e o tipo da lente que constituem o olho
mágico são, respectivamente:
a) − 1 m , divergente.
2
1
b) −
m , divergente.
4
c) 1 m , convergente.
4
d) 1 m , convergente.
2
e) − 1 m , convergente.
4
Página 4
No manual da webcam, ele descobriu que seu sensor de
2. (Ufjf 2006) Considere um objeto e uma lente delgada de
vidro no ar. A imagem é virtual e o tamanho da imagem é
duas vezes o tamanho do objeto. Sendo a distância do
objeto à lente de 15 cm:
a) Calcule a distância da imagem à lente.
b) Calcule a distância focal da lente.
c) Determine a distância da imagem à lente, após
mergulhar todo o conjunto em um líquido, mantendo a
distância do objeto à lente inalterada. Neste líquido, a
distância focal da lente muda para aproximadamente 65
cm.
d) Determine a nova ampliação do objeto fornecida pela
lente.
3. (Ufjf 2003) A glicerina é uma substância transparente,
cujo índice de refração é praticamente igual ao do vidro
comum. Uma lente, biconvexa, de vidro é totalmente
imersa num recipiente com glicerina. Qual das figuras a
seguir melhor representa a transmissão de um feixe de luz
através da lente?
imagem tem dimensão total útil de 6 × 6 mm2 , com
500 × 500 pixels. Com estas informações, determine
a) as dimensões do espaço ocupado por cada pixel;
b) a distância L entre a lente e um objeto, para que este
fique focalizado no sensor;
c) o diâmetro máximo D que uma pequena esfera pode ter,
para que esteja integralmente dentro do campo visual
do microscópio, quando focalizada.
Note e adote:
Pixel é a menor componente de uma imagem digital.
Para todos os cálculos, desconsidere a espessura da
lente.
2. (Fuvest 2013) A extremidade de uma fibra ótica adquire
o formato arredondado de uma microlente ao ser aquecida
por um laser, acima da temperatura de fusão. A figura
abaixo ilustra o formato da microlente para tempos de
aquecimento crescentes (t1<t2<t3).
Considere as afirmações:
Parte III
1. (Fuvest 2014) Um estudante construiu um microscópio
ótico digital usando uma webcam, da qual ele removeu a
lente original. Ele preparou um tubo adaptador e fixou uma
lente convergente, de distância focal f = 50 mm, a uma
distância d = 175 mm do sensor de imagem da webcam,
como visto na figura abaixo.
I. O raio de curvatura da microlente aumenta com tempos
crescentes de aquecimento.
II. A distância focal da microlente diminui com tempos
crescentes de aquecimento.
III. Para os tempos de aquecimento apresentados na figura,
a microlente é convergente.
Está correto apenas o que se afirma em
(Note e adote: a luz se propaga no interior da fibra ótica, da
esquerda para a direita, paralelamente ao seu eixo; a fibra
está imersa no ar e o índice de refração do seu material é
1,5.)
a) I.
b) II.
c) III.
d) I e III.
e) II e III.
3. (Unesp 2012) Em um experimento didático de óptica
geométrica, o professor apresenta aos seus alunos o
diagrama da posição da imagem conjugada por uma lente
esférica delgada, determinada por sua coordenada p’, em
função da posição do objeto, determinada por sua
coordenada p, ambas medidas em relação ao centro óptico
da lente.
www.soexatas.com
Página 5
quadradas do solo com, no mínimo, 900 m2 ,
correspondente a um pixel (elemento unitário de imagem)
do sensor óptico da câmara. Qual a distância focal dessa
lente e a área de cada pixel sobre a qual a imagem da
superfície da Terra é conjugada?
6. (Unesp 2009) O Landsat 7 é um satélite de
sensoriamento remoto que orbita a 700 km da superfície da
Terra. Suponha que a menor área da superfície que pode
ser fotografada por esse satélite é de 30 m ⋅ 30 m ,
correspondente a um pixel, elemento unitário da imagem
conjugada no sensor óptico da sua câmara fotográfica. A
lente dessa câmara tem distância focal f = 5,0 cm. Supondo
que os pixels sejam quadrados, qual o comprimento dos
lados de cada quadrado?
Analise as afirmações.
I. A convergência da lente utilizada é 5 di.
II. A lente utilizada produz imagens reais de objetos
colocados entre 0 e 10 cm de seu centro óptico.
III. A imagem conjugada pela lente a um objeto linear
colocado a 50 cm de seu centro óptico será invertida e
1
da altura do objeto.
terá
4
Está correto apenas o contido em
a) II.
b) III.
c) I e II.
d) I e III.
e) II e III.
4. (Unesp 2010) Escolhido como o Ano Internacional da
Astronomia, 2009 marcou os 400 anos do telescópio
desenvolvido pelo físico e astrônomo italiano Galileu
Galilei. Tal instrumento óptico é constituído de duas lentes:
uma convergente (objetiva) e outra divergente (ocular). A
tabela indica o perfil de 4 lentes I, II, III e IV que um aluno
dispõe para montar um telescópio como o de Galileu.
Lente
I
II
III
IV
Perfil
Biconvexa
Planocôncava
Convexocôncava
Planoconvexa
7. (Fuvest 2009) Na montagem de uma exposição, um
decorador propôs a projeção, através de uma lente
pendurada em um suporte fixo, da imagem de duas
bandeirinhas luminosas, B1 e B2, sobre uma tela. Em sua
primeira tentativa, no entanto, apenas a imagem de B1
pôde ser vista na tela (primeira montagem). Para viabilizar,
então, sua proposta, o decorador deslocou a lente para
baixo, obtendo, assim, as imagens das duas bandeirinhas
sobre a tela (segunda montagem).
As bandeirinhas encontram-se reproduzidas na folha de
respostas, assim como, em linhas tracejadas, a posição da
lente e a imagem obtida na primeira montagem. Para
visualizar as imagens que passam a ser observadas na
segunda montagem, utilizando o esquema a seguir:
Para que o telescópio montado pelo aluno represente
adequadamente um telescópio semelhante ao
desenvolvido por Galileu, ele deve utilizar a lente.
a) I como objetiva e a lente II como ocular.
b) II como objetiva e a lente I como ocular.
c) I como objetiva e a lente IV como ocular.
d) III como objetiva e a lente I como ocular.
e) III como objetiva e a lente IV como ocular
5. (Unesp 2009) Desde maio de 2008 o IBAMA recebe
imagens do ALOS, um satélite japonês de sensoriamento
remoto que orbita a cerca de 700 km da superfície da Terra.
Suponha que o sistema óptico desse satélite conjugue
imagens nítidas no seu sensor quando este se localiza 4,0
cm atrás da lente (objetiva) e seja capaz de fotografar áreas
www.soexatas.com
a) Determine, a partir da imagem correspondente à
primeira montagem (em linha tracejada), a posição do foco
da lente, identificando-a na figura pela letra F.
b) Construa a imagem completa que a bandeirinha B2
projeta sobre a tela, na segunda montagem, traçando as
linhas de construção necessárias e indicando as imagens de
Página 6
C e D, por C' e D', respectivamente.
c) Construa a imagem completa que a bandeirinha B1
projeta sobre a tela, na segunda montagem, traçando as
linhas de construção necessárias e indicando as imagens de
A e B, por A' e B', respectivamente.
8. (Unifesp 2009) Dentro de um aquário sem água são
colocados uma lente delgada convergente e um parafuso,
posicionado frontalmente à lente, ambos presos a suportes,
conforme a figura.
Nessas condições, a imagem conjugada pela lente é direita
e tem o dobro do tamanho do objeto.
a) Calcule a razão f/p, entre a distância focal da lente e a
distância do objeto ao centro óptico da lente.
b) Preenchido totalmente o aquário com água, a distância
focal da lente aumenta para 2,5 vezes a distância focal na
situação anterior, e a lente mantém o comportamento
óptico convergente. Para as mesmas posições da lente e do
objeto, calcule o aumento linear transversal para a nova
imagem conjugada pela lente.
9. (Unesp 2009) É possível improvisar uma objetiva para a
construção de um microscópio simples pingando uma gota
de glicerina dentro de um furo circular de 5,0 mm de
diâmetro, feito com um furador de papel em um pedaço de
folha de plástico. Se apoiada sobre uma lâmina de vidro, a
gota adquire a forma de uma semiesfera. Dada a equação
dos fabricantes de lentes para lentes imersas no ar,
C=
 1
1
1 
= ( n − 1) ⋅ 
+
 , e sabendo que o índice de
f
 R1 R 2 
refração da glicerina é 1,5, a lente plano-convexa obtida
com a gota terá vergência C, em unidades do SI, de:
a) 200 di.
b) 80 di.
c) 50 di.
d) 20 di.
e) 10 di.
www.soexatas.com
Página 7