Discordâncias, m - PMT-USP

PMT-2200 – Ciência dos Materiais
DISCORDÂNCIAS
Prof. Dr. André Paulo Tschiptschin
Cálculo da resistência teórica de um cristal
A resistência teórica de um cristal é determinada pela
natureza das suas forças interatômicas.
Os cálculos dessa resistência podem ser feitos para o
cristal submetido a dois estados de tensão
diferentes:
tensão normal uniaxial
a)
tensão normal uniaxial
b)
tensão de cisalhamento
Os dois tipos de estados de tensões levam a dois tipos
diferentes de falhas:
tensão de cisalhamento
a)
Cisalhamento
b)
Clivagem
Cálculo da resistência teórica de um cristal
A resistência teórica de um cristal é determinada pela natureza das forças
interatômicas e pode ser calculada, segundo modelo proposto por Orowan,
supondo que duas superfícies novas (com energias de superfície associadas)
devem ser criadas no interior do cristal.
Ao se tentar separar um átomo de sua posição de equilíbrio a0 é necessário
superar uma barreira de energia potencial e exercer uma força σmax :
σ max ≅
E
π
sendo E o módulo de Young
Cálculo da resistência teórica de um cristal
Cálculo da tensão necessária para escorregar um
plano cristalino perfeito sobre outro
Cálculo da tensão necessária para escorregar um plano cristalino perfeito sobre outro
Cálculo da tensão necessária para escorregar um
plano cristalino perfeito sobre outro
Esquema ilustrativo da posição dos átomos, usado para avaliar a tensão crítica
de cisalhamento para o escorregamento de planos.
⇒ τ max
G
≅
5,1
Tensão de cisalhamento máxima teórica é de 3 a 8 ordens de grandeza maior que a
observada experimentalmente
Cálculo da resistência ao cisalhamento teórica de um cristal
Cálculo da tensão necessária para escorregar um plano
cristalino sobre outro na presença de uma discordância
Discordância em cunha
Esquema ilustrativo do rearranjo atômico
nas vizinhanças de uma discordância em
cunha, sob a ação de uma tensão.
Cálculo da tensão necessária para escorregar um plano
cristalino sobre outro na presença de uma discordância
A tensão calculada levando em
conta a alteração da energia dos
átomos em função da existência de
um defeito é da ordem da
observada experimentalmente.
A existência de discordâncias foi
postulada nos anos 30 por Taylor,
baseado nestes cálculos.
Variação da energia de reticulado com a posição de uma discordância
Comparação entre a tensão teórica e a tensão real
As tensões teóricas de cisalhamento e de ruptura calculadas anteriormente
são da ordem de GPa.
As tensões de ruptura (separação de planos atômicos) observadas em
ensaios de materiais frágeis (p.e os materiais cerâmicos) , nos quais logo
após o regime elástico, ocorre ruptura, são ordens de grandeza menores
que a calculada.
Os materias reais podem ter pequenas trincas internas em cujas
extremidades ocorre forte concentração de tensões. As tensões
teóricas podem ser atingidas nas pontas destas trincas. A teoria de
Griffith explica o fato.
As tensões de escoamento (escorregamento de planos atômicos)
observadas em ensaios de materiais dúteis (p.e grande parte dos materiais
metálicos), nos quais logo após o regime elástico ocorre extensa deformação
plástica, são ordens de grandeza menores.
Antes de a tensão teórica teórica de cisalhamento ser atingida começa a ocorrer
movimentação e multiplicação de discordâncias, sob tensões aplicadas
muito menores. Estas discordâncias são responsáveis pela deformação
plástica do material.
Discordâncias em cunha e em hélice
Geometria de discordâncias simples.
(a) discordância em cunha
(b) discordância em hélice
Circuito de Burgers e vetor de Burgers
Vetor de Burgers e circuito de Burgers:
(a) discordância em cunha Î o vetor de Burgers é perpendicular à linha
(b) discordância em hélice Î o vetor de Burgers é paralelo à linha
Discordâncias mistas
Anel de discordância visto em corte mostrando regiões de:
(a) discordância em cunha Î vetor de Burgers perpendicular à linha
(b) discordância em hélice Î vetor de Burgers paralelo à linha
Movimentação de discordâncias
Para que uma
discordância se
movimente é necessário
que a linha e o vetor de
Burgers estejam
contidos no plano de
escorregamento.
A discordância em
cunha anda na direção
de aplicação das
tensões.
A discordância em
hélice anda
perpendicularmente à
direção de aplicação das
tensões
Criação de um degrau de escorregamento pela movimentação de: a) uma discordância em
cunha; b) uma discordância em hélice no plano de escorregamento
Movimento relativo de discordâncias
Sob a ação da tensão de cisalhamento τ, discordâncias de sinais opostos se
movimentam em direções opostas, produzindo escorregamento no mesmo sentido
Energia de uma discordância
Deformação por cisalhamento associada à
discordância em hélice
Energia elástica associada à presença de uma
discordância em hélice no reticulado
Energia elástica associada à presença de uma
discordância em cunha no reticulado
Modelo geométrico para cálculo da deformação ao redor de uma discordância em hélice
Geometria dos campos de tensão e deformação em
torno de discordâncias
Campos de tensão e de deformação ao redor de (a) uma discordância em cunha e (b) uma
discordância em hélice.
Tensão de linha
Modelo para o cálculo da tensão de linha de uma discordância, quando
uma discordância encontra obstáculos B e C e começa a encurvar sob a
ação da tensão.
Ascensão e escorregamento com desvio de discordâncias
Escorregamento com desvio de discordância em hélice (o vetor de Burgers e a discordância
devem pertencer simultaneamente a diversos planos de escorregamento)
Ascenção de discordâncias em cunha (depende de difusão – processo é ativado
termicamente)
Escorregamento com desvio de discordâncias
Interação entre campos de tensão
de discordâncias
repulsão
atração
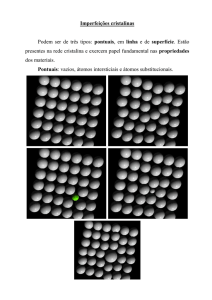
Reticulado
perfeito
Lacuna
Intersticial
Intersticiais
Contorno de grão de pequeno ângulo
produzido pelo alinhamento de discordâncias
em cunha de mesmo sinal
Interação entre discordâncias
Atração e repulsão entre discordâncias
Formação de degraus em discordâncias
Exemplo de intereseção de duas discordância em cunha criando uma discordância em
degrau
Formação de degraus em discordâncias
Exemplo de intereseção de duas discordância em cunha criando dois planos de
escorregamento em degrau
Interação entre discordâncias
Formação de degraus com acúmulo de lacunas
Movimentação de uma discordância em hélice deixando atrás de si uma fileira de lacunas
Reações entre discordâncias
Reação entre duas discordâncias parciais formando uma unitária de acordo com a reação:
−
a
a
a
[211] + [211] → [110]
6
6
2
Reações entre discordâncias formando discordâncias bloqueadas
Reação entre duas discordâncias formando uma terceira discordância bloqueada
O vetor de Burgers não se encontra nos planos de escorregamento [111].
Multiplicação de discordâncias (Fonte de Frank-Read)
Cada segmento da
dsicordância anda em
direções e sentidos
diferentes, determinados
pela orientação do vetor
de Burgers e da linha.
Movimento de uma discordância bloqueada em suas extremidades D e D’, gerando
múltiplas discordâncias. Note que os segmentos m e n no anel se anulam por serem de
sinais contrários.
Multiplicação de discordâncias (Fonte de Frank-Read)
Fonte de Frank Read em um cristal de Si
Multiplicação de discordâncias (Fonte de Frank-Read)
Reações entre discordâncias (Anéis de discordâncias)
Formação de anéis de discordãncias em torno de precpitados.
Anéis de Orowan
Formação de florestas
Observação de discordâncias
Fotografias de discordâncias (a) vistas de topo por meio de figuras de corrosão
em LiF 290X (b) em cristal Na Cl envenenadas com prata 290 X (c) em
monocristal de Nb, microscopia eletrônica de transmissão 11600X.
Deformação plástica
Escorregamento
macroscópico em
um monocristal
Escorregamento em
um monocristal de
zinco
Linhas de escorregamento em liga
Cu-2% Al policristalina. 850X.
Deformação plástica
Esquema ilustrativo de linhas e bandas de escorregamento
Sistemas de escorregamento
Um sistema de escorregamento é
formado por um plano e uma direção
de escorregamento.
O escorregamento nos cristais ocorre
preferencialmente em planos e
direções compactas.
A Tabela ao lado mostra o número
de sistemas de escorregamento
existentes nos diversos reticulados
cristalinos
Tensão de cisalhamento projetada
O escorreagmento ocorre no
plano e na direção de
escorregamento.
Para calcular a tensão
efetiva para escorregamento
devemos projetar a força no
plano e na direção
Esquema geométrico para cálculo da tensão de cisalhamento projetada
Tensão crítica de tração não projetada
O escorregamento em um
determinado sistema ocorre assim
que a tensão crítica projetada atinja
um valor crítico para movimentação
de discordâncias naquele sistema.
A tensão crítica de cisalhamento é
atingida em um dos sistemas de
escorregamento existentes,
iniciando o processo de
deformação.
Com o aumento da tensão outros
sistemas de escorregamento
entram em ação.
Variação da tensão crítica não projetada com os ângulos φ e λ
Encruamento e recuperação em monocristais CFC
Estágio 1 - Monocristais CFC possuem 12
sistemas de escorregamento. A deformação
inicia com ativação de um único sistema de
escorregamento. É um estágio de
escorregamento fácil e baixa taxa de
encruamento.
Estágio 2 - Para ~10% de deformação outros
sistemas de escorregamento começam a
operar levando ao cruzamento de
discordâncias e formação de emaranhados.
O encruamento cresce linearmente com a
deformação.
0
0,1
0,2
0,3
0,4
Três estágios de deformação em
monocristal CFC
Estágio 3 - Para ~ 40% de deformação
começa a ocorrer rearranjo de discordâncias,
com aniquiliação, escorregamento com
desvio, ascenção, etc. diminuindo a taxa de
encruamento devido à recuperação
Encruamento e recuperação em monocristais
O Fe CCC com 48 sistemas de
escorregamento entra direto no estágio
3 de deformação, pois múltiplos
sistemas de escorregamento operam
simultânemanete desde o início da
deformação.
O Cu CFC com 12 sistemas de
escorregamento apresenta os três
estágios de deformação, conforme
discutido anteriormente.
Curvas tensão deformação em cisalhamento de
monocristais de Mg, Cu e Fe
O Mg com estrutura HC possui
somente três sistemas de
escorregamento, todos no plano basal.
As discordâncias se movimentam
sempre no mesmo plano e
praticamente não sofrem cruzamento.
Toda a deformação ocorre no estágio 1
de escorregamento fácil.
Encruamento em monocristais
Microestrutura típica de Al CFC
deformado na temperatura
ambiente (a) 2% e (b) 20%
Microestrutura típica de ferro
CCC deformado na temperatura
ambiente (a) 9% e (b) 20%
Encruamento e recuperação em monocristais CFC
Escorregamento com desvio em monocristal de Cu. 5000X.
Encruamento e recuperação em monocristais CFC
Formação de um contorno de pequeno ângulo por rearranjo de
discordâncias, por ascenção e escorregamento, em um cristal
deformado em flexão.
Deformação de policristais
Quando metais policristalinos são deformados, a
deformação plástica em cada grão ocorre em
um sistema de escorregamento distinto,
gerando incompatibilidae de deformação entre
os grãos.
Para que haja compatibilidade de deformação
entre grãos vizinhos é necessário que haja 5
sistemas de escorregamento independentes em
cada grão, condição de Von Mises.
Os metais CFC e CCC que possuem
respectivamente 12 e 48 sistemas de
escorregamento preenchem essa condição.
Os metais hexagonais (p.e Mg), com apenas
três sistemas de escorregamento apresentam
baixa dutilidade por não preencherem a
condição de Von Mises
Deformação de policristais
Curvas tensão-deformação para policristais (a) dútil e (b) frágil .
Curvas tensão-deformação para monocristais CFC .
A necessidade de
operação de 5 sistemas
de escorregamento
independentes em cada
grão, desde o início da
deformação, faz com
que a curva tensão
deformação de
policristais apresente
aspecto semelhante à
do estágio 3 da curva
de monocristais CFC,
devido à forte interação
e cruzamento de
discordâncias,
escorregamento com
desvio, rearranjo e
aniquiliação, etc.