O Capacitor

Capacitância
Objetivos:
●
●
●
A natureza dos capacitores e como determinar a
quantidade que mede sua habilidade de
armazenar carga?
Com os capacitores de comportam em circuitos?
Como determinar a quantidade de energia
armazenada em um capacitor?
Sobre a Apresentação
Todas as gravuras, senão a maioria, são dos livros:
●
●
●
Sears & Zemansky, University Physics with Modern Physics – ed.
Pearson, 13a edition
Wolfgang Bauer and Gary D. Westfall, University Physics with
Modern Physics – ed. Mc Graw Hill, Michigan State University, 1a
edition
Halliday & Resnick, Fundamentals of Physics, 9a edition.
O Capacitor
“Um capacitor é um dispositivo que armazena energia potencial elétrica e
carga elétrica.” (Sears)
Mecanicamente: Um capacitor consiste de dois corpos metálicos
eletricamente isolados.
+ +
+
+
+
-
-
-
-
-
-
-
-
V
+
+
+
-
O trabalho realizado para mover as cargas é
armazenado na forma de Energia Potencial
Elétrica.
+
Para armazenar energia este dispositivo deve
ser conectado a uma fonte (como uma bateria)
para bombear as cargas elétricas de um metal
para o outro.
Tipos de Capacitores
Eletrolíticos, cerâmicos, tântalo, polipropileno, mica, poliestireno, …,
“Super Capacitores”
Super Capacitores
http://br.mouser.com/Passive-Components/Capacitors/Supercapacitors-Ultracapacitors/_/N-5x76s
Aplicações
Capacitor de
Placas Paralelas
Considere um capacitor constituído de duas placas de área A, paralelas e
separadas por uma distância d.
Para os cálculos a seguir, efeitos de borda do campo elétrico na placa serão
ignorados.
Capacitor de
Placas Paralelas
Primeiro determine o campo elétrico no interior das placas usando uma
superfície Gaussiana que contenha toda a carga da placa superior, como
ilustrado abaixo.
Em seguida, determine a diferença de potencial elétrico entre as duas placas
pela integral do campo elétrico pelo caminho da seta azul,
Tomando o potencial na placa negativo omo nulo, e na positiva como V:
Capacitor de
Placas Paralelas
Eliminando o campo elétrico na expressão da carga encontramos que este
se relaciona com o potencial pela expressão:
A constante à frente da variação de potencial depende apenas de
características do capacitor como área das placas e distância entre elas.
Esta constante é chamada de Capacitância:
A equação da carga fica:
Unidade para Capacitância:
Capacitor de
Placas Cilíndricas
A figura ao lado representa uma vista superior de um capacitor de placas
cilíndricas de altura h, raios interno e externo, a e b, e carregado de uma
carga q. De forma semelhante ao feito anteriormente, o campo entre as
placas deve ser determinada pela Lei de Gauss, sobre a superfície Gaussiana
(cilindro em vermelho),
Como o campo é variável com o raio, este deve ser
empregado no cálculo da diferença de potencial entre
as cargas é calculado pela integral de linha, pelo
caminho verde,
Capacitor de
Placas Cilíndricas
Portanto, tomando o potencial na placa negativa como zero, para um
capacitor de placas cilíndricas,
ou seja,
com
Como no capacitor de placas paralelas, a capacitância depende das
características geométricas das placas, tais como os raios e da altura do
capacitor.
Capacitor de
Placas Esféricas
A figura a baixo representa um corte de um capacitor de placas esféricas
concêntricas, de raios ra e rb. A carga nas placas são ±Q. Novamente o
campo é variável com o raio r, e seu valor pode ser encontrado pela Lei de
Gauss sobre a superfície Gaussiana (esfera em roxo) de raio r:
A diferença de potencial entre as cargas é calculado
pela integral de linha, pelo caminho verde,
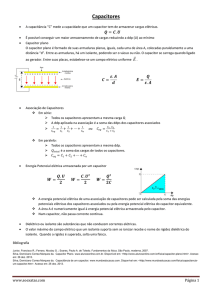
Associação de
Capacitores
Paralelo: No circuito abaixo, três capacitores são associados em paralelo.
Para determinar a capacitância equivalente, observe que todos os
capacitores estão sobre o mesmo potencial elétrico, e portanto suas cargas
serão:
e a carga total armazenada nos capacitores,
Para n capacitores em paralelo,
Associação de
Capacitores
Série: No circuito abaixo, três capacitores são associados em série. Neste
caso, o que se tem em comum nos capacitores é a carga elétrica. Devido a
sua distribuição em série, todos os capacitores serão carregados com a
mesma carga, porem potenciais diferentes:
A soma dos potenciais nos capacitores
deve ser igual ao potencial da fonte,
Para n capacitores em série,
Exemplo
No circuito abaixo os capacitores C1 = C6 = 3,0µF; C3 = C5 = 2 C2 = 2 C4
= 4,0µF. Determine a capacitância equivalente e as tensões em cada
capacitor.
O problema consiste em encontrar
padrões de associação em série e
paralelo no circuito.
Antes de começar a resolver o problema
uma breve dissertação sobre dispositivos
em série e paralelo.
Série/Paralelo
Série: Dispositivos em série, significa que por eles deve passar a mesma
corrente, como ilustra nos 3 circuitos abaixo:
Observe que nos circuitos exemplos acima, não existem nós (junção de três
ou mais fios) entre os dispositivos, de forma que a corrente possui apenas um
caminho para seguir, que é através dos dispositivos em série.
Paralelo: Já os dispositivos em paralelo possuem o mesmo potencial
elétrico sobre eles, o que significa que compartilham os mesmos nós:
Como estudamos no capítulo passado, o potencial em um condutor é
constante, e portanto em qualquer ponto do fio metálico o potencial é sempre
o mesmo.