Lista de Física – 3° Bimestre - Colégio dos Santos Anjos – Unidade

Lista de Física – 3° Bimestre
1. Um automóvel de massa 1,2x103 kg se desloca com velocidade de 12,0m/s. Quando
avista um obstáculo, aciona o freio até parar. Qual o trabalho realizado pelos freios do
carro?
2. Newton, brincando com seu filho Einstein constrói um pequeno canhão para lançar
bolas. Para isso, ele utiliza um tubo de plástico com 40 cm de comprimento, uma mola
com comprimento de 20 cm e uma bola de tênis com massa igual a 235g. A bola de
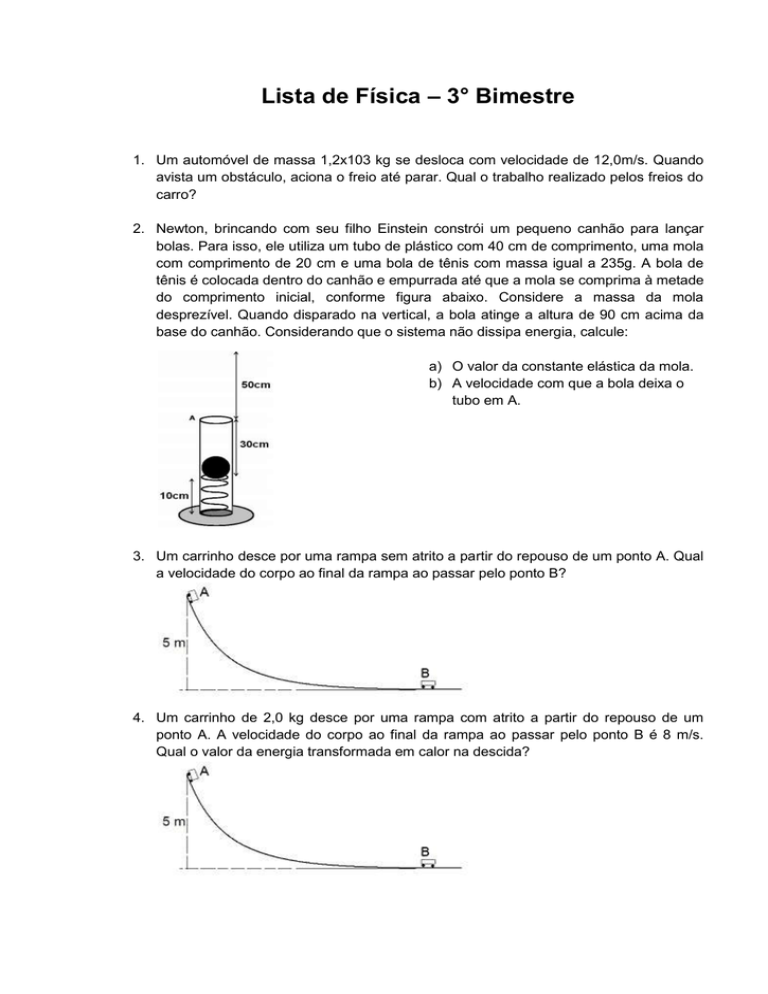
tênis é colocada dentro do canhão e empurrada até que a mola se comprima à metade
do comprimento inicial, conforme figura abaixo. Considere a massa da mola
desprezível. Quando disparado na vertical, a bola atinge a altura de 90 cm acima da
base do canhão. Considerando que o sistema não dissipa energia, calcule:
a) O valor da constante elástica da mola.
b) A velocidade com que a bola deixa o
tubo em A.
3. Um carrinho desce por uma rampa sem atrito a partir do repouso de um ponto A. Qual
a velocidade do corpo ao final da rampa ao passar pelo ponto B?
4. Um carrinho de 2,0 kg desce por uma rampa com atrito a partir do repouso de um
ponto A. A velocidade do corpo ao final da rampa ao passar pelo ponto B é 8 m/s.
Qual o valor da energia transformada em calor na descida?
5. Uma das modalidades presentes nas olimpíadas é o salto com vara. As etapas de um
dos saltos de um atleta são representadas na figura:
Desprezando-se as forças dissipativas (resistência do ar e atrito), para que o salto
atinja a maior altura possível, ou seja, o máximo de energia seja conservado, é
necessário que:
a) a energia cinética, representada na etapa I, seja totalmente convertida em energia
potencial elástica representada na etapa IV.
b) a energia cinética, representada na etapa II, seja totalmente convertida em energia
potencial gravitacional, representada na etapa IV.
c) a energia cinética, representada na etapa I, seja totalmente convertida em energia
potencial gravitacional, representada na etapa III.
d) a energia potencial gravitacional, representada na etapa II, seja totalmente
convertida em energia potencial elástica, representada na etapa IV.
e) a energia potencial gravitacional, representada na etapa I, seja totalmente
convertida em energia potencial elástica, representada na etapa III.
6. Um brinquedo que muito agrada às crianças são os lançadores de objetos em uma
pista. Considere que a mola da figura a seguir possui uma constante elástica k = 8 000
N/m e massa desprezível. Inicialmente, a mola está comprimida de 2,0 cm e, ao ser
liberada, empurra um carrinho de massa igual a 0,20 kg. O carrinho abandona a mola
quando esta atinge o seu comprimento relaxado, e percorre uma pista que termina em
uma rampa. Considere que não há perda de energia mecânica por atrito no
movimento do carrinho. Qual a velocidade do carrinho quando ele abandona a mola e
qual a altura da rampa no instante em que o carrinho tem velocidade de 2,0 m/s,
valem, respectivamente: (considere g = 10m/s²).
7. Para entender os movimentos dos corpos, Galileu discutiu o movimento de uma esfera
de metal em dois planos inclinados sem atritos e com a possibilidade de se alterarem
os ângulos de inclinação, conforme mostra a figura. Na descrição do experimento,
quando a esfera de metal é abandonada para descer um plano inclinado de
determinado nível, ela sempre atinge, no plano ascendente, no máximo, um nível igual
àquele em que foi abandonada.
Se o ângulo de inclinação do plano de subida for reduzido a zero, a esfera
a) manterá sua velocidade constante, pois o impulso resultante sobre ela será nulo.
b) manterá sua velocidade constante, pois o impulso da descida continuará a empurrála.
c) diminuirá gradativamente a sua velocidade, pois não haverá mais impulso para
empurrá-la.
d) diminuirá gradativamente a sua velocidade, pois o impulso resultante será contrário
ao seu movimento.
e) aumentará gradativamente sua velocidade, pois não haverá nenhum impulso
contrário ao seu movimento.
8. Em relação à conservação do momento linear (quantidade de movimento), é
CORRETO afirmar:
a) A conservação de momento linear é aplicada a sistemas isolados em que não há
qualquer interação entre corpos.
b) O momento linear é uma grandeza escalar, onde apenas o módulo do produto da
massa pela velocidade descreve a quantidade de movimento de um corpo.
c) O momento linear é definido pelo produto da massa pela velocidade de um corpo, e
é uma grandeza vetorial, em que a direção e sentido são os mesmos da massa.
d) O momento linear é definido como o produto do módulo da massa pelo módulo da
velocidade, sendo uma grandeza vetorial e possui o mesmo sentido e direção da
velocidade.
e) O momento linear só se aplica a corpos lineares.
9. Um projétil, de massa m = 20 g, é atirado horizontalmente contra um bloco de madeira
de massa M = 9980 g, que está em repouso sobre uma superfície horizontal. O projétil
fica alojado no bloco e o sistema bloco + projétil inicia um movimento com velocidade
v = 0,50 m/s. De acordo com esses dados, é INCORRETO afirmar que:
a) na colisão, ocorre conservação da quantidade de movimento (momento linear).
b) a velocidade inicial do projétil era de 250 m/s .
c) na colisão, ocorre conservação da energia mecânica do sistema.
d) a energia cinética do sistema, imediatamente após a colisão, é de 1,25 J.
e) a quantidade de movimento do projétil, imediatamente antes da colisão, era de 5,0
kg x m/s.
10. O gráfico seguinte representa a projeção da força resultante que atua sobre um corpo,
de massa m, na direção do deslocamento, em função da posição do corpo. O corpo se
desloca da posição D = 0 m até a posição D = 3 m. A variação da energia cinética do
corpo nesse intervalo é:
a) 90 J
b) 20 J
c) 40 J
d) 60 J
e) 30 J
11. Uma partícula se move com velocidade uniforme V ao longo de uma reta e choca-se
frontalmente com outra partícula idêntica, inicialmente em repouso. Considerando o
choque elástico e desprezando atritos, podemos afirmar que, após o choque:
a) as duas partículas movem-se no mesmo sentido com velocidade V/2.
b) as duas partículas movem-se em sentidos opostos com velocidades – V e + V.
c) a partícula incidente reverte o sentido do seu movimento, permanecendo a outra em
repouso.
d) a partícula incidente fica em repouso e a outra se move com velocidade v.
e) as duas partículas movem-se em sentidos opostos com velocidades – V e 2V.
12. Em uma colisão com o chão, após uma queda livre vertical, uma esfera dissipa 36%
de sua energia mecânica. Supondo que a esfera partiu do repouso de uma altura H =
1,0 m e desprezando a resistência do ar, calcule:
a) a altura máxima h atingida após a colisão.
b) o coeficiente de restituição na colisão.
13. (FUVEST) Um vagão A, de massa 10 t, move-se com velocidade escalar igual a 0,40
m/s sobre trilhos horizontal sem atrito até colidir com um outro vagão B, de massa 20
t, inicialmente em repouso. Após a colisão, o vagão A fica parado. A energia cinética
final do vagão B vale:
a) 100J
b) 200J
c) 400J
d) 800J
e)1600J
14. Considere o estudo de uma colisão entre duas partículas A e B que constituem um
Sistema isolado. Verifique quais as proposições corretas e dê como resposta a soma
dos números a elas associados.
(01) Se a colisão entre A e B for elástica, a energia cinética total das partículas
permanece constante durante a colisão.
(02) Se a colisão entre A e B for elástica, a energia mecânica do sistema (soma das
energias cinética e elástica) permanece constante durante a colisão.
(04) Se a colisão entre A e B for elástica, a quantidade de movimento de cada uma
das partículas permanecerá constante.
(08) Se a colisão entre A e B for perfeitamente inelástica, não haverá conservação da
quantidade de movimento do sistema.
(16) Se a colisão entre A e B não for elástica, haverá dissipação de energia mecânica,
porém, haverá conservação da quantidade de movimento total do sistema.
a) 16
b) 18
c) 26
d) 32
e)48
15. Um bloco de madeira de 6,0kg, dotado de pequenas rodas com massa desprezível,
repousa sobre trilhos retilíneos. Quando uma bala de 12g disparada horizontalmente e
na mesma direção dos trilhos se aloja no bloco, o conjunto (bloco + bala) desloca-se
0,70m em 0,50s, com velocidade praticamente constante. A partir destes dados, podese concluir que a velocidade escalar da bala é, em m/s, aproximadamente igual a:
a) 5,0 x 10²
b) 6,0 x 10²
c) 7,0 x 10²
d) 8,0 x 10²
e) 9,0 x 10²
16. Determine o coeficiente de restituição dos seguintes choques:
17. Um carro de 800 kg, parado num sinal vermelho, é abalroado por trás por outro carro,
de 1200 kg, com velocidade de 72 km/h. Imediatamente após o choque, os dois carros
se movem juntos.
a) calcule a velocidade do conjunto logo após a colisão;
b) Prove que o choque não é elástico.
18. Uma bola é solta de uma altura H = 100 m. Ela choca-se com o solo, e atinge na volta,
uma altura máxima de 64 m. Sabendo que a aceleração da gravidade é g = 10 m/s²,
calcular o coeficiente de restituição.
19. Uma bola de borracha de 0,2 kg cai, a partir do repouso, de uma altura H = 1,6 m e,
após o choque frontal com o solo, retorna até uma altura máxima h = 0,4 m. Adotando
g = 10 m/s² e desprezando a resistência do ar, determine:
a) a perda de energia mecânica da bola nesse choque;
b) o coeficiente de restituição no choque.
20. Uma partícula de massa m1=25,0 g e com velocidade inicial v1=100m/s colide,
frontalmente, com outra partícula de massa m2=200g, inicialmente em repouso.
Durante o processo de colisão, o gráfico da força de interação entre as duas partículas
é mostrado na figura ao lado. Com base nessas informações, calcule:
a) O impulso sofrido por cada partícula;
b) A velocidade final de cada partícula imediatamente após a colisão.