2º Caso: a 3 + b 4 = c 5

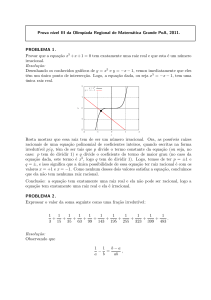
Por meio da equação a x (a x  b y ) m  b y (a x  b y ) m  (a x  b y ) m1 (1)
soluções em inteiros para a equação de Beal: ax + by = cz.
é possível encontrar
Se escolhermos valores para a e b tal que a ≤ b ou a ≥ b, e substituirmos na (1), obtém-se
infinitas soluções em inteiros positivos com fator primo comum a a, b e c.
Na (1), ax + by é o fator primo comum à a, b e c, haja vista que ax + by divide (ax + by)m.
Segundo EULER, “se temos um problema e se não for possível resolvê-lo imediatamente, é prudente
estimar sua dificuldade analisando alguns casos particulares. É o que veremos a seguir.
Dois Casos Particulares para a Veracidade da Conjectura de Beal
1º Caso: se x = y e mdc(x, y, z) = 1
Exemplos:
a3 + b3 = c4, 5, 7, 8, 10, 11, ...
a4 + b4 = c3, 5, 7, 9, 11, 13, ...
a5 + b5 = c2, 3, 4, 6, 7, 8, ...
2º Caso: se x ≠ y e mdc(x.y, z) = 1
Exemplos:
a3 + b4 = c5, 7, 11, 13,17, 19... ou a12 + b12 = c5, 7, 11, 13,17, 19... ou (a4)3 + (b3)4 = c5, 7, 11, 13,17, 19...
a3 + b5 = c4, 7, 8, 10, 11, 13, ... ou a15 + b15 = c4, 7, 8, 10, 11, 13, ... ou (a5)3 + (b3)5 = c4, 7, 8, 10, 11, 13, ...
a3 + b6 = c5, 7, 8, 10, 11, 12, ... ou a18 + b18 = c5, 7, 8, 10, 11, 12, ... ou (a6)3 + (b3)6 = c5, 7, 8, 10, 11, 12, ...
MÉTODO DE RESOLUÇÃO DA EQUAÇÃO DE BEAL PARA OS DOIS CASOS
1º Caso: a3 + b3 = c4
Como o expoente de a e b é 3, logo, substituindo na (1) x e y por 3, obtém-se:
a 3 (a 3  b 3 ) m  b 3 (a 3  b 3 ) m  (a 3  b 3 ) m1
(2)
Como na equação, a3 + b3 = c4, o membro da esquerda tem expoente 3 e o da direita, expoente 4,
logo, temos que encontrar dois números m e m + 1 que seja possível decompor m em potência
de 3 e m + 1 em potência de 4. Isso só será possível se m e m + 1 forem, respectivamente,
múltiplo de 3 e 4. Logo, m = 12k – 9 e m + 1 = 12k – 8.
Substituindo os valores de m e m + 1 na (2), vem:
a 3 (a 3  b 3 )12k 9  b 3 (a 3  b 3 )12k 9  (a 3  b 3 )12k 8
Seja k = a = b = 1. Substituindo os valores de k, a e b na (3), vem:
(3)
13 (13  13 ) 3  13 (13  13 ) 3  (13  13 ) 4
23 + 23 = 24 ou 8 + 8 = 16
Solução: a = b = c = 2 (Fator primo comum: 2)
Se escolhermos, por exemplo, k = a = 1 e b = 2, e substituirmos na (3), obtém-se:
13 (13  2 3 ) 3  2 3 (13  2 3 ) 3  (13  2 3 ) 4
93 + 23(93) = 94 ou 93 + 183 = 94
Solução: a = c = 9 e b = 18 (Fator primo comum: 3)
Conclusão. Qualquer que seja o valor de k ≠ 0, a, b e c vão ter sempre um fator primo comum à
a, b e c
2º Caso: a3 + b4 = c5
Encontrar solução em inteiros para a equação a3 + b4 = c5, é o mesmo que encontrar solução em
inteiros para a equação a12 + b12 = c5, haja vista que podemos escrever a12 + b12 = c5 como:
(a4)3 + (b3)4 = c5. Como o expoente de a e b é 12, logo, substituindo na (3) x, y e z por 12, obtémse:
a12 (a12  b12 ) m  b12 (a12  b12 ) m  (a12  b12 ) m1
(4)
Como na equação, a12 + b12 = c5, o membro da esquerda tem expoente 12 e o da direita,
expoente 5, logo, temos que encontrar dois números m e m + 1 que seja possível decompor m
em potência de 12 e m + 1 em potência de 5. Isso só será possível se m e m + 1 forem,
respectivamente, múltiplo de 12 e 5. Logo, m = 60k –36 e m + 1 = 60k – 35.
Substituindo os valores de m e m + 1 na (4), vem:
a12 (a12  b12 ) 60k 36  b 3 (a 3  b 3 ) 60k 36  (12 3  12 3 ) 60k 35
(5)
Seja k = a = b = 1. Substituindo os valores de k, a e b na (8), vem:
2 24  2 24  2 25 ou (28 ) 3  (2 6 ) 4  (2 5 ) 5 ou 2563 + 644 = 325
Solução: a = 256, b = 64 e c = 32 (Fator primo comum: 2)
Se escolhermos, por exemplo, k = a = 1 e b = 2, e substituirmos na (5), obtém-se:
(40978 ) 3  (2(4097 6 )) 4  (4097 5 ) 5
Solução: a = 40978, b = 2(4097)6 e c = 40975 (Fator primo comum: 241)
OUTROS DOIS CASOS PARTICULARES PARA OS QUAIS A CONJECTURA DE
BEAL É VERDADEIRA
1º Caso: se a = b = c = 2, x = y = 2n > 2 e z = 2n + 1 > 2, então, a equação de Beal tem solução.
Demonstração:
22n + 22n = 22n+1
22n (1 + 1) = 22n+1
.
2 = 22n+1 2–2n
2 = 22n+1 + ( – 2n)
2=2
Exemplos
24 + 24 = 25 (o 2 é um fator primo comum a “a, b e c”)
26 + 26 = 27 (o 2 é um fator primo comum a “a, b e c”)
28 + 28 = 29 (o 2 é um fator primo comum a “a, b e c”)
E assim por diante.
2º Caso: se a = b = c = 2, x = y = 2n + 1 > 2 e z = 2n + 2 > 2, então, a equação de Beal tem
solução.
Demonstração:
22n+1 + 22n+1 = 22n+2
22n+1 (1 + 1) = 22n+2
.
2 = 22n+2 2–(2n+1)
2 = 22n+2 + ( – 2n – 1)
2=2
Exemplos
23 + 23 = 24 (o 2 é um fator primo comum a “a, b e c”)
25 + 25 = 26 (o 2 é um fator primo comum a “a, b e c)”
27 + 27 = 28 (o 2 é um fator primo comum a “a, b e c”)
E assim por diante.
QUATRO CASOS PARTICULARES PARA OS QUAIS A EQUAÇÃO DE BEAL
NÃO TEM SOLUÇÃO
Se x, y, z > 2 e mdc(x, y, z) >1, então, a equação de Beal não tem solução. Se não, vejamos:
1º Caso: x = y = 2n +1 e z múltiplo de 2n + 1.
Exemplos:
a3 + b3 = c6 ou a3 + b3 = (c2)3 (Equação de Fermat)
a5 + b5 = c10 ou a5 + b5 = (c2)5 (Equação de Fermat)
E assim por diante.
2º Caso: x = y = 2n e z múltiplo de x e y.
Exemplos:
a4 + a4 = c8 ou a4 + b4 = (c2)4 (Equação de Fermat)
a6 + b6 = c12 ou a6 + b6 = (c2)6 (Equação de Fermat)
E assim por diante.
3º Caso: x = 2n + 1, y = 2x e z = 3x.
Exemplos:
a3 + b6 = c9 ou a3 + (b2)3 = (c3)3 (Equação de Fermat)
a5 + b10 = c15 ou a5 + (b2)5 = (c3)5 (Equação de Fermat)
E assim por diante.
4º Caso: x = 2n , y = 2x e z = 3x.
Exemplos:
a4 + b8 = c12 ou a4 + (b2)4 = (c3)4 (Equação de Fermat)
a6 + b12 = c18 ou a6 + (b2)6 = (c3)6 (Equação de Fermat)
E assim por diante.