Propriedades Mecânicas: O Ensaio de Tração Uniaxial

PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Propriedades Mecânicas:
O Ensaio de Tração Uniaxial
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
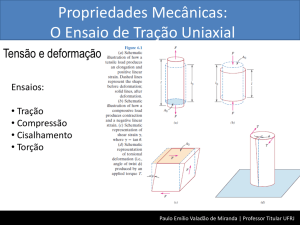
Tensão e deformação
Ensaios:
• Tração
• Compressão
• Cisalhamento
• Torção
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Tensão e deformação
Cálculo da tensão (Para tração e compressão):
Onde:
σ= Tens ão
F= Força normal à seção transversal
Ao= Área original da seção transversal
Cálculo da deformação (Para tração e compressão):
Onde:
∈= Deformação
li= Comprimento instantâneo
lo= Comprimento original
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Deformação Elástica
Resiliência
26/4/2011
Onde:
σ= Tens ão
E= Módulo de elasticidade (ou módulo de Young)
∈= Deformação
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Deformação Plástica
Tensão Limite de Escoamento
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Deformação Plástica
Localização da
Deformação plástica
através da estricção.
Tensão Limite de Resistência à Tração
Empescoçamento.
Critério de Considère
dσ/dε = σ
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Deformação Plástica
Ductilidade x Tenacidade
Onde:
%AL= Alongamento percentual
lf= Comprimento na fratura
lo= Comprimento original
Onde:
%RA= Redução de área percentual
Af = Área final
Ao = Área original
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Curvas de Tração para o Ferro
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Deformação Plástica: tensão verdadeira e deformação verdadeira
Tensão verdadeira
Deformação verdadeira
∈v
Onde:
σv = Tensão verdadeira
F= Força normal à seção transversal
Ai= Área instantânea da seção transversal
∈v = Deformação verdadeira
li= Comprimento instantâneo
lo= Comprimento original
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Propriedades Mecânicas
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Efeito do Sistema Deformante
• Um gráfico carga vs. deslocamento (Pi vs. ∆lTi) produzido por um
ensaio de tração é influenciado pela elasticidade do sistema
deformante;
• Entende-se por sistema deformante toda a região fora do
comprimento útil da amostra (l0), compreendendo parte do corpo
de prova, garras, travessão de aplicação de carga, etc;
• A influência da elasticidade do sistema (Ks) será tão maior quanto
menor for sua rigidez (resistência à deformãção elástica);
• Traçar uma curva tensão nominal vs. deformação nominal sem
excluir os valores elásticos do sistema deformante resulta em erros.
OBS: Exemplos baseados em resultados reais para um ensaio de tração
em uma liga de alumínio D16T.
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Gráfico Carga vs. Alongamento
1800
1600
1400
Pi (Kgf)
1200
1000
800
Carga vs. Deslocamento
600
400
200
(mm)
0
0
1
2
3
4
5
6
∆lTi(mm)
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Tratamento Matemático
(∆ l )
e+ p
a
∆lTi
i
Alongamento elástoplástico da amostra
Pi Pi lo
= ∆lTi − +
k s Ao E
Alongamento elastoplástico total
ε nie + p
Pi
ks
Alongamento elástico
total
Pi lo
Ao E
Alongamento elástico
da amostra
26/4/2011
(∆l )
e+ p
a
i
(
∆l )
=
e+ p
a
i
lo
Pi
σ ni =
Ao
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique
editar
o estilopara
do título
mestre
Curva
depara
Tração
Corrigida
o efeito
da elasticidade do
Sistema Deformante: Tensão x Deformação Nominal
600
Tensão (MPa)
500
400
300
Não corrigida
Corrigida
200
100
0
0,00
0,02
0,04
0,06
0,08
0,10
0,12
0,14
0,16
Deformação (%)
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Tensão Verdadeira vs. Deformação Verdadeira
• Uma vez que a deformação elástica não é
permanente, a deformação verdadeira é
considerada somente a parcela plástica da
deformação;
• Os valores são obtidos a partir da curva tensão
nominal vs. deformação nominal.
ε ni P
26/4/2011
Pi 
1
=  ∆lTi − 
lo 
ks 
ε vi = ln (ε ni P + 1)
σ vi = σ ni (ε ni P + 1)
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Tratamento Matemático
• A partir dos valores obtidos, obtem-se um
polinômio que melhor se ajuste à curva original;
• A partir desse polinômio, traça-se uma nova curva
tensão verdadeira vs. deformação verdadeira
ajustada;
• Os cálculos da cinética da deformação plástica são
obtidos a partir da curva ajustada.
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Comparação
• A seguir aparecem 3 exemplos práticos;
• A curva não corrigida – 1 – inclui as informações
elastoplásticas tanto da amostra quanto do sistema
deformante;
• Aplicando a correção, mas ainda deixando os
valores elásticos da amostra, gera a curva não
corrigida – 2 –;
• A curva corrigida leva em conta somente valores
plásticos.
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Comparação
Tensão Verdadeira (MPa)
700
600
500
400
300
200
Tensão Verdadeira vs. Deformação Verdadeira não corrigida 1
Tensão Verdadeira vs. Deformação Verdadeira não corrigida 2
Tensão Verdadeira vs. Deformação Verdadeira corrigida
100
0
0,00
0,02
0,04
0,06
0,08
0,10
0,12
0,14
0,16
Deformação Verdadeira (%)
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Tratamento Matemático
• Equações
empíricas
buscam
descrever
o
comportamento do material durante a deformação
plástica;
• São determinados matematicamente os estágios de
encruamento;
• As equações mais utilizadas são as de Hollomon,
Ludwig e Swift.
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Tratamento Matemático
• Hollomon - σ = Ken
– Normalmente descreve curvas que apresentam um único estágio de
encruamento;
– Em um gráfico logarítmico o traço é uma reta;
– K representa um coeficiente de resistência enquanto n é o expoente
de encruamento.
• Ludwig - σ = σ0 + Ken
– Descreve um ou mais estágios de encruamento;
– Em um gráfico logarítmico o traço é parabólico ou linear;
– σ0 representa uma tensão de escoamento.
• Swift - σ = K(ε+ ε0)n
– Descreve um ou mais estágios de encruamento;
– Em um gráfico logarítmico o traço é hiperbólico ou linear;
– ε0 representa uma deformação inicial.
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Obtenção dos Estágios de Encruamento
•
•
•
A partir da curva tensão verdadeira vs. deformação verdadeira ajustada, aplicar o
logarítimo nos dois eixos (Hollomon) e depois traçar a derivada (Ludwig e Swift);
Fazer ajustes lineares convenientes;
A partir das equações constitutivas linearizadas, identificar os valores de inclinação
(m) das retas ajustadas e de b.
Equação da reta: y – y0 = m(x – x0)
Hollomon linearizada: ln σ = ln K + n * ln ε
Ludwig derivada - linearizada: ln dσ/dε = ln(n*K) + (n-1)*ln ε
Swift derivada – linearizada:
ln dσ/dε = ln(n) + 1/n * ln(k) + ((n-1)/n) * ln (σ)
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Monocristais
III
τ
II
I
Estágio I – Deslizamento Fácil
Estágio II – Encruamento
Estágio III – Recuperação Dinâmica
γ
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Estágios de Encruamento
• Estágio I – Deslizamento Fácil
– Baixa densidade de discordâncias, logo, há pouca restrição à
movimentação das mesmas (não há interação entre discordâncias). A
tensão cresce muito pouco com a deformação;
• Estágio II – Encruamento
– A densidade de discordâncias aumenta muito rápido, as discordâncias
começam a interagir, encruando o material. A tensão cresce muito
com a deformação;
• Estágio III – Recuperação Dinâmica
– A densidade de discordâncias está próxima a de saturação, podendo
formar arranjos que minimizem a energia total do sistema (sub-grãos).
A tensão cresce menos com a deformação.
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Policristais
σn
III
II
SÓ POSSUEM OS ESTÁGIOS II E III
(em alguns casos apresentam um estágio
de comportamento semelhante ao de
deslizamento fácil e há estudos sobre
estágios IV e V em ensaios em
temperaturas elevadas)
εn
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Arranjos de Discordâncias
Estágio II
Estágio III
Encruamento Linear
Encruamento Parabólico
(concavidade negativa)
Pequeno alívio de tensão
Grande alívio de tensão
Estrutura Celular
Sub-grãos
Mais atuante em materiais de
elevada resistência mecânica
Mais atuante em materiais de
elevada ductilidade
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Dureza
• Resistência do material à deformação plástica localizada
• Dureza:
– Qualitativa:
• Mohs: Talco: 1; Diamante: 10
– Quantitativas:
• Uso de indentadores, carga aplicada com certa taxa
– Indentação: profundidade ou diâmetro
– Testes simples e rápido, não destrutivo, correlacionável
com parâmetros de tração e outros
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Técnicas de Medida de Dureza
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO UNIAXIAL
Clique para editar o estilo do título mestre
Escalas de Dureza
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
PROPRIEDADES MECÂNICAS: O ENSAIO DE TRAÇÃO
UNIAXIAL
9
10
8
Clique para editar o estilo do título mestre
Al2O3 + Fe, Ti, Cr
7
6
5
KAlSi3O8
4
2
Ca3(PO4)2(OH, F, Cl)
3
1
Al2SiO4(F,OH)2
26/4/2011
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ