Estruturas de Dados Estáticas – Cont.

Estruturas de Dados Estáticas – 1
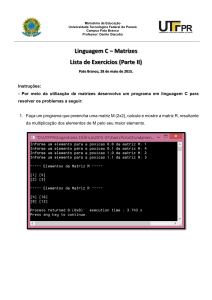
Estruturas de Dados Estáticas – Cont.
Matriz (arrays multidimensionais)
Uma matriz é uma variável composta homogênea bidimensional formada por
uma sequência de variáveis, todas do mesmo tipo, com o mesmo identificador (mesmo
nome) e alocadas sequencialmente na memória. Uma vez que as variáveis têm o mesmo
nome, o que as distingue são índices que referenciam sua localização dentro da
estrutura. Uma variável do tipo matriz é composta por linhas e colunas.
Estruturas indexadas que necessitam de mais de um índice para identificar um de
seus elementos são chamadas matrizes de dimensão n, onde n representa o número de
índices requeridos. Uma matriz de dimensão 2 é uma matriz que exige dois índices para
identificar um elemento em sua estrutura.
Exemplo: suponha que se necessite desenhar um gráfico de uma curva no plano
e que seja necessário guardar as posições dos pontos dessa curva em coordenadas x e y,
uma maneira possível de armazenar em memória o total dos pontos dessa curva seria na
forma de uma matriz de dimensão 2. Nela, um dado elemento conteria o valor
correspondente ao ponto identificado pelo índice de x para a abscissa e y para a
ordenada desse elemento.
Declaração de matriz
A declaração de uma matriz é muito semelhante à declaração de vetor.
Delimitadas entre os colchetes, temos duas declarações de tipo associadas aos índices,
separadas por uma vírgula. A convenção mais comum é dizermos que o primeiro índice
identifica uma linha de uma matriz bidimensional e o segundo, uma coluna.
DECLARE
NOME[LINHA, COLUNA] TIPO
Onde, nome é o nome da variável do tipo matriz, linha é a quantidade de
linhas que vão compor a matriz, coluna é a quantidade de colunas que vão compor a
matriz e tipo é o tipo de dados que poderá ser armazenado na sequência de variáveis
que formam a matriz.
DECLARE
VENDAS : VETOR [1..M, 1..N] DE INTEIROS
DECLARE
X : VETOR [3,5] DE INTEIROS
1 2 3 4 5
1
X
2
3
X[1,1]
X[3,4]
Exemplo de algoritmo para carregar uma matriz.
PARA i ← 1 ATÉ 3 FAÇA
INÍCIO
PARA j ← 1 ATÉ 5 FAÇA
INÍCIO
ESCREVA (“Digite o número da linha “, i, “ e
coluna “, j);
http://erinaldosn.wordpress.com
2 – Lógica de Programação
LEIA (X [i, j]);
FIM
FIM
Exemplo de algoritmo para mostrar os elementos de uma matriz.
PARA i ← 1 ATÉ 3 FAÇA
INÍCIO
PARA j ← 1 ATÉ 5 FAÇA
INÍCIO
ESCREVA (X[i, j];
FIM
FIM
Da mesma forma que se pode fazer operações com os elementos de um vetor, é
possível fazê-las com os elementos de uma matriz. É possível acessar individualmente
os elementos e, por conseguinte, os valores de cada uma das posições e realizar cálculos
matemáticos e comparativos, o que dá grande margem de possíveis aplicações
computacionais e práticas.
Exercícios
1. Faça um programa que carregue uma matriz 2 x 2, calcule e mostre uma matriz
resultante que será a matriz digitada multiplicada pelo maior elemento da matriz.
2. Faça um programa que carregue uma matriz 10 x 3 com as notas de dez alunos em
três provas. Mostre um relatório com o número do aluno (número da linha) e a
prova em que cada aluno obteve menor nota. Ao final do relatório, mostre quantos
alunos tiveram menor nota na prova1, quantos alunos tiveram menor nota na prova
2 e quantos alunos tiveram menor nota na prova 3.
3. Faça um programa que carregue:
Um vetor com oito posições com os nomes das lojas.
Um outro vetor com quatro posições com os nomes dos produtos.
Uma matriz com os preços de todos os produtos em cada loja.
O programa deve mostrar todas as relações (nome do produto – nome da loja) nas
quais o preço não ultrapasse R$ 120,00.
4. Faça um programa que carregue uma matriz 10 x 20 com números inteiros e some
cada uma das linhas, armazenando o resultado das somas em um vetor. A seguir,
multiplique cada elemento da matriz pela soma da linha e mostre a matriz resultante.
5. Faça um programa que carregue uma primeira matriz de ordem 4 x 5 e uma segunda
matriz 5 x 2, calcule e mostre a matriz resultante do produto matricial das duas
matrizes anteriores, armazenando-o em uma terceira matriz de ordem 4 x 2.
6. Faça um programa que carregue uma matriz 6 x 4 com números inteiros, calcule e
mostre quantos elementos dessa matriz são maiores que 30 e, em seguida, monte
uma segunda matriz com os elementos diferentes de 30. No lugar do número 30 da
segunda matriz coloque o número zero.
7. Faça um programa que carregue uma matriz 15 x 5 com números inteiros, calcule e
mostre quais os elementos da matriz que se repetem e quantas vezes cada um está
repetido.
8. Faça um programa que carregue uma matriz 10 x 10 com números inteiros, execute
as trocas especificadas a seguir e mostra a matriz resultante.
a linha 2 com a linha 8;
a coluna 4 com a coluna 10;
a diagonal principal com a diagonal secundária;
http://erinaldosn.wordpress.com
Estruturas de Dados Estáticas – 3
a linha 5 com a coluna 10.
9. Faça um programa que carregue uma matriz 8 x 8 com números inteiros e mostre
uma mensagem dizendo se a matriz digitada é simétrica. Uma matriz simétrica
possui A[i, j] = A[j, i].
10. Faça um programa que carregue:
Um vetor com os nomes de cinco produtos.
Uma matriz 5 x 4 com os preços dos cinco produtos em quatro lojas diferentes.
Um outro vetor com o custo do transporte dos cinco produtos.
Calcule uma segunda matriz 5 x 4 com os valores dos impostos de cada produto,
sendo que esses obedecem à tabela a seguir:
Preço
% de imposto
Até R$ 50,00
5
Entre R$ 50,01 e R$ 100,00
10
Acima de R$ 100,00
20
Mostre um relatório com o nome do produto, o número da loja onde o produto se
encontra, o valor do imposto a pagar, o custo de transporte, preço e o preço final
(preço acrescido do valor do imposto e do custo do transporte).
11. Faça um programa que receba:
Um vetor com o nome de cinco cidades diferentes.
Uma matriz 5 x 5 com a distância entre as cidades, sendo que na diagonal
principal deve ser colocada automaticamente distância zero, ou seja, não deve
ser permitida a digitação.
Calcule e mostre:
Os percursos que não ultrapassam 250 quilômetros (os percursos são compostos
pelos nomes das cidades de origem e pelos nomes das cidades de destino);
O consumo de um veículo, ou seja, quantos quilômetros o veículo faz por litro
de combustível e mostre um relatório com a quantidade de combustível
necessária para percorrer cada percurso citando o mesmo (nome da cidade de
origem e nome da cidade de destino);
A maior distância e em que percurso se encontra (nome da cidade de origem e
nome da cidade de destino).
12. Faça um programa que carregue:
Um vetor com cinco números inteiros.
Um outro vetor com dez números inteiros.
Uma matriz 4 x 3, também com números inteiros.
Calcule e mostre:
O maior elemento do primeiro vetor multiplicado pelo menor elemento do
segundo vetor. O resultado dessa multiplicação adicionado aos elementos
digitados na matriz dará origem a uma segunda matriz (resultante).
A soma dos elementos pares de cada linha da matriz resultante.
A quantidade de elementos entre 1 e 5 em cada coluna da matriz resultante.
13. Faça um programa que carregue uma matriz 7 x 7 de números inteiros e crie dois
vetores de sete posições cada um e que contenham, respectivamente, o maior
elemento de cada uma das linhas e o menor elemento de cada uma das colunas.
Escreva a matriz A e os dois vetores.
14. Faça um programa que utilize uma matriz 5 x 5 que aceite três tipos de valores:
múltiplo de 5, múltiplos de 11 e múltiplos de 13. Devem ser lidos apenas valores
maiores que zero. Após a leitura, os números devem ser distribuídos da seguinte
maneira:
http://erinaldosn.wordpress.com
4 – Lógica de Programação
Os múltiplos de 5 devem ocupar a diagonal principal;
Os múltiplos de 11 devem ficar acima da diagonal principal;
Os múltiplos de 13 devem ficar abaixo da diagonal principal.
Como alguns números podem ser múltiplos de 5, de 11 e também de 13, deve-se
primeiro verificar se o número digitado é múltiplo de 5. Caso não seja, deve-se
verificar se é múltiplo de 11. Caso não seja, deve-se verificar se é múltiplo de 13.
Caso não seja, deve-se mostrar a mensagem Número inválido.
Esse programa deve observar as seguintes situações:
Quando o usuário digitar um múltiplo de 5 e não houver mais espaço na
diagonal principal, mostre a mensagem Diagonal totalmente preenchida.
Quando o usuário digitar um múltiplo de 11 e não houver mais espaço
disponível na matriz, mostre a mensagem Não existe espaço acima da diagonal
principal.
Quando o usuário digitar um múltiplo de 13 e não houver mais espaço
disponível na matriz, mostre a mensagem Não existe espaço abaixo da diagonal
principal.
Quando a matriz estiver totalmente preenchida, mostre todos os elementos da
matriz, juntamente com suas posições (linha e coluna).
15. Faça um programa que utilize uma matriz com dimensões máxima de cinco linhas e
quatro colunas.
Solicite que sejam digitados os números que serão armazenados na matriz da
seguinte maneira:
Se o número digitado for par, deve ser armazenado em uma linha de índice par.
Se o número digitado for ímpar, deve ser armazenado em uma linha de índice
ímpar.
As linhas devem ser preenchidas de cima para baixo.
Quando não couberem mais números pares ou ímpares, deve ser mostrada uma
mensagem ao usuário.
Quando a matriz estiver totalmente preenchida, deve-se encerrar a leitura dos
números e mostrar todos os elementos armazenados na matriz.
16. Faça um programa que utiliza uma matriz com dimensões máxima de cinco linhas e
quatro colunas e solicite que sejam digitados os números (desordenadamente) e
armazene-os ordenadamente na matriz.
17. Faça um programa que utilize uma matriz com as dimensões fornecidas pelo usuário
e execute as solicitações a seguir:
A matriz deve ser obrigatoriamente quadrada (número igual de linhas e colunas).
Realize a leitura dos elementos que vão compor a matriz.
Some e mostre os elementos que estão abaixo da diagonal secundária.
18. Faça um programa que receba o estoque atual de três produtos que estão
armazenados em quatro armazéns e coloque esses dados em uma matriz 5 x 3.
Sendo que a última linha da matriz contém o custo de cada produto, calcule e
mostre:
A quantidade de itens armazenados em cada armazém.
Qual o armazém possui maior estoque do produto 2.
Qual o armazém possui menor estoque.
Qual o custo total de cada produto.
Qual o custo total de cada armazém.
19. Faça um programa que receba as vendas semanais (de um mês) de cinco vendedores
de uma loja e armazene essas vendas em uma matriz. Calcule e mostre:
http://erinaldosn.wordpress.com
Estruturas de Dados Estáticas – 5
O total de vendas do mês de cada vendedor.
O total de vendas de cada semana (todos os vendedores juntos).
O total de vendas do mês.
20. Faça um programa que:
Receba dez nomes de produtos e armazene-os em um vetor.
Receba o estoque desses dez produtos em cada um dos cindo armazéns (matriz 5
x 10).
Receba o custo dos dez produtos e armazene-os em um outro vetor.
Calcule e mostre:
O total de itens armazenados em cada armazém.
O total de itens armazenados de cada produto.
O custo total de cada armazém.
O nome do produto e o número do armazém que possui maior número de itens
estocados.
O nome do produto que possui menor custo.
Bibliografia
Fundamentos da Programação de Computadores
Ana Fernanda Gomes Ascencio, Edilene Aparecida Veneruchi de Campos
São Paulo: Pearson Prentice Hall
Lógica de programação e estrutura de dados, com aplicações em Java
Sandra Puga, Gerson Rissetti
São Paulo: Pearson Prentice Hall, 2009
Estrutura de dados e algoritmos em Java
Michael Goodrich, Roberto Tamassia
Porto Alegre: Bookman, 2007
http://erinaldosn.wordpress.com