INF1009.3WB: Lógica para computação - Aula 13: A - PUC-Rio

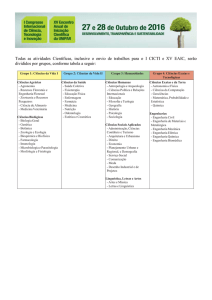
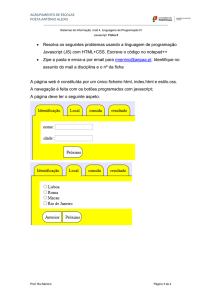
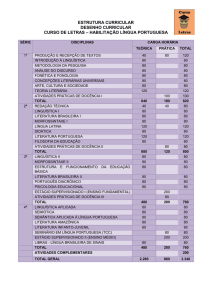
INF1009.3WB: Lógica para computação
Aula 13: A sintaxe da lógica de primeira ordem (cont.)
Cecília Englander
Guilherme F. Lima
Edward Hermann
Lab. TecMF, Dep. Informática, PUC-Rio
2017.1
INF1009.3WB: Lógica para computação, 2017.1
• Guilherme F. Lima ([email protected])
• Prof.: http://www.telemidia.puc-rio.br/~gflima/inf1009
• Disc.: http://www.tecmf.inf.puc-rio.br/LGRAD
Programa
P1: Lógica proposicional
• Formalização
• Sintaxe
• Semântica (tabela-verdade)
• Tableaux
P2: Lógica de primeira ordem (i)
• Formalização
⇒ Sintaxe
• Tableaux
P3: Lógica de primeira ordem (ii)
• Teoria dos conjuntos (básico)
• Semântica (estruturas)
Sumário
1. Aula passada
2. Definições de predicados
3. Formalização de argumentos
1/9
Sintaxe da lógica de primeira ordem
Alfabeto Símbolos lógicos e não-lógicos
Expressões Sequências finitas de símbolos do alfabeto
Termos Expressões que denotam objetos
Fórmulas Expressões que potencialmente possuem valor de verdade
Sentenças Fórmulas sem variáveis livres
Pergunta. Variável livre vs. ligada?
Pergunta. Fórmula vs. sentença?
2/9
Problema
Formalize em AE as seguintes sentenças
• x é primo
• Há pelo menos um número primo
• Há exatamente um número primo
• Há pelo menos dois números primos
• Há exatamente dois números primos
3/9
Definições de predicados
Toda fórmula ϕ com n variáveis livres define uma relação Rϕ (n-ária) no
universo tal que
Rϕ (x1 , . . . , xn )
sse ϕ(x1 , . . . , xn )
Exemplos
• Zero(x) := x = 0
AE
• Div(x, y) := ∃z(x × y = z)
AE
• Vazio(x) := ∀y¬(y ∈ x)
Sets
• Sub(x, y) := ∀z(z ∈ x → z ∈ y)
Sets
Pergunta. O que acontece se ligarmos todas variáveis livres que
ocorrem nos exemplos anteriores?
4/9
Notação (:=)
Vamos escrever
R(x1 , . . . , xn ) := ϕ(x1 , . . . , xn )
para indicar que R(x1 , . . . , xn ) é uma abreviação sintática da fórmula ϕ em
que as ocorrências de variáveis livres aparecem substituídas por x1 , . . . , xn
Exemplo (AE)
Se Div(x, y) := ∃z(x × z = y) então
• Div(0, 0) é uma abreviação para ∃z(0 × z = 0)
• Div(0, S(0)) é uma abreviação para ∃z(0 × z = S(0))
• Div(x, x) é uma abreviação para ∃z(x × z = x)
Pergunta. Qual a diferença entre =, ≡, e :=?
5/9
Exercício
Considere a linguagem de primeira ordem People tal que
• Igualdade: Sim
• Símbolos de predicado: Homem1 , Mulher1
• Símbolos de função: pai1 , mãe1
Defina os predicados
• Irmão(x, y): “ x é irmão de y”
• FilhoÚnico(x): “ x é filho único”
• Tia(x, y): “ x é tia de y”
• Prima(x, y): “ x é prima de y”
• Ancestrali (x, y): “ x é ancestral de nível i de y”
Pergunta. É possível definir simplesmente Ancestral(x, y)?
6/9
Formalização de argumentos
Informalmente
Um argumento é um conjunto de proposições em que uma delas é a
conclusão e as demais são premissas (que justificam a conclusão)
Formalmente
Vamos escrever
{ϕ1 , ϕ2 , . . . , ϕn } ` ψ
para indicar que é possível deduzir (provar) a conclusão ψ a partir do
conjunto de premissas {ϕ1 , . . . , ϕn }
Exemplo (AE)
{ ∀x(x > 0 → S(x) > 0), S(0) > 0 } ` S(S(0)) > 0
7/9
Exercícios
1. Brian estuda linguística. Brian pertence ao clube de xadrez. Portanto,
Brian estuda linguística e pertence ao clube de xadrez.
2. Alguém estuda linguística. Alguém pertence ao clube de xadrez. Então,
alguém estuda linguística e pertence ao clube de xadrez.
3. Todo sólido é solúvel em algum líquido. Portanto, existe um líquido em que
todo sólido é solúvel.
4. Apenas os secretários e administradores são elegíveis para o prêmio Desk
Clean. Ian é elegível para o prêmio Desk Clean. Portanto, Ian é um
secretário e um administrador.
5. Tudo que existe é material. Portanto, exatamente uma das seguintes
afirmações é verdadeira: (i) nada é material ou (ii) algumas coisas
materiais são mentais, e todas as coisas mentais são materiais.
8/9
Exercícios
6. Há um homem na cidade que faz a barba de todos os homens da cidade
que não barbeiam a si mesmos. Portanto, existe um homem na cidade que
se barbeia sozinho.
7. Cavalos são animais. Portanto, cabeças de cavalos são cabeças de animais.
8. A raiz quadrada de um quadrado perfeito é um número natural. Nenhum
número natural é uma fração. A raiz quadrada de um número natural que
não seja um quadrado perfeito não é uma fração. Por conseguinte, a raiz
quadrada de um número natural não é uma fração.
9. Se ninguém contribui para a Oxfam, em seguida, há alguém que morre de
fome. Portanto, há uma pessoa que morre de fome, se ele ou ela não
contribui para a Oxfam.
9/9
Fim