Teorema de Carnot

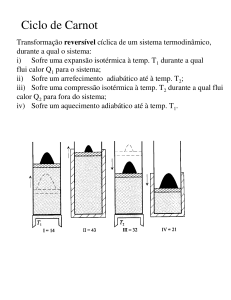
Teorema de Carnot
De todas as máquinas térmicas que funcionam entre duas
determinadas fontes de calor, a que tem rendimento máximo é a
máquina de Carnot.
Frig.
Q1 − Q2
Q1
>
Q1 * − Q2 *
Q1 *
e
Q1 − Q2 = Q1 * − Q2 *
Corolário do Teorema de Carnot
ou
Segundo Teorema de Carnot
Todas as máquinas de Carnot funcionando entre as mesmas
fontes de calor têm o mesmo rendimento, independentemente
da substância operante.
A escala de temperaturas termodinâmicas
(ou absolutas ou escala de Kelvin)
η=
Q1 − Q2
Q1
= 1−
Q2
Q1
Máq. de Carnot:
|Q1| / |Q2| é independente da natureza da
substância operante (2º Teorema de Carnot), só pode ser função da
temperatura (absoluta) das 2 fontes de calor.
Além disso, pode provar-se que só pode ser
Q1
Q2
=
f (T1 )
f (T2 )
Ou seja, o calor trocado com as fontes de calor do ciclo de Carnot
é uma boa propriedade termométrica e é independente do sistema
(termómetro) utilizado.
Podemos então definir uma escala de temperaturas absolutas,
fazendo operar uma máquina de Carnot entre uma fonte à temperatura
do ponto triplo e uma fonte à temperatura T:
T = 273 ,16
Q
Q3
(K )
Utilizando a escala de temperaturas absolutas, a temp. das fontes quente
e fria do ciclo de Carnot é
T1 = 273 ,16
Q1
(K )
Q3
Q1
Q2
=
T1
T2
e
T2 = 273 ,16
⇒ η Carnot = 1 −
Q2
Q3
T2
T1
(K )
Escala de temperaturas termodinâmicas idêntica à
escala de temperaturas do gás perfeito
T → temperatura na escala termodinâmica
Tg → temperatura na escala do gás perfeito:
PV=nRTg
P
Tg = 273,16 lim  
P3 →0 P
 3 V
Proc. isotérmicos
Q1 = −W1 = nRT1g ln
Q1
V4
V1
Q2 = −W2 = nRT 2 g ln
V2
V3
Proc. adiabáticos
Q2
T1V4
γ −1
γ −1
T1V1
 V4 V3
⇒
=
γ −1 
V1 V2
= T2V2 
= T2V3
γ −1
Q1
Q2
=
nRT1g ln(V4 / V1 )
nRT 2 g ln(V3 / V2 )
=
T1g
T2 g
Tg = cT
Mas visto que as duas escalas de temperatura foram definidas usando o
ponto triplo como ponto fixo,
T3 g = T3 = 273,16
⇒
 c =1

Tg = T
Num ciclo de Carnot:
i)
ii)
Q1 + Q2 + W = 0
Q1
Q2
=
Logo,
(Conservação da energia interna)
T1
Q
T
⇔ 1 = 1
T2
− Q2 T2
Q1 Q2
+
=0
T1 T2
O que significa?
Algum princípio de
conservação?
Enunciado do Teorema de Clausius
- S é um sistema termodinâmico que realiza uma transformação cíclica;
- Q1, Q2, ..., Qn são as quantidades de calor trocadas entre S e n
fontes de calor às temperaturas T1, T2, ...Tn, respectivamente;
- Qi > 0, se S recebe calor; Qi < 0 se S perde calor
Tn
T1
T2
Q1
Qn
n
Q2
S realiza uma
transformação
Q3
cíclica
Q5
T5
Q4
T3
T4
Qi
≤0
∑
i =1 Ti
ciclo
n
Qi
≤0
∑
i =1 Ti
ciclo
A soma dos calores recebidos ou cedidos pelo sistema S,
tomados com os respectivos sinais, e divididos pelas temperaturas
absolutas das fontes de calor que os cederam ou receberam, é
sempre negativa ou nula, i.e.,
A igualdade na expressão anterior só se verifica se os processos
que constituem o ciclo forem todos reversíveis.
No caso de o sistema ser posto em contacto com um número infinito de
fontes de calor, com cada uma das quais o sistema troca um calor
infinitesimal dQ, então a Igualdade e Desigualdade de Clausius tomam a
forma:
δQ
∫T
fonte
≤0
Nota: caso das máquinas térmicas
Fonte quente
Para uma máquina que utilize apenas 2 fontes
de calor e que não seja reversível:
Q1
Máquina
térmica
Q2
Fonte fria
W
η = 1−
Q1
Q2
Logo,
rendimento da máquina de
Carnot
< 1−
T1
|Q | T
⇔ 1 > 1
T2
| Q2 | T2
Q1 Q2
+
<0
T1 T2
i) Ciclo reversível: pode ser percorrido num ou noutro sentido sem
que se alterem os valores numéricos dos calores (e trabalhos)
trocados, apenas os seus sinais algébricos.
δQd
∫T
Para o ciclo percorrido num certo sentido, d
≤0
Para o ciclo percorrido no sentido inverso, e
fonte
δQe
∫T
≤0
fonte
δQe = −δQd
 δQd
≤0
∫ T

⇒  fonte
⇒
δQd
∫
≥0
 T fonte
δQd
∫T
=0
fonte
Além disso, para que cada transferência de calor seja reversível,
Tfonte = T onde T é a temperatura do sistema.
∫
δQrev
T
=0
Igualdade de Clausius,
válida para um ciclo reversível
ii) Ciclo irreversível: pelo menos um dos processos que constituem
o ciclo deu-se irreversivelmente. Pode acontecer, por
exemplo, que na troca de calor com a fonte i Ti ≠ T. Nesse
caso deve ser Ti a aparecer na desigualdade de Clausius.
δQirrev
∫T
fonte
<0
Desigualdade de Clausius,
válida para um ciclo irreversível
A entropia como função de estado
Processos reversíveis:
R1, R2 → caminhos (processos)
reversíveis
Igualdade de Clausius
Força generalizada, Y
↓
∫
δQrev
R1 R2
T
f
=
∫
R1 i
δQrev
T
i
+
∫
R2 f
δQrev
T
Deslocamento generalizado, X
f
∫
R1 i
δQrev
T
f
=
∫
δQrev
R2 i
→ Integral independente do caminho
T
⇓
Entropia, S
f
S f − Si =
∫
R i
δQrev
T
qualquer que seja o
caminho reversível R
=0
Variação infinitesimal de entropia:
dS =
δQrev
T
1/T é o factor integrante de δQrev
Processos irreversíveis:
R → caminho reversível
I → caminho irreversível
Força generalizada, Y
Desigualdade de Clausius
↓
δQirrev
∫T
IR
fonte
f
=
δQirrev
∫T
I i
fonte
i
+
∫
δQrev
T
1
424
3
R f
Si − S f
Deslocamento generalizado, X
f
S f − Si >
∫T
I i
Processos infinitesimais:
dS >
δQirrev
δQirrev
T fonte
fonte
<0
Princípio da Não Diminuição da Entropia
Processos reversíveis
f
δQ
S f − Si = ∫ rev
123 R i T
; δQrev = 0 ⇒ ∆S = 0
∆S
Processos irreversíveis
f
S f − Si > ∫
123 I i
∆S
δQirrev
T
; δQirrev = 0 ⇒ ∆S > 0
Logo, num processo adiabático qualquer
Princípio da não diminuição da entropia ou
Lei do aumento da entropia
Processos infinitesimais:
dS adiab ≥ 0
∆S adiab ≥ 0