Capítulo 7: Associação de Resistores

Capítulo 7: Associação de Resistores
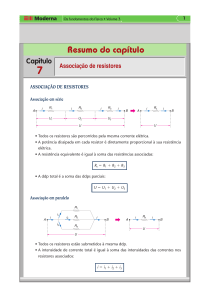
Os resistores podem ser associados basicamente de
dois modos distintos: em série e em paralelo. Ambos
os modos de associação podem estar presentes:
temos um associação mista.
Capítulo 7: Associação de Resistores
7.1 – Resistor equivalente. Associação dos resistores
em série.
7.2 – Associação de resistores em paralelo.
7.3 – associação mista de resistores.
7.4 – Curto circuito.
7.1 – Associação de resistores em série.
Objetivos:
• Analisar a associação de resistores em série.
• Compreender como obter a resistência do resistor
equivalente.
• Compreender o que é reostato e funcionamento.
• Analisar situação na qual o efeito Joule é
desejável: fios, fusíveis e lâmpadas
incandescentes.
7.1 – Associação de resistores em série.
Termos e conceitos:
• Resistor equivalente
• Disjuntor
• Potência nominal de uma lâmpada.
7.1 – Associação de resistores em série.
Dentre as muitas funções que já vimos sobre os
resistores surge a necessidade de valores de
resistência que não são fabricados ou não estão
disponíveis no momento, a solução então é associar
os resistores disponíveis para alcançar nosso
objetivo, com o valor de resistência equivalente.
7.1 – Associação de resistores em série.
Na associação em série os resistores são ligados um
em seguida do outro, de modo a serem percorridos
pela mesma corrente elétrica. Veja:
7.1 – Associação de resistores em série.
Vamos analisar esse sistema em termos de energia.
A potencia consumida por cada resistor pode ser
dada por:
2
𝑃𝑜𝑡1 = 𝑅1 . 𝑖
2
𝑃𝑜𝑡2 = 𝑅2 . 𝑖
2
𝑃𝑜𝑡3 = 𝑅3 . 𝑖
E como ficaria a potencia total consumida pelo
sistema?
7.1 – Associação de resistores em série.
𝑃𝑜𝑡 = 𝑃𝑜𝑡1 + 𝑃𝑜𝑡2 + 𝑃𝑜𝑡3
Agora podemos propor a resistência equivalente
2
2
2
𝑅𝑆 . 𝑖 = 𝑅1 . 𝑖 + 𝑅2 . 𝑖 + 𝑅3 . 𝑖
Simplificando:
𝑅𝑆 = 𝑅1 + 𝑅2 + 𝑅3
2
7.1 – Associação de resistores em série.
Se multiplicarmos a lei de Ohm para a associação
proposta teremos:
𝑅𝑆 . 𝑖 = 𝑅1 . 𝑖 + 𝑅2 . 𝑖 + 𝑅3 . 𝑖
Ou seja:
𝑈 = 𝑈1 + 𝑈2 + 𝑈3
7.1 – Associação de resistores em série.
Temos quatro resultados importantes. Em uma
associação de resistores em série:
• A potência dissipada em cada resistor é diretamente
proporcional à sua resistência elétrica.
• A resistência do resistor equivalente é igual à soma
das resistências dos resistores associados.
• A ddp em cada resistor é diretamente proporcional à
sua resistência elétrica.
• A ddp da associação em série é igual às somas das
ddps nos resistores associados.
7.1 – Associação de resistores em série.
7.1.2 – Reostatos.
São resistores cuja resistência elétrica pode ser
ajustada.
7.1 – Associação de resistores em série.
7.1.2 – Reostatos.
7.1.1 e 7.1.2 – exercícios.
7.1.1 e 7.1.2 – exercícios.
7.1.1 e 7.1.2 – exercícios.
7.1.1 e 7.1.2 – exercícios.
7.1.1 e 7.1.2 – exercícios.
7.1.1 e 7.1.2 – exercícios.
7.1.1 e 7.1.2 – exercícios.
7.1.1 e 7.1.2 – exercícios.
7.1.1 e 7.1.2 – exercícios.
7.1.1 e 7.1.2 – exercícios.
7.1.3 – Aplicação do efeito Joule
Em alguns momentos o efeito Joule configura um
problema, em outros, possível que esse efeito seja
desejado, como exemplo o funcionamento de
aquecedores elétricos, fusíveis e lâmpadas
incandescentes.
7.1.3 – Aplicação do efeito Joule
Fusíveis:
São dispositivos que tem a finalidade de proteger
circuitos elétricos. São constituídos basicamente de
materiais condutores cujo ponto de fusão é
relativamente baixo.
7.1.3 – Aplicação do efeito Joule
Fusíveis:
7.1.3 – Aplicação do efeito Joule
7.1.3 – Aplicação do efeito Joule
7.1.3 – Aplicação do efeito Joule
Disjuntores:
É uma chave magnética ou termomagnética que se
desliga automaticamente quando a intensidade da
corrente elétrica ultrapassa determinado valor.
7.1.3 – Aplicação do efeito Joule
Disjuntores:
7.1.3 – Aplicação do efeito Joule
Lâmpada incandescente:
É constituída de um fio de tungstênio denominado
filamento, cuja temperatura de fusão é muito alta,
cerca de 3400 ºC.
7.1.3 – exercícios
7.1.3 – exercícios
7.1.3 – exercícios
7.1.3 – exercícios
7.1.3 – exercícios
7.2 – associação em paralelo
Vários resistores são ligados em paralelo quando são
ligados pelos terminais de modo a ficarem
submetidos à mesma ddp.
7.2 – associação em paralelo
Pela Lei dos nós:
𝑖 = 𝑖1 + 𝑖2 + 𝑖3
Pela lei de Ohm.
𝑈 = 𝑖. 𝑅𝑃
𝑈1 = 𝑖1 . 𝑅1
𝑈2 = 𝑖2 . 𝑅2
𝑈3 = 𝑖3 . 𝑅3
7.2 – associação em paralelo
Sabe-se que U = 𝑈1 = 𝑈2 = 𝑈3
Temos então:
𝑈
𝑅𝑃
=
𝑈
𝑅1
+
𝑈
𝑅2
+
𝑈
𝑅3
1
1
1
1
=
+
+
𝑅𝑃 𝑅1 𝑅2 𝑅3
7.2 – associação em paralelo
Temos quatro observações importantes. Em uma
associação em paralelo:
• A intensidade de corrente é igual à soma das
intensidades das correntes nos resistores associados.
• O produto da resistência elétrica de cada um deles
pela respectiva corrente é igual para todos os
resistores.
• A corrente elétrica em cada resistor é inversamente
proporcional à sua resistência elétrica.
• O inverso da resistência equivalente é igual à soma
dos inversos das resistências associadas.
7.2 – associação em paralelo
Casos particulares de associação em paralelo:
• Dois resistores:
1
𝑅𝑃
=
1
𝑅1
+
1
𝑅2

1
𝑅𝑃
=
𝑅1 +𝑅2
𝑅1 .𝑅2
 𝑅𝑃 =
• Vários resistores iguais:
𝑅
𝑅𝑃 =
𝑛
𝑅1 𝑅2
𝑅1 +𝑅2
7.2 – associação em paralelo
Do ponto de vista energético:
Em uma associação de resistores em paralelo, a
potência dissipada em cada resistor é inversamente
proporcional à sua resistência elétrica.
2
2
2
𝑈
𝑈
𝑈
𝑃𝑜𝑡1 =
; 𝑃𝑜𝑡2 =
; 𝑃𝑜𝑡3 =
𝑅1
𝑅2
𝑅3
7.2 – Exercícios
7.2 – Exercícios
7.2 – Exercícios
7.2 – Exercícios
7.2 – Exercícios
7.2 – Exercícios
7.2 – Exercícios
7.2 – Exercícios
7.2 – Exercícios
7.2 – Exercícios
7.2 – Exercícios
7.2 – Exercícios
.
7.2 – Exercícios
.
7.3 – Associação mista de resistores
Objetivo:
• Analisar a associação mista de resistores.
Termos e conceitos
• Nós
• Terminais de uma associação de resistores
7.3 – Associação mista de resistores
São as associações constituídas por associações em
paralelo e associações em série.
Qualquer associação mista pode ser substituída por
um resistor equivalente.
7.3 – Associação mista de resistores
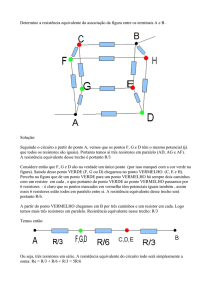
Para determinar a resistência equivalente em uma
associação é muito útil designar os nós e os
terminais da associação por letras.
7.3 – Associação mista de resistores
• Nós: são os pontos em que a corrente se divide.
• Terminais: são os pontos entre os quais se quer
determinar a resistência equivalente.
7.3 – Associação mista de resistores
Simplifica-se aos poucos o esquema resolvendo as
associações em que os resistores estejam
claramente em série (um depois do outro, sem
ramificação) ou em paralelo (ligados aos mesmos
pontos).
7.3 – Associação mista de resistores
Atenção: durante o processo não podem
desaparecer os terminais da associação.
7.3 – Exercícios
7.3 – Exercícios
7.3 – Exercícios
7.3 – Exercícios
7.3 – Exercícios
7.3 – Exercícios
7.3 – Exercícios
7.3 – Exercícios
7.3 – Exercícios
7.3 – Exercícios
7.3 – Exercícios
7.3 – Exercícios
7.3 – Exercícios
7.3 – Exercícios
7.3 – Exercícios
7.3 – Exercícios
7.3 – Exercícios
.
7.3 – Exercícios
.
7.3 – Exercícios
.
7.3 – Exercícios
.
7.3 – Exercícios
.
7.3 – Exercícios
.
7.3 – Exercícios
.
7.3 – Exercícios
.
7.3 – Exercícios
.