Função

C
Sistema destinado à preparação para
Concursos Públicos e Aprimoramento Profissional via
INTERNET
www.concursosecursos.com.br
RACIOCÍNIO LÓGICO
AULA 06
RELAÇÕES E FUNÇÕES
Par Ordenado
O par ordenado representa um ponto do sistema de eixos cartesianos. Este
sistema é composto por um par de retas perpendiculares.
A reta horizontal é chamada de eixo x, eixo das abscissas ou Ox.
A reta vertical é o eixo y, eixo das ordenadas ou Oy.
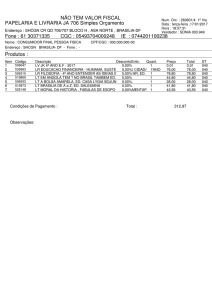
Os eixos x e y dividem o plano em quadrantes numerados conforme mostra a
figura:
y
2º quadrante
1º quadrante
x
4º quadrante
3º quadrante
Representação do par ordenado
Um ponto P é representado pelo par ordenado (m, n), portanto, as coordenadas
de P são (m, n), ou ainda, a abscissa de P é m e sua ordenada é n. Da mesma forma
qualquer ponto do plano cartesiano está associado a um único par ordenado.
y
P(3, 2)
2
P(m, n)
3
ordenada
x
IETAV System- CGC: 03.755.533/0001-71
[email protected]
abscissa
-
Fone/Fax:
(24)
3360-0011
C
Sistema destinado à preparação para
Concursos Públicos e Aprimoramento Profissional via
INTERNET
www.concursosecursos.com.br
Igualdade de pares ordenados
Dizemos que dois pares ordenados são iguais se possuírem abscissas e ordenadas
iguais.
(a, b) = (r, s) ⇒ a = r e b = s
Teste o que aprendeu
1. Localizar no plano cartesiano os pontos (1, 0), (-2, 4), (-3, 1), (3, -1) e (0,
2).
2. Determine a e b para que: (a + 1, 2b + 3) = (0, 12)
Produto Cartesiano
Chama-se produto cartesiano de A por B (A × B) ao conjunto de pares
ordenados onde as abscissas são pontos de A e as ordenadas são pontos de B.
Exemplo:
Sejam os conjuntos A = {0, 3, 5}, B={1, 7}
A × B = {(0, 1), (0, 7), (3, 1), (3, 7), (5, 1), (5, 7)}
Analogamente temos:
B × A = {(1, 0), (1, 3), (1, 5), (7, 0), (7, 3), (7, 5)}
Observe que:
A×B≠B×A
Observe também que A tem 3 elementos, B tem 2 elementos e A × B tem 6
elementos. De forma geral, para dois conjuntos quaisquer vale:
n(A × B) = n(A) ⋅ n(B)
IETAV System- CGC: 03.755.533/0001-71
[email protected]
-
Fone/Fax:
(24)
3360-0011
C
Sistema destinado à preparação para
Concursos Públicos e Aprimoramento Profissional via
INTERNET
www.concursosecursos.com.br
Teste o que aprendeu
1. Sendo A = {-2, 0, 1} e B = {1, 3, 4} determine:
a. A × B
b. B × A
c. A × A
2. O conjunto A × B tem 21 elementos, A tem 3 elementos. Quantos
elementos possui B?
Relação
Considera-se relação de A em B todo subconjunto de A × B que obedece a uma
lei de formação.
Exemplo:
Sejam os conjuntos A = {0, 3, 5}, B={1, 7}
A × B = {(0, 1), (0, 7), (3, 1), (3, 7), (5, 1), (5, 7)}
Vamos determinar o conjunto R ⊂ A × B tal que x < y, onde x é a abscissa e y é
a ordenada:
R = {(0, 1), (0, 7), (3, 7), (5, 7)}
Observe que os pares ordenados (3, 1) e (5, 1) ficaram de fora porque não
obedeciam à lei de formação(x <y).
Função
Função matemática é uma relação de A em B em que, para todo x em A temos
um único y em B, onde x e y obedecem a uma lei de formação.
Nos diagramas a seguir identificamos algumas funções:
IETAV System- CGC: 03.755.533/0001-71
[email protected]
-
Fone/Fax:
(24)
3360-0011
C
Sistema destinado à preparação para
Concursos Públicos e Aprimoramento Profissional via
INTERNET
www.concursosecursos.com.br
1
b
2
c
3
É função, pois cada elemento de A
está associado e um único
elemento de B e não sobram
elementos em A.
a
a
1
b
2
c
3
Não é função, pois o elemento d ∈
A não está associado e nenhum
elemento de B
d
a
1
b
2
É função, pois cada elemento
de A está associado a algum
elemento de B e não sobram
elementos em A.
c
a
1
b
2
c
3
Não é função pois a ∈ A está
associado a dois elementos
distintos em B.
Domínio, Imagem e Contradomínio
Consideremos os conjuntos A = {0, 1, 2} e B = {0, 1, 2, 3, 4, 5}.
A função f : A → B definida por y = x + 1 ou f(x) = x + 1 tem como diagrama:
IETAV System- CGC: 03.755.533/0001-71
[email protected]
-
Fone/Fax:
(24)
3360-0011
C
Sistema destinado à preparação para
Concursos Públicos e Aprimoramento Profissional via
INTERNET
www.concursosecursos.com.br
•0
0•
•1
B
•2
1•
A
•3
2•
•4
•5
Define-se:
•
•
•
O conjunto A é denominado domínio da função, que é indicado por D.
No exemplo acima D = {0, 1, 2}.
O conjunto {1, 2, 3}, que é um subconjunto de B, é denominado conjunto
imagem da função, que indica-se por Im = {1, 2, 3}.
O conjunto B, tal que Im ⊂ B, é denominado contradomínio da função.
Observe que:
f(0) = 1
f(1) = 2
f(2) = 3
Exemplo:
Dados os conjuntos A = {-3, -1, 0, 2} e B = {-1, 0, 1, 2, 3, 4}, determinar o conjunto imagem
da função f : A → B definida por f(x) = x +2.
Resolução:
f(-3) = (-3) + 2 = -1
f(-1) = (-1) + 2 = 1
f(0) = 0 + 2 = 2
f(2) = 2 + 2 = 4
Portanto: Im = {-1, 1, 2, 4}
IETAV System- CGC: 03.755.533/0001-71
[email protected]
-
Fone/Fax:
(24)
3360-0011
C
Sistema destinado à preparação para
Concursos Públicos e Aprimoramento Profissional via
INTERNET
www.concursosecursos.com.br
Teste o que aprendeu
Considerando o diagrama seguinte, que representa uma função de A em B, determine o que
se pede:
a)
b)
c)
d)
e)
f)
D
f(-1)
f(0)
f(2)
Im
A lei de formação
Estudo do domínio de uma função
Quando definimos uma função, o domínio D, que é o conjunto de todos os
valores possíveis da variável independente x, pode ser dado explicita ou implicitamente.
Assim:
•
f(x) = 2x –5, com 1 ≤ x ≤ 10, está explicito que o domínio da função consiste em
todos os números reais entre 1 e 10: D = { x ∈ ℜ ⏐ 1 ≤ x ≤ 10}
•
f(x) = 2x – 5, sem explicitar o domínio D, está implícito que x pode ser qualquer
número real, ou seja, D = ℜ.
•
2x − 3
, sem explicitar o domínio D, está implícito que
x−2
qualquer número real, com exceção de 2, pois se x = 2, teremos:
f(x) =
x pode ser
2(2) − 3 1
= , o que não é definido.
2−2
0
Portanto: D = { x ∈ ℜ ⏐ x ≠ 2}
f(2) =
•
f(x) = x − 2 , sem explicitar o domínio, está implícito que (x – 2) pode ser
qualquer número real não-negativo, ou seja, x – 2 ≥ 0 ou x ≥ 2.
D = { x ∈ ℜ ⏐ x ≥ 2}
IETAV System- CGC: 03.755.533/0001-71
[email protected]
-
Fone/Fax:
(24)
3360-0011
C
Sistema destinado à preparação para
Concursos Públicos e Aprimoramento Profissional via
INTERNET
www.concursosecursos.com.br
Teste o que aprendeu
Determine o domínio D da função definida por:
f ( x) =
x
x −5
f ( x) =
x
2x − 1
f ( x) = 2 x + 1
Função par e função impar
Considere a função f(x) = x2 + 2.
f(1) = 12 + 2 = 3
f(-1) = (-1)2 + 2 = 3
f(2) = 22 + 2 = 6
f(-2) = (-2)2 + 2 = 6
f(1) = f(-1) = 3
f(2) = f(-2) = 6
Função par: ∀ x ∈ ℜ, f(x) = f(-x)
Considere f(x) = 5x.
f(1) = 5 × 1 = 5
f(-1) = 5 × (-1) = -5
f(2) = 5 × 2 = 10
f(-1) = 5 × (-2) = -10
f(1) = -f(-1) = 5
f(2) = -f(-2) = 10
Função impar: ∀ x ∈ ℜ, f(x) =- f(-x)
Função crescente e função decrescente
IETAV System- CGC: 03.755.533/0001-71
[email protected]
-
Fone/Fax:
(24)
3360-0011
C
Sistema destinado à preparação para
Concursos Públicos e Aprimoramento Profissional via
INTERNET
www.concursosecursos.com.br
y aumenta
Observe o gráfico:
y2
y1
x1
x2
x aumenta
Note que aumentando o valor de x, o valor de y também aumenta. As funções
que possuem esta característica são chamadas de crescentes.
Função crescente: ∀ x1 ∈ ℜ, ∀ x2 ∈ ℜ, x2 > x1 ⇒ f(x2) > f(x1)
y diminui
Observe o gráfico:
y2
y1
x1
x2
x aumenta
Função decrescente: ∀ x1 ∈ ℜ, ∀ x2 ∈ ℜ, x2 > x1 ⇒ f(x2) < f(x1)
Funções sobrejetora, injetora e bijetora
Função sobrejetora:
Uma função é sobrejetora quando seu conjunto imagem é o próprio
contradomínio. Em outras palavras, não “sobram” elementos no contradomínio.
IETAV System- CGC: 03.755.533/0001-71
[email protected]
-
Fone/Fax:
(24)
3360-0011
C
Sistema destinado à preparação para
Concursos Públicos e Aprimoramento Profissional via
INTERNET
www.concursosecursos.com.br
a
1
b
2
c
Função Injetora
Uma função é injetora se para cada dois elementos distintos do domínio temos
duas imagens diferentes no contradomínio: x1 ≠ x2 ⇒ f(x1) ≠ f(x2).
a
1
4
b
2
a
1
b
2
c
3
4
5
c
3
É injetora
5
Não é injetora
Função bijetora
As funções que são ao mesmo tempo injetoras e sobrejetoras são denominadas
funções bijetoras. Portanto, elementos distintos do domínio possuem imagens
diferentes, e o contradomínio é igual ao conjunto imagem.
a
1
b
2
c
3
Função inversa
Toda função bijetora possui a sua inversa, ou seja, se f é uma aplicação de A em
B, sua inversa será uma aplicação de B em A.
IETAV System- CGC: 03.755.533/0001-71
[email protected]
-
Fone/Fax:
(24)
3360-0011
C
Sistema destinado à preparação para
Concursos Públicos e Aprimoramento Profissional via
INTERNET
www.concursosecursos.com.br
f
0
1
1
2
2
3
f: A → B
f(0) = 1; f(1) = 2; f(2) = 3
f -1
0
1
1
2
2
3
f -1: B → A
f(1) = 0; f(2) = 1; f(3) = 2
Os pares ordenado de f são (0, 1), (1, 2), (2, 3) e os de f –1 são (1, 0), (2, 1),
(3, 2), as abscissas de f são as ordenadas de f –1, e as ordenadas de f são as abscissas de
f –1. Portanto para determinar a função inversa basta substituir a abscissa x pela
ordenada y. Observe:
f: A → B
f(x) = x + 1 ou y = x + 1
substituindo x por y temos:
x=y+1
y = x – 1 , por tanto a função inversa de f é f –1(x) = x – 1
Teste o que aprendeu
1. Determinar a função inversa de f(x) = 6x + 2
2. Determinar a função inversa de f(x) = x3 – 1
3. Determinar a função inversa de f(x) =
x −1
2x
Função Composta
Considere duas funções f e g tal que f: A → B e g: B → C, conforme o
diagrama:
IETAV System- CGC: 03.755.533/0001-71
[email protected]
-
Fone/Fax:
(24)
3360-0011
C
Sistema destinado à preparação para
Concursos Públicos e Aprimoramento Profissional via
INTERNET
www.concursosecursos.com.br
g
f
h
Queremos determinar uma única função h : A → C que realize as mesmas
operações que f e g.
Esta função deve levar um elemento do conjunto A diretamente para C, sem
passar por B. A função h, assim determinada, será chamada de função composta.
Notação: h(x) = gοf(x) = g(f(x))
Para determinar a função composta g(f(x)), devemos, na função g, substituir x
por f(x) e resolver as operações necessárias.
Exemplo:
Sejam f: ℜ → ℜ onde f(x) = x + 1 e g: ℜ → ℜ onde g(x) = 2x.
Determinar h(x) = gοf(x)
Queremos determinar h(x) = gοf(x) = g(f(x)), portanto na função g substituímos
x pela função f(x:
g(x) = 2x ⇒ g(f(x)) = 2 × f(x) = 2 × (x + 1) = 2x + 2
Portanto:
h(x) = 2x + 2
Teste o que aprendeu
Dadas as funções definidas em ℜ → ℜ tais que: f(x) = x3 + 1 e g ( x) =
x
,
2
determine:
1) fοg(x)
2) gοf(x)
3) (gοf) -1(x)
IETAV System- CGC: 03.755.533/0001-71
[email protected]
-
Fone/Fax:
(24)
3360-0011
C
Sistema destinado à preparação para
Concursos Públicos e Aprimoramento Profissional via
INTERNET
www.concursosecursos.com.br
Testes
1) Considere os conjuntos A e B tais que A × B = {(-1, 0), (2, 0), (-1, 2), (2, 2), (-1, 3),
(2, 3)}. O número de elementos de A ∩ B é:
a) 0
b) 1
c) 2
d) 3
e) 4
2) Se A = {0, 1, 2} e B = {0, 2, 4, 5} então o número de elementos distintos do
conjunto (A × B) ∪ (B × A) é:
a) 4
b) 8
c) 12
d) 20
e) 24
3) Uma função f de variável real satisfaz a condição f(x + 1) = f(x) + f(1), qualquer que
seja o valor da variável x. Sabendo-se que f(2) = 1, podemos concluir que f(5) é igual a:
a) 1/2
b) 1
c) 5/2
d) 5
e) 10
1
4) Seja f a função definida por f(x) = 2x3 – 1. Então f(0) + f(-1) + f( ) é:
2
− 19
− 17
−3
− 15
a)
b)
d)
c)
4
4
4
4
5) Qual das funções a seguir é par?
1
a) f(x) = 2
x
b) f(x) =
d)
c) f(x) = x
e) nenhuma das anteriores
e)
− 13
4
1
x
f(x) = x5
6) Seja a função f(x) = ax3 + b. Se f(-1) = 2 e f(1) = 4, então a e b valem,
respectivamente:
a) –1 e –3
b) –1 e 3
c) 1 e 3
d) 3 e –1
e) 3 e 1
7) Sejam f dada por f(x) = 2x – 1 e g dada por g(x) = x + 1. Então g(f(2)) é igual a:
a) 1
b) 2
c) 3
d) 4
e) 5
8) Se f(x) = a + 1 e g(z) = 2z + 1, então g(f(x)) vale:
a) 2a + 2
b) a + 4
d) 2a + 3
e) a + 3
9) A função inversa da função f(x) =
c) 2a – 3
2x − 1
é:
x+3
IETAV System- CGC: 03.755.533/0001-71
[email protected]
-
Fone/Fax:
(24)
3360-0011
C
Sistema destinado à preparação para
Concursos Públicos e Aprimoramento Profissional via
INTERNET
www.concursosecursos.com.br
x+3
2x − 1
1 − 2x
c) f −1 (x) =
3− x
3x + 1
e) f −1 (x) =
2− x
2x + 1
x −3
3x − 1
d) f −1 (x) =
x−2
a) f −1 (x) =
b) f −1 (x) =
10) Numa seqüência, têm-se que f(1) = 4 e f(n+1) = 2f(n) – 1. Determine o valor de
f(3).
a) 13
b) 10
c) 8
d) 7
e) 5
Gabarito dos testes
1
B
2
D
3
C
4
C
5
A
6
C
IETAV System- CGC: 03.755.533/0001-71
[email protected]
7
D
-
8
D
Fone/Fax:
9
E
(24)
10
A
3360-0011