t φ , N t φ ε BA φ θ ˆ n B B ˆ n B B

1 ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE TEORIA Neste tópico apresentamos os princípios básicos de transformação de energia mecânica em energia elétrica, os quais são fundamentados na Lei de indução de Faraday. Quer a energia elétrica venha do vento ou da água, da força nuclear ou do carvão, das ondas ou das marés, ela é gerada de acordo com o princípio da indução eletromagnética. Dínamos
(alternadores)
Energia mecânica
Energia elétrica
Fontes primárias de energia mecânica:
•Represas de água (Hidroelétricas)
•Combustíveis fósseis: gás, petróleo, carvão
(Termoelétricas)
•Fissão nuclear (Nuclear)
•Sol (Energia solar)
•Vento (Eólica)
•Ondas e Marés
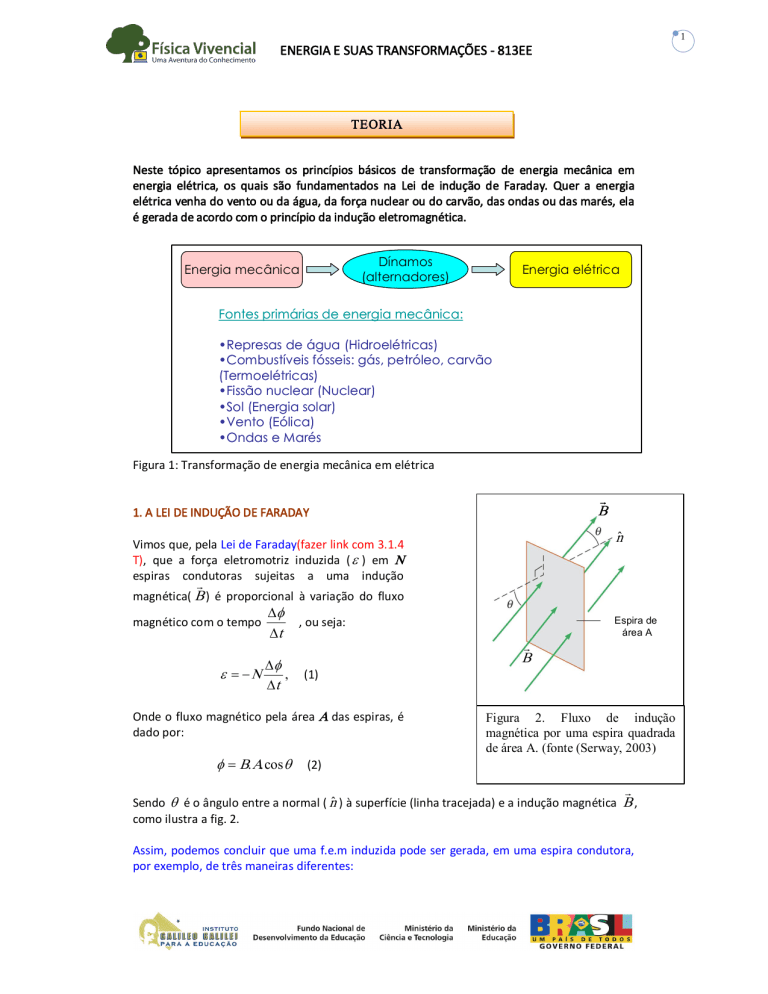
Figura 1: Transformação de energia mecânica em elétrica r B 1. A LEI DE INDUÇÃO DE FARADAY ˆ n Vimos que, pela Lei de Faraday(fazer link com 3.1.4 T), que a força eletromotriz induzida ( e ) em N espiras condutoras sujeitas a uma indução r magnética( B ) é proporcional à variação do fluxo magnético com o tempo e = - N Df
D t
, ou seja: r Df
, (1) D t
Onde o fluxo magnético pela área A das espiras, é dado por: f = B. A.cos q
Espira de área A B Figura 2. Fluxo de indução magnética por uma espira quadrada de área A. (fonte (Serway, 2003)
(2) r Sendo q é o ângulo entre a normal ( nˆ ) à superfície (linha tracejada) e a indução magnética B , como ilustra a fig. 2. Assim, podemos concluir que uma f.e.m induzida pode ser gerada, em uma espira condutora, por exemplo, de três maneiras diferentes: 2 ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE a) O condutor move‐se através de um campo magnético estacionário(somente a área A exposta ao campo varia no tempo). Este princípio se aplica nos geradores de corrente contínua, como mostram as figuras 3 a e 2 b. Neste caso, a fem induzida no circuito será: DA
(3) D t
e = - N.B. cos q . rr B (entrando no plano) ΔF (b) Figura 3. A figura ilustra uma espira retangular de área A = x.l , variável à medida que r
r
r
variamos x pelo deslocamento da barra (em azul). DF = I l ´ B é força de restauração que atua na barra( fonte Serway‐2003). r Como ilustra a figura 3a, para induzir uma corrente pelo circuito, aplicamos uma força ( F app ) sobre a barra móvel (em azul) que desliza sobre dois trilhos metálicos fixos separados pela distância l . Um resistor R (considerado como a resistência equivalente do circuito), fecha o circuito para circular e limitar a corrente I induzida (indicada no sentido convencional). Assim, a velocidade com que a barra se desloca na direção x , é dada por: Ú =
Dx . D t
A variação D x é ilustrada na figura 2 b. Assim, a força eletromotriz induzida é dada por: e = - N.B. cos q .
DA
Dx = - (1) .B. cos(0o ).l. Dt
Dt e = - B.l . Ú
Onde A = x.l , é a área da espira, que varia com x . Esta tensão contínua induzida (fixa no tempo) é ilustrada no circuito elétrico equivalente na figura 4. 3 ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE (4) Figura 4. Circuito elétrico equivalente à figura 2, ou seja, a barra em movimento equivale a um gerador elétrico. O sentido da corrente é invertido se a barra se mover na direção oposta, ou seja, se diminuirmos a distância x. ( fonte Serway‐2003). Uma vez que a resistência do circuito é R, a corrente que circula é dada por: I=
ε B lv
= R R (5) Pela conservação da energia, a potência gerada (em Watts) é igual a potência dissipada no resistor R, dada por: P= Fapp v= ( I lB ) v =
ε 2 (gerada) (5)
R ou, P= RI 2 =
(Bl v ) 2 (dissipada) R (6) Mas ainda permanece uma questão: Porque é gerada uma corrente pela barra quando a movimentamos num campo magnético uniforme? Podemos observar pela figura 5, que os elétrons na barra estão sujeitos a uma força (de Lorentz) dada por: r
r r
FB = qv × B (7) dirigida ao longo da barra. Sob a influência desta força, os elétrons movem‐se para a extremidade inferior do condutor(barra) onde se acumulam. Como efeito da separação de cargas, negativa e positiva, que se deslocam em sentido contrário, é gerado um campo elétrico no condutor. As cargas se acumulam nas extremidades do condutor até que exista um r
r r
r r
equilíbrio entre a força elétrica FE = qE e a força magnética FB = qv × B sobre os portadores de carga, negativa e positiva. Em módulo temos: qv B= qE Þ E=v B
(8) 4 ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE Figura 5. Deslocamento de elétrons em um condutor devido a sua movimentação sob a ação r de um campo B uniforme. ( fonte Serway‐2003). Obviamente, com a existência deste campo elétrico, também coexiste uma diferença de potencial entre as extremidades do condutor enquanto este se mover através do campo magnético uniforme. Se a direção do movimento é invertida, a diferença de potencial também é invertida. Daí, o esquema elétrico equivalente, ilustrado na figura 4, ou seja a barra equivale a um gerador. Fechando o circuito, como mostrado na figura 3, os elétrons (de carga q=­e) fluem pelos fios, ou pelos trilhos no sentido real indicado pela força de Lorentz (F B). Em um circuito elétrico, adotamos o sentido da corrente (sentido convencional), como sendo o sentido do fluxo dos portadores de carga positiva pelo circuito. b) A espira gira em um campo magnético estacionário. Este princípio se aplica nos geradores de corrente alternada, por exemplo. D( cos q ) (9) D t
e = - N.AB . . espira nˆ q
r B coletores r B Rotor externo Circuito externo w
escovas 5 ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE Figura 6. Gerador de tensão alternada. Note que q = wt , onde w é a freqüência angular de rotação da espira(fonte ‐ Serway ‐ 2003). r Como podemos observar na figura 6, o ângulo q , formado entre o campo B e a norma ( nˆ ) à área (A) da espira, varia quando a espira (armadura) gira com uma freqüência angular w . Como efeito, é induzida na espira uma f.e.m que oscila, entre positiva e negativa, no tempo. Veremos adiante, no tópico "Dínamos e geradores de corrente alternada”, que os geradores de corrente elétrica de alta energia obtêm a corrente elétrica por indução eletromagnética; e que nesses geradores, para se produzir variação do fluxo, fazem‐se espiras girar num campo magnético estacionário. Pois bem, para que a variação de fluxo por segundo seja grande, isto é, para que o fluxo varie rapidamente, ou que D( cos q ) seja elevado, essas espiras devem D t
executar em geral, 50 ou 60 rotações por segundo. Suponhamos o quadro(espira quadrada) ABCD plano, girando com movimento de rotação r uniforme de velocidade w em um campo magnético uniforme de indução magnética B . Sabemos que, numa posição do quadro na qual a sua normal faz com o campo um ângulo q , o fluxo que atravessa a área A do quadro vale: f = B. A.cos q
(10) À medida que o quadro gira, varia o ângulo q , e, portanto o fluxo f . Há, então, indução no quadro e aparece no condutor uma corrente elétrica i, como mostra a figura 7. q nˆ Figura 7‐ Corrente (i) induzida em uma espira quadrada que gira com uma velocidade angular r w sob a ação de uma indução magnética B . (fonte: http://efisica.if.usp.br/eletricidade/basico/inducao/inducao_quadro_plano_rot_c_unifor/) É muito importante exprimirmos a variação do fluxo em função do tempo, à medida que o quadro gira. Para isso, comecemos a contar o tempo de rotação do quadro no instante em que q = 0o . Nesse caso, num instante t qualquer, o ângulo q vale q = wt . E o fluxo, nesse instante, é expresso por : f = B. A.cos(wt ) (11)
6 ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE A figura 8 mostra como varia o fluxo magnético f com a freqüência angular w e com o tempo t. θ
θ Figura 8. Variação do fluxo com o deslocamento angular q = wt e com o tempo. T é o período da oscilação, T =
2p
w
. (fonte: http://efisica.if.usp.br/eletricidade/basico/inducao/inducao_quadro_plano_rot_c_unifor/) b1. Força eletromotriz induzida no quadro Como: D( cos w t ) D t
e = - N.AB . . (12) a espira plana gira com movimento de rotação uniforme dentro de um campo magnético uniforme e a força eletromotriz induzida na espira é uma função alternada no tempo. Uma força eletromotriz desse tipo é chamada, por definição, força eletromotriz alternada. Para obtermos uma elevada f.e.m. é necessário que a espira gire muito depressa, ou seja, que efetue um grande número de rotações em um intervalo de tempo ( D t ) extremamente pequeno. Nestas condições, ou seja, no limite quando D t tende a zero, a variação D( cos w t ) , D t
resulta em uma operação que veremos somente no ensino superior, que é conhecida como a derivada de uma função e que neste caso particular, é definida por: logo: d (cos w t ) = - w senw t dt
7 ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE e = N.AB
. .w
senwt ou e = e max senwt
(13) Como e max = NABw é constante, vemos que a f.e.m. induzida é diretamente proporcional a senw t e a velocidade angular w da espira. Portanto, para obtermos grande f.e.m. é necessário que o quadro gire muito depressa. Conclusões Quando um quadro plano gira com movimento de rotação uniforme dentro de um campo magnético uniforme, a força eletromotriz induzida no quadro é uma função senoidal do tempo. Uma força eletromotriz desse tipo é chamada, por definição, força eletromotriz alternada senoidal. A representação gráfica de e em função de t é mostrada na figura está na figura 9. e e( t ) = ( N.AB
. .w ) senwt
N.ABw
. . e max
e min
T = 2p w
­N.ABw
. . Figura 9. Representação do sinal da f.e.m induzida na espira em função do tempo. (fonte: http://efisica.if.usp.br/eletricidade/basico/inducao/inducao_quadro_plano_rot_c_unifor/) b2. Corrente induzida no quadro Seja R a Resistência dos condutores que formam o quadro, alimentado pela f.em. induzida e , então a corrente induzida no quadro (veja fig. 10) é dada por: 8 ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE I =
e
R ou I = NAB w
senw t R
NABw
constante, essa expressão mostra que I é diretamente proporcional a R
senw t . O valor máximo da corrente é aquele para o qual senwt = 1 , evidentemente o valor mínimo da corrente é obtido quando senw t = - 1 . Sendo I m ax = Podemos escrever : I = Im ax senw t (14) Conclusões 1 a ) A corrente elétrica induzida no quadro é uma função senoidal do tempo. Uma corrente desse tipo é chamada corrente alternada senoidal. A representação gráfica de I em função de t está indicada na figura 9. Essa corrente é chamada alternada, porque ela percorre o condutor ora num sentido, ora noutro. A figura abaixo indica o seguinte: que a corrente no início tem valor zero; vai aumentando, até atingir um máximo em T/4; depois vai diminuindo até se anular em T/2; depois muda de sentido e vai aumentando até atingir um máximo em 3T/4; depois vai diminuindo, até se anular em T; muda de sentido novamente, e reinicia o ciclo. I + I (t ) = (
NABw
R
NAB w
) senwt R
I m ax
I m inin - NABw
R
Figura 10. Representação do sinal da corrente induzida pela espira em função do tempo. (fonte: http://efisica.if.usp.br/eletricidade/basico/inducao/inducao_quadro_plano_rot_c_unifor/) 9 ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE Vemos que o tempo T que a corrente demora para realizar um ciclo completo é igual ao tempo T que o quadro demora em dar uma volta no campo magnético. Na corrente usada na cidade de São Paulo esse tempo T é de 1/60 segundo, isto é, a corrente muda de sentido 60 vezes por segundo. Na corrente usada no Rio de Janeiro, esse tempo T é de 1/50 segundo. NAB w
senw t (15), que a corrente R
induzida também é diretamente proporcional à velocidade angular w do quadro. Isso está de 2 a ) Como era de se esperar, vemos pela fórmula I = acordo com a lei de Faraday: a corrente induzida será tanto maior quanto mais rápida for a variação do fluxo. Também fica evidente, que a corrente induzida, será tanto maior quanto maior for o número de espiras N, sua área A e a intensidade da indução magnética B. b3) Valor eficaz O valor eficaz de uma corrente alternada periódica é o valor I ef de uma corrente contínua constante que, num intervalo de tempo igual a um período, dissipa a mesma energia em um mesmo resistor. No caso da corrente alternada pode‐se demonstrar que: I ef = I max
2 (16) O conceito de valor eficaz é estendido à tensão alternada. No caso de uma tensão alternada senoidal, de valor máximo U max , pode‐se demonstrar que o valor eficaz U ef dessa tensão é dado por: U U ef = max 2 Quando se diz que o a tensão entre os terminais de uma tomada é 110 volts, isso significa que o valor eficaz é de 110 volts. Portanto o valor máximo da tensão nessa tomada é: U m ax = U ef . 2 = 110. 2 Þ U ma x ; 155 volts Quando uma corrente alternada percorre um resistor, a potência média ( Pm ) dissipada nesse resistor é definida como a energia dissipada em um período, dividida pelo período. Pode‐se demonstrar que: Pm = U ef .I ef = R.( I ef ) 2 (17)
10 ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE Pois para um resistor, a equação: U = R. I
(18) Continua válida tanto para valores instantâneos como para valores eficazes. c) A espira permanece estacionária em um campo magnético variável no tempo. Este princípio se aplica nas bobinas das velas de ignição nos motores dos automóveis e também nos transformadores. e = - N.A .cos q
DB
D t
(19) Ex: Seja um anel de cobre de raio r numa região onde há um campo magnético variável no tempo (com módulo crescendo à taxa DB
), como ilustra a D t
figura 11. A variação de B faz aparecer (induz) uma corrente na espira. Portanto, um campo elétrico (E) induzido passa a existir na espira. Pode‐se então dizer que: um campo magnético variável no tempo produz um campo elétrico, também variável no tempo (Lei de Faraday reformulada). As linhas do campo elétrico induzido são tangentes ao anel, formando um conjunto de circunferências concêntricas. r Figura 11. O campo B (que penetra na folha), varia no tempo, gerando um campo elétrico r E no anel. (Serway­ 2003)
c1. Um exemplo deste efeito eletromagnético são as chamadas correntes de Focault. Nos itens anteriores, limitamo‐nos ao estudo de forças eletromotrizes induzidas em condutores com forma de fio e barras. Nesses casos, as correntes induzidas têm trajetórias bem definidas que são os próprios fios. No entanto, há situações em que o condutor é uma peça de dimensões maiores que um fio e nesses casos as correntes induzidas já não têm 11 ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE trajetórias bem definidas e são chamadas http://pt.wikipedia.org/wiki/Corrente_de_Foucault). correntes de Foucault. ( Suponhamos, por exemplo, que um bloco de ferro seja colocado com a face plana ABCD perpendicular a um campo magnético variável no tempo, como mostra a figura 12. Sendo A, a área dessa face, ela é atravessada por um fluxo f = AB
. . Se o campo for variável no tempo, então o fluxo magnético será variável no tempo. Neste caso, o bloco de ferro sofrerá indução eletromagnética e aparecerão nele correntes elétricas induzidas circulares, geradas pelo campo elétrico circular induzido no bloco. Estas correntes circulam em planos perpendiculares r à indução magnética B , isto é, em planos paralelos a ABCD. Figura 12. Um campo magnético variável produz um campo elétrico. a) Bloco de ferro sujeito a r uma indução magnética B variável no tempo. b) Bloco de ferro constituído de vária lâminas. (Fonte: http://efisica.if.usp.br/eletricidade/basico/inducao/correntes_foucault/) Em alguns casos, como por exemplo, nos núcleos de motores elétricos, dínamos e transformadores, as correntes de Foucault são indesejáveis tanto pela dissipação de energia (provocando aquecimento das peças) como pelo fluxo magnético que elas mesmas criam. Nesses casos, as correntes de Foucault são também chamadas de correntes parasitas. Para reduzir as correntes parasitas, essas peças são construídas na forma de lâminas finas isoladas entre si por um verniz isolante ou Óxido de Ferro, de modo que as lâminas fiquem paralelas às linhas de indução (veja figura 12 b). Há casos, porém que as correntes de Foucault são úteis. O calor gerado por elas pode ser utilizado para fundir peças metálicas nos chamados fornos de indução. O forno de indução consiste basicamente de uma bobina percorrida por uma corrente alternada, com a peça metálica a ser fundida colocada no interior da bobina, como ilustra a figura 13
Material a ser fundido bobina Parede do forno do forno
12 ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE Figura 13. Esquema simplificado de um forno de indução. As correntes de Foucault são aproveitadas também na construção de freios magnéticos. Como mostra a figura 14, uma placa metálica oscilando entre os dois pólos de um eletroimã, gera uma variação do fluxo magnético através da placa. Essa variação do fluxo magnético através da placa fará, de acordo com a lei de indução de Faraday, surgir o aparecimento de uma corrente elétrica na própria placa. Estas correntes induzidas, que aparecem em circuitos fechados que oscilam em um plano perpendicular a um campo magnético são chamadas de corrente de Foucault, ou correntes parasitas. Esta corrente, por sua vez, também gera um campo magnético que se opõe ao campo magnético indutor (lei de Lenz), fazendo a placa parar de oscilar em pouco tempo. Para interromper a circulação de corrente parasita pelo pêndulo, basta recortá‐lo em tiras isoladas, como mostra a figura 14 b. Figura 14. Freio magnético Pendular. Esse princípio é utilizado em vários tipos de frenagens, entre elas podemos citar a frenagem de trens, de guinchos de grandes guindastes e até mesmo em carretilhas de pesca. Fonte: Serway‐2003. Em instrumentos tais como amperímetros e voltímetros analógicos são importante que o movimento do ponteiro seja rapidamente amortecido para que possamos fazer a leitura. Assim, o ponteiro a ser frenado leva um pequeno disco de metal que fica entre os pólos de um imã. Quando o ponteiro se move, o disco também se move e assim são geradas nele correntes de Foucault, as quais, de acordo com a Lei de Lenz, devem opor‐se a movimento, e assim o ponteiro é frenado. Conclusões importantes: n Um campo elétrico é gerado em um condutor como resultado da variação do fluxo magnético com o tempo; n Mesmo na ausência de um condutor, um campo magnético variável no tempo produzirá um campo elétrico no espaço vazio;
13 ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE n Este campo elétrico tem propriedades diferentes do que os campos produzidos por cargas estacionárias. 2. DÍNAMOS OU GERADORES MECÂNICOS DE ELETRICIDADE Chamam‐se geradores mecânicos de corrente elétrica, ou dínamos, aos dispositivos que transformam energia mecânica em energia elétrica. 1º ‐ Dínamo com corrente contínua É aquele que fornece corrente contínua, isto é, uma corrente que circula num único sentido. 2º ‐ Dínamo com corrente alternada (ALTERNADOR) Também chamado alternador – é aquele que fornece corrente alternada, isto é, corrente que circula num sentido e noutro alternadamente. 2.1. Princípio de funcionamento de Dínamos Os dínamos funcionam por meio de indução eletromagnética. E esta é sem dúvida a mais importante aplicação do fenômeno de indução de Faraday. Isso porque esse fenômeno é o único que fornece corrente elétrica com grande energia, como por exemplo, essa corrente que é fornecida para iluminação das cidades e para as indústrias. O princípio de funcionamento dos dínamos, tanto de corrente contínua como de corrente alternada, é a indução eletromagnética num quadro plano que gira num campo magnético uniforme. Tanto no dínamo de corrente alternada como no de corrente contínua o quadro é percorrido por corrente alternada. A diferença entre eles está na maneira de colher essa corrente para fora do quadro. Essa captação da corrente para fora do quadro é feita por um dispositivo chamado coletor. 2.1.a. Coletor de corrente alternada Na figura 15, consideramos que o quadro seja aberto em A e D, e daí sejam tirados dois condutores AB e CD que são ligados a dois anéis, B e D. Encostados a esses anéis existem dois pedaços de carvão (que é condutor), m e n. O circuito externo, R, onde vai ser utilizada a corrente, é ligado a esses pedaços de carvão. À medida que o quadro gira dentro do campo magnético(gerado entre os pólos do imã), os anéis giram juntos com ele. Os pedaços de carvão m e n ficam fixos e os anéis ficam raspando neles. A corrente que se produz no quadro passa para os anéis, deste para o carvão e do carvão vai para o circuito externo. É fácil ver que, com esse dispositivo, quando a corrente elétrica muda de sentido no quadro, também muda de sentido no circuito externo, isto é, no circuito externo ela é captada também como alternada, como ilustra a figura 17.a).
14 ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE Figura 15. Dínamo com coletor de corrente alternada. (fonte: http://efisica.if.usp.br/eletricidade/basico/inducao/dinamos/) Coletor é o nome que se dá ao conjunto dos anéis e pedaços de carvão (fig. 15). Os pedaços de carvão são chamados escovas. 2.1.b. Coletor de corrente continua – Dínamo com comutador Em vez de dois anéis ele se compõe de dois semi‐anéis. Cada semi‐anel é ligado a uma ponta do quadro girando junto com o quadro. Os pedaços de carvão são fixos, e são ligados ao circuito externo. Quando os semi‐anéis giram, os mesmos são pressionados contra os pedaços de carvão (figura 16). Vemos que, em cada meio período, um semi‐anel está em contato com um pedaço de carvão diferente.
15 ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE Figura 16. Dínamo com coletor de corrente contínua (com comutador) ( fonte: http://efisica.if.usp.br/eletricidade/basico/inducao/dinamos/) A posição dos carvões é ajustada de tal modo que, no instante em que a corrente muda de sentido no quadro, há troca de contato entre os carvões e os semi‐anéis. Desse modo, fora do quadro, a corrente caminha sempre no mesmo sentido, isto é, é contínua, como ilustra a figura 17 b. Tal corrente, cuja intensidade varia periodicamente mas cujo sentido se conserva, é denominada corrente pulsante. Acesse o sítio http://www.walter‐fendt.de/ph14br/generator_br.htm , para verificar como funciona um dínamo com comutador e sem comutador. Figura 17. Sinal de corrente gerada no circuito externo de um Dínamo: a)sem
comutador. b) com comutador.
Fonte: http://www.feiradeciencias.com.br/sala13/13_T02.asp.
16 ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE 3. AS USINAS ELÉTRICAS OU ESTAÇÕES GERADORAS Vimos que os dínamos consistem numa série de espiras que executam movimento de rotação uniforme num campo magnético uniforme. Essas espiras, para executarem movimento de rotação, necessitam de energia mecânica. De onde provém essa energia? Na prática, provém de energia térmica ou da energia de uma queda d’água, do vento, das marés ou das ondas. Tomemos como exemplo o caso da queda d’água. O aproveitamento de uma queda d’água para fornecer energia mecânica a um dínamo é feito do seguinte modo: armazena‐se a água de um ou de vários rios numa região muito vasta, chamada represa. A água dessa represa cai, pelo interior de tubos, de uma altura H , e vai acionar uma roda que possui na periferia certo número de pás como na figura (fig. 18). A energia com que a água chega às pás faz com que a roda execute movimento de rotação. A roda com as pás é chamada turbina. Figura 18. Energia mecânica gerada por queda d’água. (fonte: http://efisica.if.usp.br/eletricidade/basico/inducao/dinamos/) Ao eixo da turbina são ligados os condutores do dínamo, de maneira que, quando a roda gira, eles também giram. Vimos que a energia elétrica da corrente, isto é, a energia comunicada aos elétrons que se deslocam nos condutores provém da energia potencial (mecânica) da água que estava na represa. Ao conjunto do dínamo com turbina se chama usina hidroelétrica, ou estação geradora de eletricidade[ http://pt.wikipedia.org/wiki/Usina_hidrel%C3%A9trica]. Autor Gilberto Petraconi Filho. Mestrado e Doutorado em Física de Plasmas e Descargas Elétricas pelo ITA. Professor adjunto do Instituto Tecnológico de Aeronáutica (ITA). Vice‐chefe da Divisão de Ciências Fundamentais do ITA e Coordenador do Laboratório de Plasma e Processos do ITA.
17
ENERGIA E SUAS TRANSFORMAÇÕES ‐ 813EE