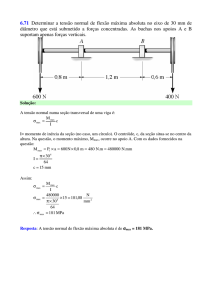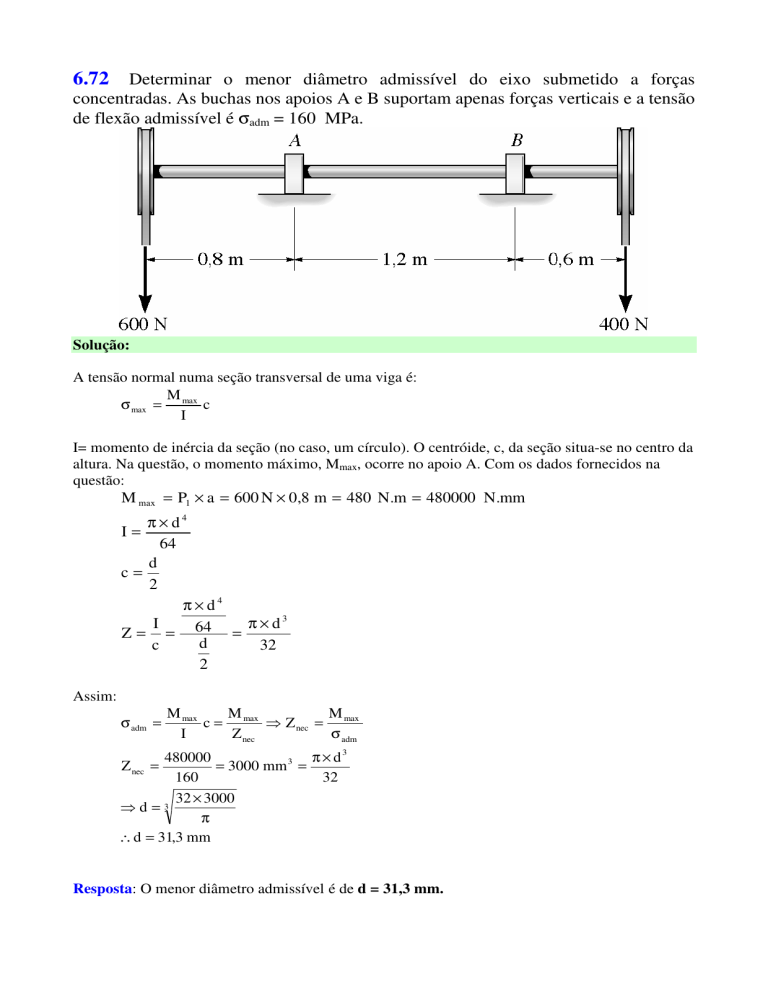
6.72 Determinar o menor diâmetro admissível do eixo submetido a

Propaganda

6.72 Determinar o menor diâmetro admissível do eixo submetido a forças
concentradas. As buchas nos apoios A e B suportam apenas forças verticais e a tensão
de flexão admissível é σadm = 160 MPa.
Solução:
A tensão normal numa seção transversal de uma viga é:
M
σ max = max c
I
I= momento de inércia da seção (no caso, um círculo). O centróide, c, da seção situa-se no centro da
altura. Na questão, o momento máximo, Mmax, ocorre no apoio A. Com os dados fornecidos na
questão:
M max = P1 × a = 600 N × 0,8 m = 480 N .m = 480000 N .mm
π× d4
64
d
c=
2
π× d4
I
π × d3
64
Z= =
=
d
c
32
2
I=
Assim:
σ adm =
M max
M
M
c = max ⇒ Z nec = max
I
Z nec
σ adm
480000
π × d3
= 3000 mm 3 =
160
32
32 × 3000
⇒d=3
π
∴ d = 31,3 mm
Z nec =
Resposta: O menor diâmetro admissível é de d = 31,3 mm.