MECÂNICA – TURMA UNP – PARTE 3 1. O gráfico mostra a

MECÂNICA – TURMA UNP – PARTE 3
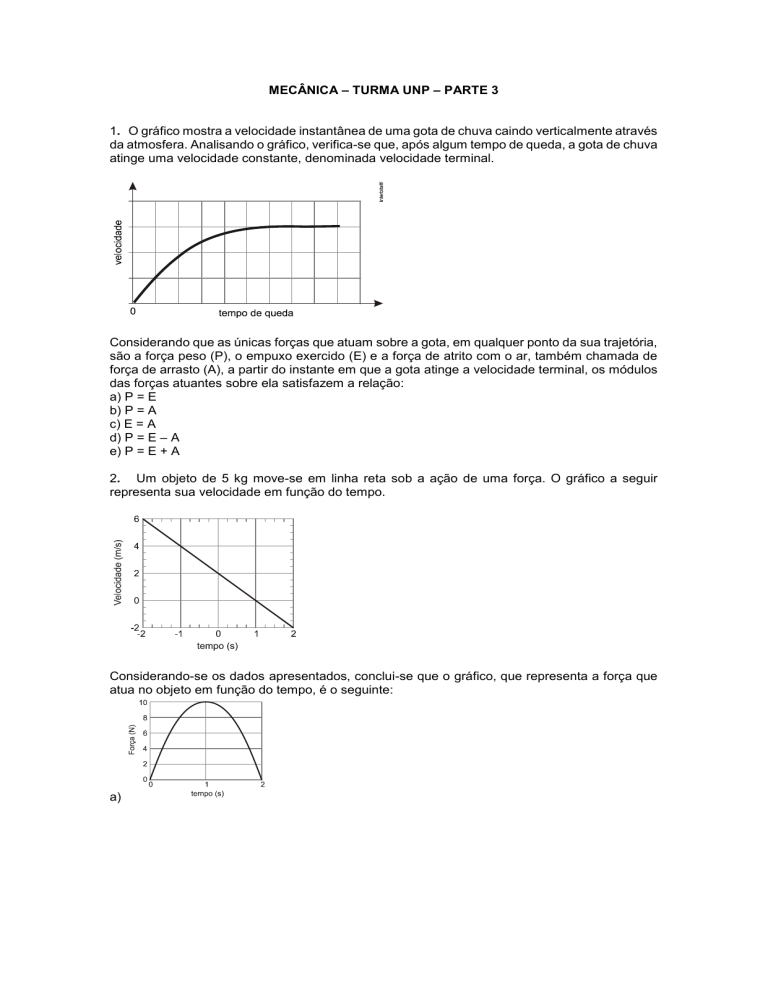
1. O gráfico mostra a velocidade instantânea de uma gota de chuva caindo verticalmente através
da atmosfera. Analisando o gráfico, verifica-se que, após algum tempo de queda, a gota de chuva
atinge uma velocidade constante, denominada velocidade terminal.
Considerando que as únicas forças que atuam sobre a gota, em qualquer ponto da sua trajetória,
são a força peso (P), o empuxo exercido (E) e a força de atrito com o ar, também chamada de
força de arrasto (A), a partir do instante em que a gota atinge a velocidade terminal, os módulos
das forças atuantes sobre ela satisfazem a relação:
a) P = E
b) P = A
c) E = A
d) P = E – A
e) P = E + A
2. Um objeto de 5 kg move-se em linha reta sob a ação de uma força. O gráfico a seguir
representa sua velocidade em função do tempo.
Considerando-se os dados apresentados, conclui-se que o gráfico, que representa a força que
atua no objeto em função do tempo, é o seguinte:
a)
b)
c)
d)
e)
3. Uma criança desliza em um tobogã muito longo, com uma aceleração constante. Em um
segundo momento, um adulto, com o triplo do peso da criança, desliza por esse mesmo tobogã,
com aceleração também constante. Trate os corpos do adulto e da criança como massas
puntiformes e despreze todos os atritos. A razão entre a aceleração do adulto e a da criança
durante o deslizamento é:
a) 1.
b) 2.
c) 1/3.
d) 4.
4. O corpo de um aspirador de pó tem massa igual a 2,0 kg. Ao utilizá-lo, durante um dado
intervalo de tempo, uma pessoa faz um esforço sobre o tubo 1 que resulta em uma força de
intensidade constante igual a 4,0 N aplicada ao corpo do aspirador. A direção dessa força é
paralela ao tubo 2, cuja inclinação em relação ao solo é igual a 60º, e puxa o corpo do aspirador
para perto da pessoa.
Considere sen 60° = 0,87, cos 60° = 0,5 e também que o corpo do aspirador se move sem atrito.
Durante esse intervalo de tempo, a aceleração do corpo do aspirador, em m/s 2, equivale a:
a) 0,5
b) 1,0
c) 1,5
d) 2,0
5.
Dois cubos de mesma densidade e tamanhos diferentes repousam sobre uma mesa
horizontal e mantêm contato entre si por uma de suas faces. A aresta de um dos cubos mede o
dobro da aresta do outro. Em um dado instante, uma força constante F, horizontal, é aplicada
sobre o cubo menor que, por sua vez, empurra o maior, conforme a figura a seguir.
Despreze todos os atritos. A razão entre o módulo de F e o módulo da força de contato entre os
cubos é:
a) 8.
b) 2.
c) 1/8.
d) 9/8.
6.
Roldanas móveis são utilizadas para vantagens mecânicas, ou seja, aplica-se uma
determinada força a uma extremidade do sistema e transmite-se à outra extremidade uma força
de maior intensidade. Esse tipo de recurso é comumente utilizado em guindastes de construção
civil para levantar materiais de grandes massas.
Um modelo semelhante ao dos guindastes está apresentado na figura, em que são colocadas 3
roldanas móveis e 1 fixa.
Considerando a massa M igual a 500 kg sendo levantada a partir do repouso em um local cuja
aceleração gravitacional é de 10 m/s2, podemos afirmar que, após 2 s, ela atingirá a velocidade,
em m/s, de:
a) 4.
b) 8.
c) 10.
d) 12.
e) 14.
7. O bungee jump é um esporte radical no qual uma pessoa salta no ar amarrada pelos
tornozelos ou pela cintura a uma corda elástica.
Considere que a corda elástica tenha comprimento natural (não deformada) de 10 m. Depois de
saltar, no instante em que a pessoa passa pela posição A, a corda está totalmente na vertical e
com seu comprimento natural. A partir daí, a corda é alongada, isto é, tem seu comprimento
crescente até que a pessoa atinja a posição B, onde para instantaneamente, com a corda
deformada ao máximo.
Desprezando a resistência do ar, é correto afirmar que, enquanto a pessoa está descendo pela
primeira vez depois de saltar, ela:
a) atinge sua máxima velocidade escalar quando passa pela posição A.
b) desenvolve um movimento retardado desde a posição A até a posição B.
c) movimenta-se entre A e B com aceleração, em módulo, igual à da gravidade local.
d) tem aceleração nula na posição B.
e) atinge sua máxima velocidade escalar numa posição entre A e B.
8. Para passar de uma margem a outra de um rio, uma pessoa se pendura na extremidade de
um cipó esticado, formando um ângulo de 30° com a vertical, e inicia, com velocidade nula, um
movimento pendular. Do outro lado do rio, a pessoa se solta do cipó no instante em que sua
velocidade fica novamente igual a zero. Imediatamente antes de se soltar, sua aceleração tem
Note e adote:
Forças dissipativas e o tamanho da pessoa devem ser ignorados.
A aceleração da gravidade local é g = 10 m/s2.
sen 30  cos 60  0,5
cos 30  sen 60  0,9
a) valor nulo.
b) direção que forma um ângulo de 30° com a vertical e módulo 9 m/s 2.
c) direção que forma um ângulo de 30° com a vertical e módulo 5 m/s2.
d) direção que forma um ângulo de 60° com a vertical e módulo 9 m/s 2.
e) direção que forma um ângulo de 60° com a vertical e módulo 5 m/s2.
9. Um avião voa numa trajetória retilínea e horizontal próximo à superfície da Terra. No interior
da aeronave, uma maleta está apoiada no chão. O coeficiente de atrito estático entre a maleta e
o chão do avião é μ e a aceleração da gravidade no local do voo é g. Considerando esta
situação, analise as seguintes afirmativas:
1. Se a maleta não se mover em relação ao chão do avião, então um passageiro pode concluir
corretamente, sem acesso a qualquer outra informação, que o avião está se deslocando com
velocidade constante em relação ao solo.
2. Se o avião for acelerado com uma aceleração superior a μg, então o passageiro verá a maleta
se mover para trás do avião, enquanto um observador externo ao avião, em repouso em relação
à superfície da Terra, verá a maleta se mover no mesmo sentido em que o avião se desloca.
3. Para um mesmo valor da aceleração da aeronave em relação à Terra, com módulo maior que
μg, maletas feitas de mesmo material e mesmo tamanho, mas com massas diferentes,
escorregarão no interior do avião com o mesmo valor da aceleração em relação ao chão da
aeronave.
Assinale a alternativa correta.
a) Somente a afirmativa 1 é verdadeira.
b) Somente a afirmativa 3 é verdadeira.
c) Somente as afirmativas 1 e 2 são verdadeiras.
d) Somente as afirmativas 2 e 3 são verdadeiras.
e) Somente as afirmativas 1 e 3 são verdadeiras.
10. Uma caixa, inicialmente em repouso, sobre uma superfície horizontal e plana, é puxada por
um operário que aplica uma força variando linearmente com o tempo. Sabendo-se que há atrito
entre a caixa e a superfície, e que a rugosidade entre as áreas em contato é sempre a mesma,
a força de atrito, no decorrer do tempo, está corretamente representada pelo gráfico:
a)
b)
c)
d)
e)
11. Um trabalhador da construção civil tem massa de 70 kg e utiliza uma polia e uma corda
ideais e sem atrito para transportar telhas do solo até a cobertura de uma residência em obras,
conforme desenho abaixo.
O coeficiente de atrito estático entre a sola do sapato do trabalhador e o chão de concreto é
e
a
massa
de
cada
telha
é
de
2
kg.
μe  1,0
O número máximo de telhas que podem ser sustentadas em repouso, acima do solo, sem que o
trabalhador deslize, permanecendo estático no solo, para um ângulo θ entre a corda e a
horizontal, é:
Aceleração da gravidade : g  10 m / s2
Dados: cos θ  0,8
senθ  0,6
a) 30
b) 25
c) 20
d) 16
e) 10
12. Em um show de patinação no gelo, duas garotas de massas iguais giram em movimento
circular uniforme em torno de uma haste vertical fixa, perpendicular ao plano horizontal. Duas
fitas, F1 e F2, inextensíveis, de massas desprezíveis e mantidas na horizontal, ligam uma garota
à outra, e uma delas à haste. Enquanto as garotas patinam, as fitas, a haste e os centros de
massa das garotas mantêm-se num mesmo plano perpendicular ao piso plano e horizontal.
Considerando as informações indicadas na figura, que o módulo da força de tração na fita F 1 é
igual a 120 N e desprezando o atrito e a resistência do ar, é correto afirmar que o módulo da
força de tração, em newtons, na fita F2 é igual a:
a) 120.
b) 240.
c) 60.
d) 210.
e) 180.
13. Uma estação espacial foi projetada com formato cilíndrico, de raio R igual a 100 m, como
ilustra a figura abaixo.
Para simular o efeito gravitacional e permitir que as pessoas caminhem na parte interna da casca
cilíndrica, a estação gira em torno de seu eixo, com velocidade angular constante ω. As pessoas
terão sensação de peso, como se estivessem na Terra, se a velocidade ω for de,
aproximadamente,
Note e adote: A aceleração gravitacional na superfície da Terra é g = 10 m/s2.
a) 0,1 rad/s
b) 0,3 rad/s
c) 1 rad/s
d) 3 rad/s
e) 10 rad/s
14. A imagem abaixo ilustra uma bola de ferro após ser disparada por um canhão antigo.
Desprezando-se a resistência do ar, o esquema que melhor representa as forças que atuam
sobre a bola de ferro é:
a)
b)
c)
d)
15. Alguns conceitos de física aparecem comumente no cotidiano e são equivocadamente
interpretados. Com relação a esse fato, o conceito correto é o seguinte:
a) calor é energia térmica em trânsito, enquanto temperatura caracteriza a energia térmica de
um sistema em equilíbrio.
b) energia é a medida de uma força atuando sobre um determinado corpo em movimento.
c) massa é a medida de inércia, enquanto peso é a intensidade da força gravitacional.
d) movimento e repouso são consequências da velocidade uniforme de um corpo material.
16. No reino animal, existem seres que têm a capacidade de realizar diferentes tipos de voos.
O voo pode ser dividido em três grupos: o paraquedismo, o planeio e o voo propulsionado. Com
relação aos tipos de voo, considera-se o seguinte:
a) no animal planador, a facilidade do voo depende da forma e da dimensão das asas, sendo o
movimento no ar ascendente e sem realização de trabalho.
b) no paraquedismo, a força de resistência do ar no animal equilibra-se com o seu peso, fazendoo cair com velocidade constante.
c) nos voos propulsionados, os animais exercem a movimentação de seus músculos para
impulsionarem o deslocamento vertical.
d) o paraquedismo e o planeio baseiam-se em princípios físicos iguais, pois as forças de
resistência e peso são um par de ação e reação.
17. Na Amazônia, devido ao seu enorme potencial hídrico, o transporte de grandes cargas é
realizado por balsas que são empurradas por rebocadores potentes. Suponha que se quer
transportar duas balsas carregadas, uma maior de massa M e outra menor de massa m (m<M),
que devem ser empurradas juntas por um mesmo rebocador, e considere a figura abaixo que
mostra duas configurações (A e B) possíveis para este transporte. Na configuração A, o
rebocador exerce sobre a balsa uma força de intensidade F a, e a intensidade das forças
exercidas mutuamente entre as balsas é f a. Analogamente, na configuração B o rebocador
exerce sobre a balsa uma força de intensidade F b, e a intensidade das forças exercidas
mutuamente entre as balsas é fb.
Considerando uma aceleração constante impressa pelo rebocador e desconsiderando quaisquer
outras forças, é correto afirmar que:
a) FA=FB e fa=fb
b) FA>FB e fa=fb
c) FA<FB e fa>fb
d) FA=FB e fa<fb
e) FA=FB e fa>fb
18. Suponha um bloco de massa m = 2 kg inicialmente em repouso sobre um plano horizontal
sem atrito. Uma força F = 16 N é aplicada sobre o bloco, conforme mostra a figura a seguir.
Qual é a intensidade da reação normal do plano de apoio e a aceleração do bloco,
respectivamente, sabendo-se que sen 60° = 0,85, cos 60° = 0,50 e g = 10 m/s2?
a) 6,4 N e 4 m/s2
b) 13, 6 N e 4 m/s2
c) 20,0 N e 8 m/s2
d) 16,0 N e 8 m/s2
e) 8,00 N e 8 m/s2
19. Em um dia sem vento, ao saltar de um avião, um paraquedista cai verticalmente até atingir
a velocidade limite. No instante em que o paraquedas é aberto (instante TA), ocorre a diminuição
de sua velocidade de queda. Algum tempo após a abertura do paraquedas, ele passa a ter
velocidade de queda constante, que possibilita sua aterrissagem em segurança.
Que gráfico representa a força resultante sobre o paraquedista, durante o seu movimento de
queda?
a)
b)
c)
d)
e)
20. Considere um bloco em repouso sobre uma superfície plana, sujeito a uma força externa
horizontal. Por ação gravitacional, esse bloco atua sobre a superfície com uma força de
compressão. A partir das Leis de Newton, o par ação e reação é constituído pelas forças:
a) normal e peso.
b) peso e de atrito.
c) normal e de compressão.
d) externa e de compressão.
21.
Ao analisar a situação representada na tirinha acima, quando o motorista freia subitamente, o
passageiro:
a) mantém-se em repouso e o para-brisa colide contra ele.
b) tende a continuar em movimento e colide contra o para-brisa.
c) é empurrado para frente pela inércia e colide contra o para-brisa.
d) permanece junto ao banco do veículo, por inércia, e o para-brisa colide contra ele.
22. A figura representa dois alpinistas A e B, em que B, tendo atingido o cume da montanha,
puxa A por uma corda, ajudando-o a terminar a escalada. O alpinista A pesa 1 000 N e está em
equilíbrio na encosta da montanha, com tendência de deslizar num ponto de inclinação de 60°
com a horizontal (sen 60° = 0,87 e cos 60° = 0,50); há atrito de coeficiente 0,1 entre os pés de A
e a rocha. No ponto P, o alpinista fixa uma roldana que tem a função exclusiva de desviar a
direção da corda.
A componente horizontal da força que B exerce sobre o solo horizontal na situação descrita, tem
intensidade, em N,
a) 380.
b) 430.
c) 500.
d) 820.
e) 920.
23. Sobre uma superfície sem atrito, há um bloco de massa m 1 = 4,0 kg sobre o qual está
apoiado um bloco menor de massa m 2 = 1,0 kg. Uma corda puxa o bloco menor com uma força
horizontal F de módulo 10 N, como mostrado na figura abaixo, e observa-se que nesta situação
os dois blocos movem-se juntos.
A força de atrito existente entre as superfícies dos blocos vale em Newtons:
a) 10
b) 2,0
c) 40
d) 13
e) 8,0
24. Um jovem aluno de física, atendendo ao pedido de sua mãe para alterar a posição de alguns
móveis da residência, começou empurrando o guarda-roupa do seu quarto, que tem 200 kg de
massa. A força que ele empregou, de intensidade F, horizontal, paralela à superfície sobre a qual
o guarda-roupa deslizaria, se mostrou insuficiente para deslocar o móvel. O estudante solicitou
a ajuda do seu irmão e, desta vez, somando à sua força uma outra força igual, foi possível a
mudança pretendida.
O estudante, desejando compreender a situação-problema vivida, levou-a para sala de aula, a
qual foi tema de discussão. Para compreendê-la, o professor apresentou aos estudantes um
gráfico, abaixo, que relacionava as intensidades da força de atrito (fe, estático, e fc, cinético) com
as intensidades das forças aplicadas ao objeto deslizante.
Com base nas informações apresentadas no gráfico e na situação vivida pelos irmãos, em casa,
é correto afirmar que:
a) o valor da força de atrito estático é sempre maior do que o valor da força de atrito cinético
entre as duas mesmas superfícies.
b) a força de atrito estático entre o guarda-roupa e o chão é sempre numericamente igual ao
peso do guarda-roupa.
c) a força de intensidade F, exercida inicialmente pelo estudante, foi inferior ao valor da força de
atrito cinético entre o guarda-roupa e o chão.
d) a força resultante da ação dos dois irmãos conseguiu deslocar o guarda-roupa porque foi
superior ao valor máximo da força de atrito estático entre o guarda-roupa e o chão.
e) a força resultante da ação dos dois irmãos conseguiu deslocar o guarda-roupa porque foi
superior à intensidade da força de atrito cinético entre o guarda-roupa e o chão.
25. Uma pessoa necessita da força de atrito em seus pés para se deslocar sobre uma superfície.
Logo, uma pessoa que sobe uma rampa em linha reta será auxiliada pela força de atrito exercida
pelo chão em seus pés.
Em relação ao movimento dessa pessoa, quais são a direção e o sentido da força de atrito
mencionada no texto?
a) Perpendicular ao plano e no mesmo sentido do movimento.
b) Paralelo ao plano e no sentido contrário ao movimento.
c) Paralelo ao plano e no mesmo sentido do movimento.
d) Horizontal e no mesmo sentido do movimento.
e) Vertical e sentido para cima.
26. Um avião de acrobacias descreve a seguinte trajetória descrita na figura abaixo:
Ao passar pelo ponto mais baixo da trajetória a força exercida pelo banco da aeronave sobre o
piloto que a comanda é:
a) igual ao peso do piloto.
b) maior que o peso do piloto.
c) menor que o peso do piloto.
d) nula.
e) duas vezes maior do que o peso do piloto.
27. Em um dia muito chuvoso, um automóvel, de massa m, trafega por um trecho horizontal e
circular de raio R. Prevendo situações como essa, em que o atrito dos pneus com a pista
praticamente desaparece, a pista é construída com uma sobre-elevação externa de um ângulo
α , como mostra a figura. A aceleração da gravidade no local é g.
A máxima velocidade que o automóvel, tido como ponto material, poderá desenvolver nesse
trecho, considerando ausência total de atrito, sem derrapar, é dada por:
a) m  g  R  tgα .
b)
m  g  R  cosα .
c)
g  R  tgα .
d)
g  R  cosα .
e)
g  R  senα .
Gabarito:
Resposta
[E]
da
questão
1:
Como a velocidade é constante, de acordo com o princípio da inércia, a resultante das forças é
nula. Então o peso (para baixo) é equilibrado pela soma do empuxo com a força de arrasto (para
cima). Assim: P = E + A.
Resposta
[D]
da
questão
2:
Interpretemos como força, no enunciado, a resultante das forças que agem no objeto.
Considerando trajetória retilínea, do gráfico dado, calculamos a aceleração escalar desse objeto.
Aplicando o Princípio Fundamental da Dinâmica, obtemos o valor algébrico da força resultante,
que é constante no intervalo de tempo mostrado, pois se trata de movimento uniformemente
variado.
a
Δv
-2  6
-8


Δt 2   -2  4
 a  -2 m/s2 .
Fres  m a  5  2   Fres  10 N.
Resposta
[A]
da
questão
3:
A figura mostra as forças que agem sobre o bloco e as componentes do peso.
Na direção paralela ao plano inclinado, a resultante é a componente tangencial do peso.
Aplicando o Princípio Fundamental da Dinâmica:
Px  m a  m g sen θ  m a  a  g sen θ.
Como se pode notar, a intensidade da aceleração independe da massa, tendo o mesmo valor
para a criança e para o adulto. Assim:
aadulto
 1.
acriança
Resposta
[B]
da
questão
4:
 
A resultante das forças sobre o corpo do aspirador é a componente horizontal da força Fx
aplicada no cabo.
Aplicando o Princípio Fundamental da Dinâmica:
 1
Fx  m a  Fcos 60  m a  4    2 a 
2
a  1 m / s2 .
Resposta
[D]
da
questão
5:
Chamemos de A e B os blocos de menor e maior massa, respectivamente. Sendo d a densidade
dos blocos e a a aresta do bloco A, temos:
m  d a3
m
 A
d
 m  d V
 mB  8 m A .
3
3
V
m

d
2
a

8
d
a



 B
Sendo FAB a intensidade da força de contato entre os blocos, aplicando o Princípio Fundamental
da Dinâmica, vem:
F   mA  mB  a  F   mA  8 mA  a  F  9 mA a
 F  9 mA a 

FAB  mB a  FAB  8 mA a
FAB 8 mA a
F
9
 .
FAB 8
Resposta
[A]
da
NOTA: na figura dada, está errada a notação F  750 N.
As formas corretas são: F  750 N ou F = 750 N.
A figura mostra a distribuição de forças pelas polias.
questão
6:
Aplicando o princípio fundamental da dinâmica ao bloco de massa M:
8 F  P  M a  8 750  5.000  500 a  a  2 m/s2.
Calculando a velocidade:
v  v0  a t  v  0  2  2  
Resposta
[E]
v  4 m/s.
da
questão
7:
A velocidade atinge seu valor máximo num ponto entre A e B, quando a peso e a força elástica
têm mesma intensidade.
Resposta
[E]
da
questão
8:
Se a velocidade é nula, a aceleração (a) tem direção tangencial, formando com a vertical ângulo
de 60°, como indicado na figura.
A resultante é a componente tangencial do peso. Aplicando o Princípio Fundamental da
Dinâmica:
 1
Px  m a  m gcos 60  m a  a  10   
2
a  5 m/s2 .
Resposta
[D]
da
questão
9:
[1] Incorreta. A maleta pode ser impedida de se mover pela ação da força de atrito.
[2] Correta. Se a trajetória é retilínea e horizontal, a intensidade (N) da força normal é igual a do
peso (P = m g), e a força resultante sobre a maleta é a força de atrito. Assim, na iminência de a
maleta escorregar:
Fres  m a  μ N  m a  μ m g  m a  a  μ g.
[3] Correta. Como mostrado no item anterior, a aceleração independe da massa, dependendo
apenas do coeficiente de atrito entre o materiais e da intensidade do campo gravitacional local.
Comentário: nas afirmativas [2] e [3] deveria estar especificado que o movimento do avião é
retilíneo e horizontal.
Resposta
[B]
da
questão
10:
No início, a força de atrito (A) é estática e tem valor nulo. À medida que o operário aumenta a
intensidade da força aplicada, a intensidade da força de atrito estática também aumenta, até
atingir o valor máximo (Amáx  μeN), na iminência de escorregamento. Ultrapassado esse valor,
a caixa entra em movimento, a força de atrito passa a ser cinética, constante (Acin  μcN), sendo
Acin  Amáx , pois o coeficiente de atrito cinético é menor que o estático.
Resposta
[B]
da
questão
11:
Dados: M = 70 kg; m = 2 kg;   1,0;
A figura mostra as forças atuantes nas telhas e no trabalhador.
Como se trata de repouso, tanto as forças atuantes no trabalhador como nas telhas estão
equilibradas. Sendo P1 o peso de uma telha e n a quantidade de telhas suspensas, temos:
- Nas telhas:
T  P  n P1  T  n m g.
- No trabalhador:
Fat  Tx  Fat  Tcos   Fat  n m gcos  .



N  Ty  PT  N  M g  T sen   N  M g  n m g sen  .
Na iminência de escorregar, a componente de atrito nos pés do trabalhador atinge intensidade
máxima.
Fatmáx  n m gcos    N  n m gcos  
 M g  n m g sen    n m gcos  
 M g   n m g sen   n m g cos 
 M   n m sen   n mcos   n 
M
m   sen   cos  

1 70
70


2  1 0,8  0,6  2,8
n = 25.
Resposta
[E]
da
questão
12:
A fita F1 impede que a garota da circunferência externa saia pela tangente, enquanto que a fita
F2 impede que as duas garotas saiam pela tangente. Sendo T1 e T2 as intensidades das trações
nas fitas F1 e F2, respectivamente, sendo T1 = 120 N, temos:
T  m ω2 2 R  T  2 m ω2 R  120
 1
1

2
T2  m ω 2 R  m ω2 R  T2  3 m ω2 R

T1 2

T2 3
 T2 
3
3
T1  120  
2
2
T2  180 N.
Resposta
[B]
da
questão
13:
A normal, que age como resultante centrípeta, no pé de uma pessoa tem a mesma intensidade
de seu peso na Terra.
N  Rcent  P  m ω2 R  m g  ω 
g
10
1


r
100
10

ω  0,3 rad/s.
Resposta
[A]
da
questão
14:
Após o lançamento, a única força que age sobre a bola é seu próprio peso, vertical e para baixo.
Resposta
[C]
da
questão
15:
Inércia é a resistência natural que um corpo oferece quando se tenta alterar seu estado de
movimento ou de repouso. A medida da Inércia de um corpo é sua massa. Peso é a força que o
campo gravitacional local aplica no corpo.
Resposta
[B]
da
questão
16:
Pelo Princípio da Inércia, se o animal cai com velocidade constante, a resultante das forças sobre
ele é nula, portanto o peso e força de resistência do ar se equilibram.
Resposta
da
questão
17:
[D]
Sendo M > m, aplicando o Princípio Fundamental da Dinâmica às duas configurações, vem:
FA  M  m  a
A
fa  m a

FB   m  M a
B
fb  M a
FA  FB

fb  fa
Resposta
[A]
da
questão
18:
A figura abaixo mostra as forças que agem no bloco.
As forças verticais anulam-se. Ou seja:
N  Fsen60  P  N  16x0,85  20  N  20  13,6  6,4N
Na horizontal FR  ma  Fcos 60  ma  16x0,5  2a  a  4,0 m/s2
Resposta
[B]
da
questão
19:
No início da queda, a única força atuante sobre o paraquedista (homem + paraquedas) é apenas
o peso [para baixo (+)]. À medida que acelera, aumenta a força de resistência do ar, até que a
resultante se anula, quando é atingida a velocidade limite. No instante (TA) em que o paraquedas
é aberto, a força de resistência do ar aumenta abruptamente, ficando mais intensa que o peso,
invertendo o sentido da resultante [para cima (-)]. O movimento passa a ser retardado até ser
atingida a nova velocidade limite, quando a resultante volta a ser nula.
Resposta
[C]
da
questão
20:
Rigorosamente, não temos par ação-reação em nenhuma das opções.
As forças de ação-reação são da mesma interação, têm mesma direção, mesma intensidade e
sentidos opostos.
As interações realizadas pelo bloco e os respectivos pares de forças de ação-reação geradas,
conforme ilustra a figura, são:
– Bloco-Agente externo: Fext e F'ext .
– Bloco-Terra: P e P'.
– Bloco-Superfície: Fsup e F'sup .
Notemos que a Normal não é uma força, mas apenas uma componente da força que a superfície
troca com o bloco. Caso não houvesse atrito, a força trocada com a superfície seria apenas a
Normal, aí sim teríamos a força de compressão e a Normal formando um par ação-reação.
Resposta
[B]
da
questão
21:
Inércia é uma propriedade de todos os corpos: todo corpo em repouso tende a continuar em
repouso; todo corpo em movimento tende a continuar em movimento retilíneo e uniforme.
Resposta
[D]
da
questão
22:
As figuras mostram as forças agindo no alpinista A na direção da tendência de escorregamento
(x) e direção perpendicular à superfície de apoio (y). No alpinista B, as forças são verticais e
horizontais.
Como os dois estão em repouso, e considerando que o alpinista B esteja na iminência de
escorregar, temos:

T  Fat A  Px A
A 
NA  Py A

 FatB  Px A - Fat A  FatB  PA sen 60   NA 

T  FatB

B 
NB  PB

FatB  PA sen 60   PA cos 60°  FatB  1.000  0,87  0,1 1.000  0,5  870  50 
FatB  820 N.
Resposta
[E]
da
questão
23:
A força F acelera o conjunto.
FR  ma  10  5a  a  2,0m / s2
A força de atrito acelera o bloco de baixo.
Fat  ma  Fat  4x2  8,0N
Resposta
[D]
da
questão
24:
Para haver movimento, a resultante das forças ativas deve ter intensidade maior que a da força
de atrito estática máxima.
Resposta
[C]
da
questão
25:
Quando a pessoa anda, ela aplica no solo uma força de atrito horizontal para trás. Pelo Princípio
da Ação-Reação, o solo aplica nos pés da pessoa uma reação, para frente (no sentido do
movimento), paralela ao solo.
Resposta
[B]
da
questão
26:
Observe a figura abaixo onde estão mostradas as forças que agem no piloto.
Como o movimento é circular deve haver uma força centrípeta apontando para cima. Portanto, a
força da aeronave sobre o piloto deve ser maior que o peso.
Resposta
[C]
da
questão
27:
A figura 1 mostra as forças (peso e normal) agindo nesse corpo. A resultante dessas forças é a
centrípeta (figura 2).
Na figura 2, o triângulo é retângulo:
R
tg   C 
P
v
m v2
R
m g
R g tg  .
 tg  
v2
R g
 v 2  R g tg  