+ + + + + + + + + + + + + - - - - - - - - - - - -

1
Electromagnetismo I
Cursos de Licenciatura em Engenharia Física e em Física - Ramo Científico
Questões teorico-práticas
ano lectivo 2004-2005
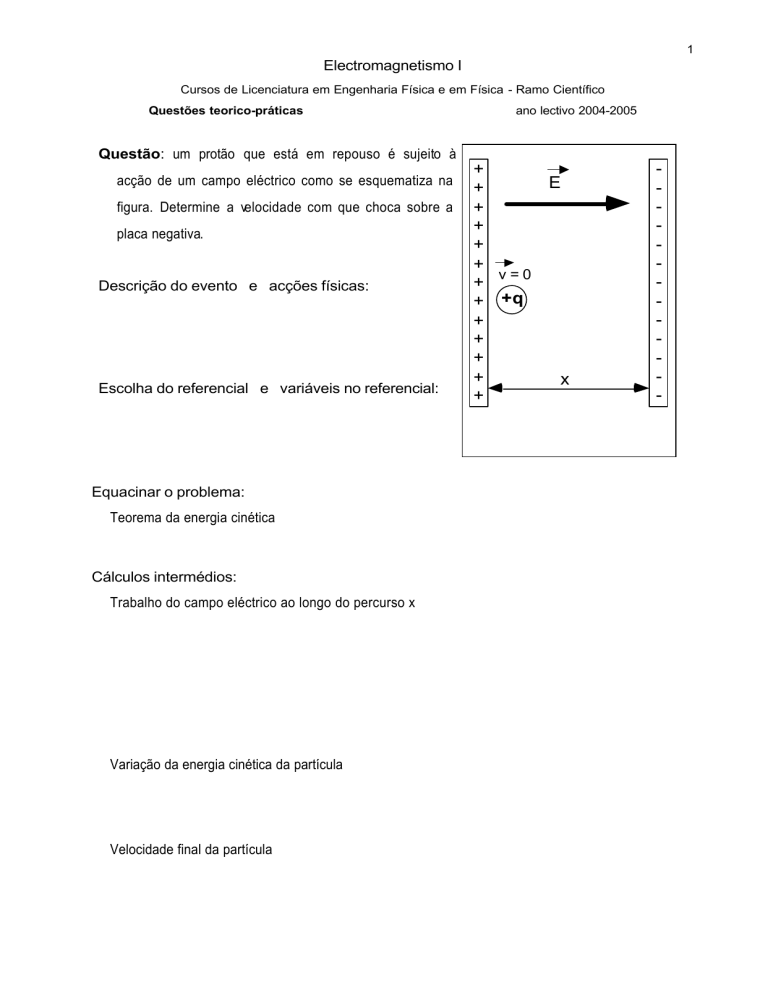
Questão: um protão que está em repouso é sujeito à
acção de um campo eléctrico como se esquematiza na
figura. Determine a velocidade com que choca sobre a
placa negativa.
Descrição do evento e acções físicas:
Escolha do referencial e variáveis no referencial:
Equacinar o problema:
Teorema da energia cinética
Cálculos intermédios:
Trabalho do campo eléctrico ao longo do percurso x
Variação da energia cinética da partícula
Velocidade final da partícula
+
E
+
+
+
+
+
v=0
+
+ +q
+
+
+
+
x
+
-
2
Electromagnetismo I
Cursos de Licenciatura em Engenharia Física e em Física - Ramo Científico
Questões teorico-práticas
ano lectivo 2004-2005
Resposta final
Questão : um electrão deslocase como se esquematiza na figura
impacto com o ecrã.
E
v0
-e
Descrição do evento e
acções físicas:
---------- -l1
Escolha do referencial e variáveis no referencial:
Equacinar o problema:
lei do movimento
lei do movimento
a=
a=
v=
v=
=
=
Cálculos intermédios:
deflexão em l1
deflexão em l2
y2
+++++++++
ao lado. Calcule a sua deflexão no
y1
ecrã
l2
3
Electromagnetismo I
Cursos de Licenciatura em Engenharia Física e em Física - Ramo Científico
Questões teorico-práticas
ano lectivo 2004-2005
Resposta final
Cálculo de campos eléctricos devidos a distribuições contínuas de carga
Densidade de carga: dq =
Aplicação da lei de Coulomb: dE =
Simetria do problema - sistema de coordenadas e variáveis a usar:
Expressão do campo elementar: dE =
Integração sobre toda a distribuição de carga:
4
Electromagnetismo I
Cursos de Licenciatura em Engenharia Física e em Física - Ramo Científico
Questões teorico-práticas
ano lectivo 2004-2005
Operador gradiente em coordenadas esféricas
Para uma carga pontual q
Para um dipolo pontual p
5
Electromagnetismo I
Cursos de Licenciatura em Engenharia Física e em Física - Ramo Científico
Questões teorico-práticas
ano lectivo 2004-2005
Potencial eléctrico devido a distribuições contínuas de carga
Densidade de carga: dq =
Potencial devido a carga pontual: dV =
Sistema de coordenadas e variáveis a usar:
Expressão do potencial devido a carga pontual no referencial e segundo as variáveis definidas:
dV =
Integração sobre toda a distribuição de carga:
V=
6
Electromagnetismo I
Cursos de Licenciatura em Engenharia Física e em Física - Ramo Científico
Questões teorico-práticas
ano lectivo 2004-2005
Utilização da lei de Gauss para o cálculo de campos eléctricos
Exemplo I: Calcule o campo eléctrico que a distribuição da carga Q em todo o volume
de uma esfera de raio R cria em todo o espaço.
As regiões onde se deve calcular o vector E são definidas por:
A distribuição de carga tem simetria ______________________, pelo que a superfície
gaussiana a usar é _____________________ centrado(a) em ___________________
Na superfície escolhida:
- o campo eléctrico é:
- a normal é:
- e o produto escalar:
pelo que o integral de superfície vem:
A carga que está contida dentro da superfície escolhida é:
Usando a lei de Gauss para obter E, tem-se:
Q/e 0
7
Electromagnetismo I
Cursos de Licenciatura em Engenharia Física e em Física - Ramo Científico
Questões teorico-práticas
ano lectivo 2004-2005
Utilização da lei de Gauss para o cálculo de campos eléctricos
Exemplo II: Calcule o campo eléctrico que uma linha infinita com a densidade linear de
carga ? cria em todo o espaço.
As regiões onde se deve calcular o vector E são definidas por:
A distribuição de carga tem simetria ______________________, pelo que a superfície
gaussiana a usar é _____________________ centrado(a) em ___________________
Na superfície escolhida:
- o campo eléctrico é:
- a normal é:
- e o produto escalar:
pelo que o integral de superfície vem:
A carga que está contida dentro da superfície escolhida é:
Usando a lei de Gauss para obter E, tem-se:
Q/e 0
8
Electromagnetismo I
Cursos de Licenciatura em Engenharia Física e em Física - Ramo Científico
Questões teorico-práticas
ano lectivo 2004-2005
Utilização da lei de Gauss para o cálculo de campos eléctricos
Exemplo III: Calcule o campo eléctrico que um plano infinito com a densidade
superficial de carga s cria em todo o espaço.
As regiões onde se deve calcular o vector E são definidas por:
A distribuição de carga tem simetria ______________________, pelo que a superfície
gaussiana a usar é _____________________ centrado(a) em ___________________
Na superfície escolhida:
- o campo eléctrico é:
- a normal é:
- e o produto escalar:
pelo que o integral de superfície vem:
A carga que está contida dentro da superfície escolhida é:
Usando a lei de Gauss para obter E, tem-se:
Q/e 0
9
Electromagnetismo I
Cursos de Licenciatura em Engenharia Física e em Física - Ramo Científico
Questões teorico-práticas
ano lectivo 2004-2005
Condições fronteira do campo electrostático
Problema 1: A figura representa a fronteira de separação
entre dois meios materiais onde existem campos
eléctricos diferentes. Os dois meios têm
diferentes permitividades e1 e e2.
a) Calcule a circulação do campo eléctrico ao longo de
um quadrado localizado junto à fronteira de modo a
que dois dos lados se situem cada um em seu material.
b) Repita o cálculo para a hipótese de o perímetro do
quadrado ser muito reduzido.
c) Considere ainda a hipótese de os lados que
atravessam os dois meios tenderem para zero,
continuando os outros dois em materiais diferentes.
Qual é o valor da circulação do campo eléctrico?
d) Que pode concluir a propósito do campo eléctrico
na fronteira?
a) O integral
Lados
Meio 2
Meio 1
deve considerar 4 lados em que se tem, num plano XY:
1
2
3
4
Ex
Ey
dlx
dly
A circulação do campo eléctrico é:
b) Uma hipótese interessante é a de os 2 lados em cada um dos materiais se reduzirem
de modo a ficarem paralelos à fronteira. Nesse caso:
Lados
Ex
Ey
dlx
dly
1
2
3
4
10
Electromagnetismo I
Cursos de Licenciatura em Engenharia Física e em Física - Ramo Científico
Questões teorico-práticas
ano lectivo 2004-2005
A circulação do campo eléctrico é:
A circulação do campo eléctrico deve ter valor nulo, porque ele é conservativo.
c) No limite em que h tende para zero tem-se:
Lados
1
2
3
4
Ex
Ey
dlx
dly
A circulação do campo eléctrico é:
d) No meio 1 o campo eléctrico é _________________________________________
e tem a grandeza _____________________________.
No meio 2 o campo eléctrico é _________________________________________
e tem a grandeza _____________________________.
Deve concluir-se que
O que se traduz pela equação:
Quanto à componente normal do campo eléctrico, nada se pode concluir.
11
Electromagnetismo I
Cursos de Licenciatura em Engenharia Física e em Física - Ramo Científico
Questões teorico-práticas
ano lectivo 2004-2005
Problema 2: A figura representa a fronteira de separação
entre dois meios materiais onde existem campos
eléctricos diferentes. Os dois meios têm
diferentes permitividades e1 e e2.
a) Calcule o fluxo do vector campo eléctrico que
sai da superfície de um cilindro cujas bases se
situem cada uma em seu material.
b) Repita o cálculo para a hipótese de a área das
bases ser muito reduzida.
c) Considere ainda a hipótese de a altura do
cilindro tender para zero, continuando cada uma
das bases em seu material. Qual é o valor do
fluxo do campo eléctrico? Qual é a carga contida
na superfície fechada?
d) No caso c) use a lei de Gauss para
caracterizar o campo eléctrico na fronteira.
a) O integral
Meio 2
Meio 1
deve considerar 3 superfícies em que se tem, num plano XY:
Superfície
1
2
3
Ex
Ey
dSx
dSy
O fluxo do campo eléctrico é:
b) Uma hipótese interessante é a de as bases em cada um dos materiais se reduzirem
de modo a que a sua normal fique perpendicular à fronteira. Nesse caso:
Superfície
Ex
Ey
dSx
dSy
1
2
3
12
Electromagnetismo I
Cursos de Licenciatura em Engenharia Física e em Física - Ramo Científico
Questões teorico-práticas
ano lectivo 2004-2005
O fluxo do campo eléctrico através da superfície fechada é:
c) No limite em que h tende para zero tem-se:
Superfície
1
2
3
Ex
Ey
dSx
dSy
O fluxo do campo eléctrico é:
A carga contida na superfície fechada fica limitada à carga que se localize sobre a
fronteira de separação dos dois meios:
d) Como se trata de meios de permitividade diferente, é mais cómodo aplicar a lei de
Gauss considerando o vector deslocamento, porque para campo eléctrico havia que
considerar as cargas
_____________ e de ______________. Para o vector
deslocamento apenas se devem considerar as cargas _____________. Tem-se então:
Se existir carga superficial, tem-se:
o que se traduz pela equação:
Se não existir carga superficial, a componente _____________ de ___________ é igual
nos dois materiais; é contínua na superfíce de separação.
Para concluir da componente tangencial do campo eléctrico, há que estudar _______