Gabarito

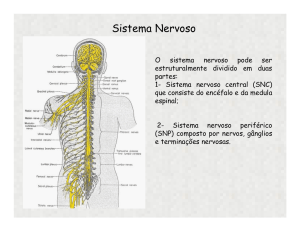
UFCG/CEEI/DSC, Prof. Herman, Redes Neurais 2011.1, Prova1, 24/3/2011 - Gabarito
1) Assinale com um X as características abaixo que não se aplicam a Redes Neurais Artificiais, justificando em
seguida a sua escolha (2.0):
a(X) Pouca generalização. Justificativa: Considerado uso de uma amostra representativa da população para
treinamento e observado um critério de parada (como o uso de um conjunto de validação) que previna o
overfitting, a capacidade de generalização é uma das características mais importantes das redes neurais;
b(X) Aprendizagem realizada a partir de observações simbólicas. Justificativa: na verdade as entradas e saídas de
uma rede neural típica (e.g. MLP) precisam ser necessariamente numéricas.
c(X) Facilidade de expressão do conhecimento adquirido. Justificativa: O conhecimento adquirido é representado
sob a forma de pesos de conexões entre os neurônios da rede. Assim não fica evidente a sua expressão numa
forma inteligível por seres humanos (como por exemplo, regras de decisão).
d( ) Tolerância a falhas.
2) Sobre as redes MLP backpropagation:
(a) Como ocorre a aprendizagem de redes MLP-BP? Procure explicar os passos básicos do algoritmo. Em linhas
gerais, como se pode chegar (formalmente) a esse algoritmo? (2.0)
R:O algoritmo MLP-BP possui 2 passos essenciais que são iterados até que se tenha atingido um critério de
parada do treinamento (como o número máximo de iterações, o máximo erro admissível, dentre outros).
Após inicializada a rede neural com pesos aleatórios pequenos, o primeiro passo (forward) propaga as
entradas de treinamento, camada a camada, efetuando-se os cálculos de ativação dos neurônios (soma
ponderada de pesos por entradas e aplicação da função de ativação) até que se atinja a camada de saída. As
diferenças entre os valores obtidos nos neurônios da camada e os valores das saídas desejadas,
correspondem aos erros da rede neural para aquele padrão de treinamento. No segundo passo (backward)
esses erros são propagados da camada de saída em direção à camada de entrada, ao mesmo tempo em que
os pesos das conexões entre os neurônios são ajustados para minimizar tais erros. Para neurônios na
camada de saída, a regra de atualização considera a derivada da função de ativação, a taxa de aprendizagem
e a diferença entre saída real e desejada (erro). Para neurônios nas camadas escondidas, a fórmula é similar,
mas o erro é calculado como sendo a soma ponderada dos erros estimados na camada seguinte e os pesos
das conexões eferentes daqueles neurônios de camada escondida. A derivação formal de algoritmos de
treinamento para redes neurais usualmente parte da minimização de uma função custo calculada a partir do
erro global associado às unidades de saída e padrões de treinamento.
(b) O que são problemas linearmente separáveis e inseparáveis, e qual a sua relação com redes de Perceptrons?
(1.0)
R:Problemas linearmente separáveis são problemas de classificação de padrões que podem ser resolvidos a
partir de uma superfície de decisão linear. Para os problemas linearmente inseparáveis, não é possível fazer
a separação dos padrões através de uma superfície de decisão linear. Perceptrons de simples camada estão
limitados a resolver problemas linearmente separáveis enquanto que os de múltiplas camadas podem ser
utilizados em problemas linearmente inseparáveis, dado que a propagação dos padrões pelas várias
camadas permite a construção superfícies de decisão que combinam múltiplas superfícies lineares.
3) Qual a importância de incorporar invariâncias ao projeto de Redes Neurais? Escolha e explique 2 das 3
estratégias apresentadas a seguir (2.0). (a) Invariância por estrutura; (b) Invariância por treinamento; (c) Espaços
de características invariantes.
R: A principal importância é simplificar a tarefa de aprendizagem, podendo acelerar a convergência do
treinamento, e aumentar a capacidade de generalização das redes treinadas. (a) Conexões sinápticas entre os
neurônios são definidas de tal forma que versões transformadas de uma mesma entrada são forçadas a produzir
uma mesma saída. (b) Um subconjunto das possíveis transformações que um vetor de entrada pode sofrer é
apresentado durante o treinamento. Uma estratégia muito útil quando é difícil se derivar um modelo para os
dados, porém gera overhead computacional e variações de treinamento precisam ser fornecidas para cada nova
classe. (c) Os padrões de entrada são mapeados em um espaço de características que não sofre grandes
mudanças na presença de variações nos padrões de entrada de uma mesma classe, servindo para redução da
dimensão do espaço de entrada e simplificando a arquitetura da rede neural, porém pode gerar overhead
computacional.
4) Escolha e explique 2 das seguintes potenciais áreas de aplicação das redes neurais artificiais (2.0): a)
Classificação de padrões; b) Agrupamento/categorização; c) Aproximação de funções; d) Previsão; e) Otimização.
R: (a) Objetos do problema (espaço de observação) são descritos através de vetores de características (espaço de
características) os quais, através de um processo de aprendizagem, são mapeados em um conjunto pré-definido
de classes (espaço de decisão). (b) A tarefa é explorar semelhanças entre padrões e agrupar padrões parecidos
numa mesma classe. Também conhecido como aprendizado não supervisionado, uma vez que as classes não são
conhecidas de antemão. (c) O objetivo é encontrar uma aproximação f’ de uma função desconhecida f a partir de
um processo de aprendizagem que recebe como entrada um conjunto de pares de entrada-saída
representativos da função f {(x1y1), (x2y2), ..., (xnyn)}. (d) Dado um conjunto de exemplos {(y(t1), (y(t2),...,
(y(tn)}, a tarefa é prever a saída y(.) no instante de tempo tn+1. (e) A tarefa é encontrar a solução para um
problema que satisfaça a um conjunto de restrições tal que uma função objetivo seja maximizada ou
minimizada.
5) Comente sobre os dados necessários para o treinamento/validação de uma rede neural artificial. Mais
especificamente, discuta o que se pode dizer sobre o tamanho dos dados de treinamento e quantidade de
características, as principais estratégias de pré-processamento, além da necessidade de divisão dos dados em
subconjuntos (1.0).
R: Os dados para o treinamento/validação de uma rede neural artificial precisam ser uma amostra
representativa da população que descreve o problema a ser resolvido. Quanto maior a complexidade de um
problema, maior será a quantidade de dados. Quanto maior o tamanho do vetor de características
representando cada objeto desta amostra, maior precisará ser o tamanho do conjunto de treinamento pois o
espaço de possíveis combinações de valores cresce exponencialmente com o aumento do número de
características de entrada (curse of dimensionality). As principais estratégias de pré-processamento podem ser
resumidas em: conversão de valores simbólicos para valores numéricos; estimativa de valores ausentes e
normalização de valores numéricos. Normalmente, os conjuntos de dados são divididos em subconjuntos de
treinamento/ validação/teste. O primeiro serve para cálculo do erro e ajuste dos pesos entre as unidades. O
segundo, auxilia na decisão de quando parar o treinamento - tipicamente testando se o erro de aproximação do
conjunto de validação atingiu um patamar desejável. O propósito deste critério de parada é evitar o overfitting
ou super especialização da rede neural, que ocorre quando o erro de aproximação do conjunto de treinamento é
muito pequeno, mas perde-se o controle em pontos da função que não estão sendo treinados (dado que
tipicamente uma rede neural representa uma função matemática com muitos parâmetros livres). Por último, o
conjunto de teste serve para avaliar o poder de generalização da rede numa amostra não treinada em função de
sua precisão e taxas de erro. As proporções mais usadas para esses 3 conjuntos são 50, 25 e 25%,
respectivamente.