trabalho potencia e energia

Física Fácil – prof. Erval Oliveira
Aluno:_______________________________
O termo trabalho utilizado na Física difere em
significado do mesmo termo usado no cotidiano.
Fisicamente, um trabalho só é realizado por forças
aplicadas em corpos que se deslocam. Portanto,
deve-se dizer “trabalho realizado pela força aplicada
por pessoas, máquinas etc.” e não “trabalho realizado
por pessoas, máquina etc.”.
serão usadas as notações:
Mas, sabe-se que Ft = F cos  . Portanto, a expressão geral
para o cálculo do trabalho de F constante é:
As unidades de medida mais importantes do trabalho, que
é uma grandeza escalar, são:
TRABALHO DE UMA FORÇA VARIÁVEL
O cálculo do trabalho realizado por uma força de
intensidade variável envolve a utilização de técnicas
matemáticas estudadas em cursos superiores. Para
simplificar, pode-se calcular tal trabalho através da área do
diagrama F x d (intensidade da componente tangencial de F
em função dos valores do deslocamento):
4.
Obs.: a) Trabalho motor é o trabalho realizado por
uma força que favorece o deslocamento do corpo no
qual atua; seu valor é positivo (   0 )
b) Trabalho resistente é o trabalho da força que se
opõe ao deslocamento do corpo no qual age; seu
valor é negativo (   0 ).
2. DEFINIÇÃO MATEMÁTICA DE TRABALHO
Considere-se uma força constante atuando numorpo
que sofre um deslocamento d. Sendo O o ângulo
formado pelos vetores F e d, define-se
matematicamente o trabalho da força F (  F ) como
sendo o produto da intensidade da componente
tangencial de F (F) pela intensidade do deslocamento
(d):
CASOS PARTICULARES
A seguir, serão analisados alguns casos de
realização (ou não) de trabalho por forças diversas.
POTÊNCIA (Pot)
Para se medir a rapidez com que um determinado
trabalho é realizado, define-se uma grandeza escalar
denominada potência.
As unidades de medida de potência são:
GRÁFICO POTÊNCIA X TEMPO
RENDIMENTO
Quando uma máquina está em funcionamento, deve
receber uma determinada potência para que possa
operar. Essa potência é denominada potência total
(Pot). Mas, nos casos reais, a potência total não é
aproveitada inteiramente, dividindo-se em duas
parcelas: a potência útil (Potu) e a potência
dissipada (Potd):
Para que se saiba qual é o aproveitamento que a máquina
(ou um sistema físico) faz da potência total recebida,
define-se o rendimento (  ) através da razão entre as
potências útil e total:
A grandeza escalar expressa por
Ec 
m  v2
é a energia
2
cinética de um corpo em relação a um referencial.
TEOREMA DA ENERGIA CINÉTICA (TEC)
Como foi visto no segmento anterior, o trabalho da força
resultante corresponde à diferença entre os valores final e
inicial da energia cinética.
Note-se que o rendimento é uma grandeza adimensional,
não tendo, portanto, unidade de medida.
Freqüentemente, indica-se o rendimento percentual (i)
multiplicando-se  por 100:
TEC: “O trabalho da força resultante é medido pela
variação da energia cinética.”
ENERGIA POTENCIAL (Ep)
A energia potencial é a energia armazenada num
ENERGIA
Um dos conceitos primitivos mais importantes na
Física é o da energia — uma grandeza escalar que
se manifesta de várias formas no Universo.
A energia relaciona-se diretamente com o trabalho.
Se um sistema físico possui energia, ele é capaz de
realizar
trabalho.
São
conhecidas
diversas
modalidades de energia, conforme a sua natureza:
elétrica, térmica, química, luminosa, nuclear,
mecânica etc., podendo ocorrer transformações
mútuas entre elas.
A energia mecânica é aquela devida a corpos em
movimento (energia cinética) e/ou armazenada em
sistemas físicos (energia potencial).
sistema físico e pode ser transformada em energia
cinética.
Na Mecânica, são consideradas duas formas de
energia potencial: a gravitacional (Epg) e a elástica
(Epe)
ENERGIA CINÉTICA (EJ
Para que um corpo esteja em movimento em relação
a um dado referencial é preciso que haja uma forma
de energia denominada energia cinética.
A expressão para o cálculo dessa energia aparece
num dos mais importantes teoremas da Dinâmica: o
Teorema da Energia Cinética (TEC).
ENERGIA MECÂNICA (Em)
A soma das energias cinética e potencial de um
sistema físico é chamada de energia mecânica:
CONSERVAÇÃO DA ENERGIA MECÂNICA
Nos fenômenos mecânicos, pode-se processar a
transformação entre as energias cinética e potencial.
É importante salientar que, na ausência de forças
dissipativas, a energia mecânica é conservada
(permanece constante), havendo apenas
transformações em suas formas cinética e potencial.
Um sistema físico nestas condições é dito sistema
conservativo.
Desprezando-se as forças dissipativas, como atritos e
resistência do ar, um corpo, durante seu movimento,
apresenta;
Portanto, se a energia mecânica se mantiver
constante durante o movimento de um corpo, em
quaisquer dos pontos de sua trajetória, esta energia
terá o mesmo valor, podendo-se escrever:
Caso haja atrito a variação da energia mecânica será
igual ao trabalho da força de atrito.
5º) Uma preguiça de massa 1,2kg desprende-se do
galho de uma árvore, à beira de um penhasco, e cai
verticalmente. Sua velocidade cresce até 42m/s,
quando se torna constante, devido à resistência do
ar.
2
a) Considerando g = 10m/s , calcule a intensidade
máxima da força de resistência do ar.
b) Em seguida, felizmente, a preguiça cai sobre uma
vegetação arbustiva, que amortece a queda,
parando-a completamente. Calcule a quantidade de
energia mecânica dissipada na interação da preguiça
com a vegetação. (Despreze o trabalho realizado
pela força peso durante o freamento na vegetação.)
EXERCíCIO
1º) Sob a ação de uma força constante, um corpo de
massa m=4,0kg adquire, a partir do repouso, a
velocidade de 10m/s.
a) Qual é trabalho realizado por essa força?
b) Se o corpo se deslocou 25m, qual o valor da força
aplicada?
6º) Uma pedra de 4 kg de massa é colocada em um
ponto A, 10m acima do solo. A pedra é deixada cair
livremente até um ponto B, a 4 m de altura.
Quais são, respectivamente, a energia potencial no
ponto A, a energia potencial no ponto B e o trabalho
realizado sobre a pedra pela força peso? (Use g=10
2
m/s e considere o solo como nível zero para energia
potencial).
a) 40 J, 16 J e 24 J.
b) 40 J, 16 J e 56 J.
c) 400 J, 160 J e 240 J.
d) 400 J, 160 J e 560 J.
e) 400 J, 240 J e 560 J.
2º) Uma criança solta uma pedrinha de massa
m=50g, com velocidade inicial nula, do alto de um
prédio de 100m de altura. Devido ao atrito com o ar, o
gráfico da posição da pedrinha em função do tempo
2
não é mais a parábola y=100-5t , mas sim o gráfico
representado adiante.
7º) Um homem, cuja massa é igual a 80,0 kg, sobe
uma escada com velocidade escalar constante.
Sabe-se que a escada possui 20 degraus e a altura
de cada degrau é de 15,0 cm. DETERMINE a energia
gasta pelo homem para subir toda a escada.
2
Dado: g = 10,0 m/s
 Fat  Emf  Emo
a) Com que velocidade a pedrinha bate no chão
(altura=0)?
b) Qual é o trabalho realizado pela força de atrito
entre t=0 e t=11 segundos?
3º) Uma partícula de massa m=10g se move no plano
x, y com uma velocidade tal que sua componente, ao
longo do eixo x, é de 4,0m/s e, ao longo do eixo y, é
de 2,0m/s. Nessas condições, pode-se afirmar que
sua energia cinética vale:
a) 0,10J. b) 0,18J. c) 100J. d) 180J. e) 190J.
4º) Qual a energia potencial gravitacional de um
corpo de 30kg, que está a 30m acima do solo, em
elação ao próprio solo?
2
Dado que g = 10 m/s .
8º) Um carro recentemente lançado pela indústria
brasileira tem aproximadamente 1500kg e pode
acelerar, do repouso até uma velocidade de 108km/h,
em 10 segundos (fonte: Revista Quatro Rodas,
agosto/92).
Adote 1 cavalo-vapor (CV) = 750 W.
a) Qual o trabalho realizado nesta aceleração?
b) Qual a potência do carro em CV?
9W
9º) Uma hidrelétrica gera 5,0.10 de potência
elétrica utilizando-se de uma queda d'água de 100m.
Suponha que o gerador aproveita 100% da energia
da queda d'água e que a represa coleta 20% de toda
2
a chuva que cai em uma região de 400.000km .
2
Considere que 1 ano tem 32.10§segundos, g=10m/s .
3
a) Qual a vazão de água (m /s) necessária para
9
fornecer os 5,0.10 W?
b) Quantos mm de chuva devem cair por ano nesta
região para manter a hidrelétrica operando nos
9
5,0.10 W?
10º) Uma empilhadeira elétrica transporta do chão
até uma prateleira, a 6m do chão, um pacote de 120
kg. O gráfico adiante ilustra a altura do pacote em
função do tempo. A potência aplicada ao corpo pela
empilhadeira é:
a) 120 W
b) 360 W
c) 720 W
d) 1200 W
e) 2400 W
11º) Um corpo de massa 0,3kg está em repouso num
2
local onde a aceleração gravitacional é 10m/s . A
partir de um certo instante, uma força variável com a
distância segundo a função F=10-20d, onde F(N) e
d(m), passa a atuar no corpo na direção vertical e
sentido ascendente. Qual a energia cinética do corpo
no instante em que a força F se anula?
(Despreze todos os atritos)
a) 1,0J. b) 1,5J. c) 2,0J. d) 2,5J. e) 3,0 J.
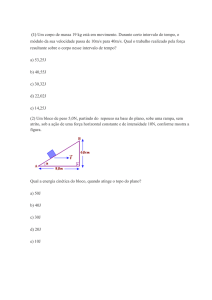
12º) Um pequeno corpo de massa m é abandonado
em A com velocidade nula e escorrega ao longo do
plano inclinado, percorrendo a distância d=AB. Ao
chegar a B, verifica-se que sua velocidade é igual a
Ë(gh). Pode-se então deduzir que o valor da força de
atrito que agiu sobre
o corpo, supondo-a
constante, é
a) zero.
b) mgh.
c) mgh/2.
d) mgh/2d.
e) mgh/4d.
13º) O gráfico a seguir é uma reta e representa a
variação da força resultante que atua em um corpo
de 1,2kg em função do deslocamento. Sabe-se que a
velocidade na
posição x=2m é de
4m/s. Qual é a
velocidade do corpo
na posição x=4m?
a) 10 m/s
b) 6 m/s
c) 8 m/s
d) 16 m/s
e) 9,6 m/s
14º) A figura a seguir ilustra um carrinho de massa m
percorrendo um trecho de uma montanha russa.
Desprezando-se todos os atritos que agem sobre ele
e supondo que o carrinho seja abandonado em A, o
menor valor de h para que o carrinho efetue a
trajetória completa é:
a) (3R)/2
b) (5R)/2
c) 2R
d) 3(5gR)/2
e) 3R
15º) Um bloco de madeira, de massa 0,40kg, mantido
em repouso sobre uma superfície plana, horizontal e
perfeitamente lisa, está comprimindo uma mola
contra uma parede rígida, como mostra a figura a
seguir.
Quando o sistema é liberado, a mola se distende,
impulsiona o bloco e este adquire, ao abandoná-la,
uma velocidade final de 2,0m/s. Determine o trabalho
da força exercida pela
mola, ao se distender
completamente:
a) sobre o bloco e.
b) sobre a parede.
16º) No rótulo de uma lata de leite em pó lê-se:
"Valor energético: 1.509kJ por 100g (361kcal)".
Se toda energia armazenada em uma lata contendo
400g de leite fosse utilizada para levantar um objeto
de 10kg, a altura atingida seria de aproximadamente:
Dado: g=10m/s£
a) 25cm.
b) 15m.
c) 400m.
d) 2km.
e) 60km.
17º) Um carrinho de massa m=300kg percorre uma
montanha russa cujo trecho BCD é um arco de
circunferência de raio R=5,4m, conforme a figura
adiante. A velocidade do carrinho no ponto A é
2
vA=12m/s. Considerando g=10m/s e desprezando o
atrito, calcule;
a) a velocidade do carrinho no ponto C;
b) a aceleração do carrinho no ponto C;
c) a força feita pelos trilhos sobre o carrinho no ponto
C.
18º) Um objeto de massa 400g desce, a partir do
repouso no ponto A, por uma rampa, em forma de um
quadrante de circunferência de raio R=1,0m. Na base
B, choca-se com uma mola de constante elástica
k=200N/m.
Desprezando a ação de forças dissipativas em todo o
2
movimento e adotado g=10m/s , a máxima
deformação da mola é
de
a) 40cm
b) 20cm
c) 10cm
d) 4,0cm
e) 2,0cm