Reconstrução de Imagens - Laboratório de Física Computacional

r.
.D
of
Pr
e
rli
ha
C
M
ni
to
An
lin
ue
iq
Reconstrução de
Imagens
of
Pr
Princípios Básicos
ALGORITMOS!
.D
Conjunto de instruções para gerar um resultado a partir de uma entrada específica.!
r.
rli
ha
C
Em tomografia computadorizada quase todas as instruções são operações
matemáticas.!
TRANSFORMADA DE FOURIER!
e
A transformada de Fourier é uma ferramenta analítica muito utilizada em
matemática, astronomia, química, física e medicina (imagens).!
M
ni
to
An
A compreensão de seu funcionamento tem analogia com a audição.!
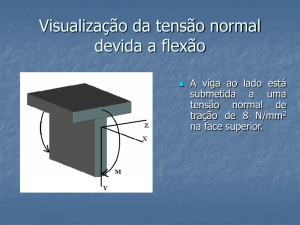
Ela pode ser descrita como sendo uma função que descreve a amplitude e as fases
de senóides, as quais correspondem a uma freqüência específica. !
lin
ue
iq
Esta função converte um conjunto de dados do domínio espacial para o domínio de
frequências.!
A transformada de Fourier divide um sinal em uma série de funções de senos e
cossenos de diferentes freqüências e amplitudes.
of
Pr
Princípios Básicos
r.
.D
O perfil de atenuação em Tomografia Computadorizada pode ser colocado em
termos de uma função f(x) que por sua vez pode ser expressa em forma de uma
Série de Fourier:
a0
+ (a1 ⋅ cos x + b1 ⋅sin x) + (a2 ⋅ cos 2x + b2 ⋅sin 2x) + ...+ (an ⋅ cos nx + bn ⋅sin nx)
2
rli
ha
CONVOLUÇÃO!
C
f (x) =
e
Técnica para modificar imagens através de filtros. Tais filtros são muitas vezes
chamados de kernel.!
M
ni
to
An
O processo envolve a multiplicação de porções sobrepostas do filtro e a curva de
resposta do detetor de maneira seletiva para produzir uma terceira função, que é
utilizada para a reconstrução das imagens.!
INTERPOLAÇÃO!
lin
ue
iq
É usada principalmente na reconstrução de imagens obtidas por equipamentos
helicoidais.!
Técnica matemática para estimar valores de uma função a partir de outros valores
conhecidos desta função.
.D
of
Pr
Reconstrução a partir de projeções
r.
Radon em 1917 desenvolveu soluções
matemática para a construção de imagens a
partir de projeções em problemas
gravitacionais.!
rli
ha
C
e
A aplicação na medicina só veio em 1961 na
reconstrução de imagens em Medicina
Nuclear.!
M
ni
to
An
lin
ue
iq
As primeiras imagens de Hounsfield eram
ruidosas devido ao método de reconstrução.
Posteriormente outros métodos foram
empregados, tendo sido desenvolvidos por
Ramachandran e Lakshiminarayanan (1971)
e posteriormente usados por Sheep e Logan
(1974) para melhorar a qualidade da imagem
e o tempo de aquisição.
Considere um objeto O em
coordenadas x e y e que os
coeficientes de atenuação estão
distribuídos no plano (x,y) sendo
dados por !(x,y).!
r.
.D
of
Pr
O Problema em TC
e
rli
ha
C
I = I 0e
−⎡
⎢⎣
∑ fonte
detetor
μ (x,y) ⎤⎥
⎦
Tomando o logaritmo negativo a
equação anterior pode ser linearizada,
onde Tθ(x) é a transmissão no ângulo
θ, o qual é a medida da absorção total
ao longo da linha reta na figura ao
lado.
lin
ue
iq
detector
I
⎛ ⎞
ln ⎜ 0 ⎟ = ∑ µ (x, y)
⎝ I⎠
fonte
A projeção é dada pela integral de
linha de !(x,y):
M
ni
to
An
⎛ I⎞
Tθ (x) = ln ⎜ ⎟
⎝ I0 ⎠
Um feixe tipo lápis dai de Io e chega
em I formando uma linha reta,
chamada de raio.!
Pr
O Problema em TC
r.
.D
of
Tθ(x) é a chamado também de soma
de raio, que é a integral de !(x,y) ao
longo do raio.!
e
rli
ha
C
O problema computacional em TC é
encontrar os valores de !(x,y) das
somas dos raios para uma número
suficientemente grande de feixes de
localizações conhecidas que passem
através do objeto O. A geometria de
aquisição assegura que cada ponto do
objeto seja irradiado sucessivamente
por um grande conjunto de somas de
raio Tθ(x).!
M
ni
to
An
lin
ue
iq
Um conjunto de somas de raio é
chamada de projeção ou perfil, como
visto na figura ao lado, os quais são
gerados a cada irradiação do sistema
de aquisição de dados. O raio AA’ é
igual a x·cosθ+ y·senθ = d . Neste
caso a projeção é então dada por:
A'
P(θ ,d) = ∫ f (x, y)ds
A
r.
.D
of
Pr
e
rli
ha
C
M
ni
to
An
lin
ue
iq
r.
.D
of
Pr
e
rli
ha
C
M
ni
to
An
lin
ue
iq
r.
.D
of
Pr
e
rli
ha
C
M
ni
to
An
lin
ue
iq
r.
.D
of
Pr
e
rli
ha
C
M
ni
to
An
lin
ue
iq
r.
.D
of
Pr
e
rli
ha
C
M
ni
to
An
lin
ue
iq
r.
.D
of
Pr
e
rli
ha
C
M
ni
to
An
lin
ue
iq
r.
.D
of
Pr
e
rli
ha
C
M
ni
to
An
lin
ue
iq
r.
.D
of
Pr
e
rli
ha
C
M
ni
to
An
lin
ue
iq
r.
.D
of
Pr
Algoritmos de Reconstrução
e
rli
ha
C
Os algoritmos utilizados para
calcular os coeficientes de
atenuação de uma amostra de
dados. A seguir abordaremos os
Algoritmos de Reconstrução mais
conhecidos.!
RETRO-PROJEÇÃO!
M
ni
to
An
Também é conhecido como
método somatório ou método de
superposição linear. É o mais
simples dos métodos de
reconstrução.!
Foi utilizado primeiramente por
Oldendorf (1961) e Kuhl e
Edwards (1963).!
lin
ue
iq
É um método no qual cada
projeção obtida é somada as
demais em função de seu centro de
aquisição.
.D
of
Pr
Algoritmos de Reconstrução
Considere quatro feixes de raios X passando através de um objeto e produzindo quatro
diferentes projeções P1, P2, P3 e P4.!
r.
rli
ha
C
O problema envolve o uso destes perfis para reconstruir a imagem do objeto
desconhecido (buraco) na caixa.!
As projeções são linearmente retroprojetadas em função da direção central em que
forma geradas produzindo as imagens BP1, BP2, BP3, BP4.!
e
M
ni
to
An
A reconstrução por retroprojeção envolve o somatório destas imagens retroprojetadas
para formar uma imagem do objeto original.!
Esta técnica não produz imagens com boa definição e detalhamento das estruturas das
imagens e por isto não é usado em equipamentos de TC de uso clínico.!
lin
ue
iq
O artefato de padrão de estrela é sempre visível na imagem final neste tipo de
reconstrução, isto por que pontos fora do objeto recebem a mesma intensidade
retroprojetada que o próprio objeto.!
A retroprojeção também pode ser explicada por meio de uma matriz 2 x 2.
of
Pr
Algoritmos de Reconstrução
r.
.D
A partir desta matriz quatro
equações são geradas para quatro
variáveis desconhecidas, #1, #2, #3,
e #4.
I 3 = I 0 e−( µ1 + µ3 )⋅x
I 4 = I 0 e−( µ2 + µ4 )⋅x
Estas equações podem ser
re s o l v i d a s f a c i l m e n t e p o r
computadores.!
M
ni
to
An
I 2 = I 0 e−( µ3 + µ4 )⋅x
e
rli
ha
C
I1 = I 0 e−( µ1 + µ2 )⋅x
Um exemplo numérico também
pode ajudar a entender os cálculos
envolvidos.!
lin
ue
iq
Quatro projeções são coletadas em
quatro diferentes localizações: 0,
45, 90 e 135o.
r.
.D
of
Pr
e
rli
ha
C
M
ni
to
An
lin
ue
iq
5
1
r.
.D
of
Pr
e
M
ni
to
An
lin
ue
iq
3
3
rli
ha
C
0
r.
.D
of
Pr
e
rli
ha
M
ni
to
An
4
C
2
lin
ue
iq
r.
.D
of
Pr
e
rli
ha
C
1
2
3
M
ni
to
An
lin
ue
iq
r.
.D
of
Pr
e
rli
ha
M
ni
to
An
4
lin
ue
iq
5
1
3
3
C
10
2
2
3
r.
.D
of
Pr
e
rli
ha
C
M
ni
to
An
lin
ue
iq